四川省泸州市泸县2022_2023学年高二数学下学期期中试题理科含解析

这是一份四川省泸州市泸县2022_2023学年高二数学下学期期中试题理科含解析，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第I卷选择题（60分）
一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 某地区小学，初中，高中三个学段的学生人数分别为4800人，4000人，2400人．现采用分层抽样的方法调查该地区中小学生的“智慧阅读”情况，在抽取的样本中，初中学生人数为70人，则该样本中高中学生人数为（ ）
A. 42人B. 84人C. 126 人D. 196人
【答案】A
【解析】
【分析】设高中抽取人数为，根据条件，建立比例关系进行求解即可．
【详解】解：设高中抽取人数为x
则，得
故选：A
【点睛】本题主要考查了分层抽样应用，属于基础题.
2. 已知复数（i为虚数单位），则z的虚部为（）
A. B. 2C. D.
【答案】A
【解析】
【分析】根据复数的概念及复数的除法即可求解.
【详解】，
所以z的虚部为.
故选：A.
3. 已知命题“，”是假命题，则实数a的取值范围是（）
A. B. （0，4）
C. D.
【答案】C
【解析】
【分析】根据命题与它的否定命题真假性相反，写出该命题的否定命题，再求实数的取值范围．
【详解】解：命题“，”是假命题，
则它的否定命题“，”是真命题，
当时，不等式为，显然成立；
所以时，应满足，解得，
所以实数a的取值范围是．
故选：C．
4. 在的二项展开式中，的系数是（）
A. B. C. D.
【答案】B
【解析】
【分析】写出二项展开式的通项公式令，即得解；
【详解】由题意，二项展开式的通项为：
令因此二项展开式中的系数是：；
故选：B.
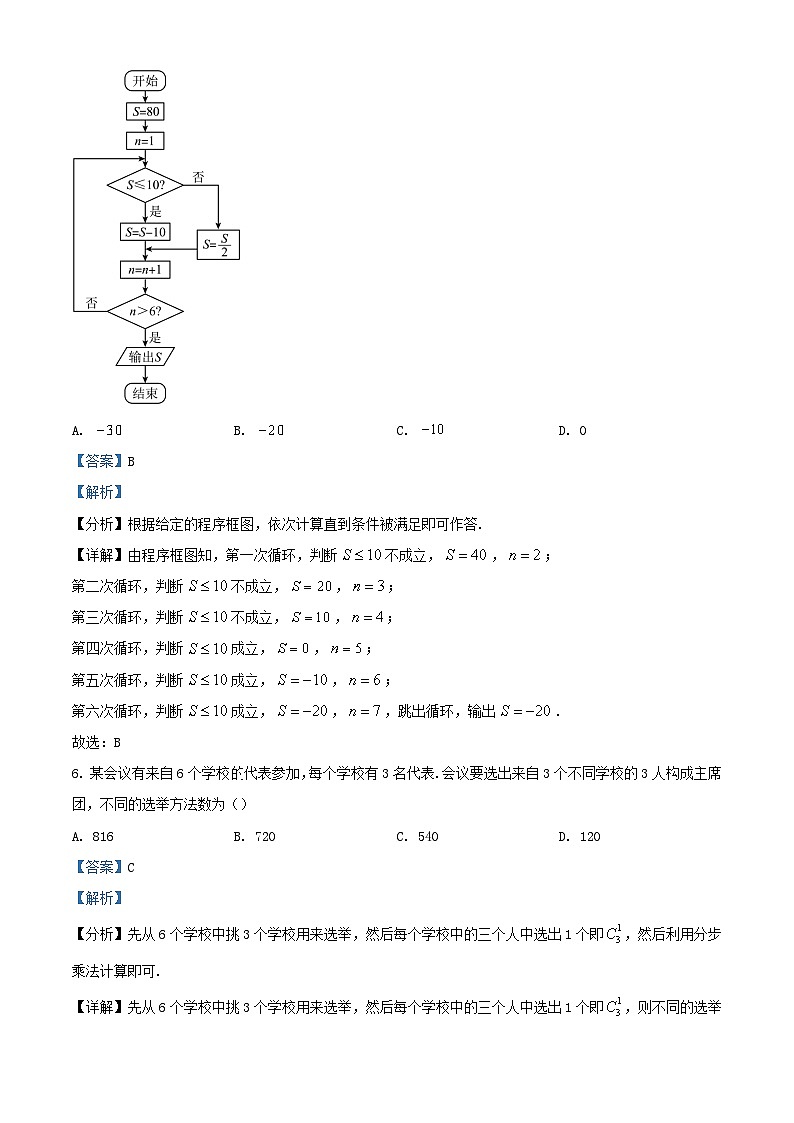
5. 执行如图所示的程序框图，输出的（）
A. B. C. D. 0
【答案】B
【解析】
【分析】根据给定的程序框图，依次计算直到条件被满足即可作答.
【详解】由程序框图知，第一次循环，判断不成立，，；
第二次循环，判断不成立，，；
第三次循环，判断不成立，，；
第四次循环，判断成立，，；
第五次循环，判断成立，，；
第六次循环，判断成立，，，跳出循环，输出．
故选：B
6. 某会议有来自6个学校代表参加，每个学校有3名代表.会议要选出来自3个不同学校的3人构成主席团，不同的选举方法数为（）
A. 816B. 720C. 540D. 120
【答案】C
【解析】
【分析】先从6个学校中挑3个学校用来选举，然后每个学校中的三个人中选出1个即，然后利用分步乘法计算即可.
【详解】先从6个学校中挑3个学校用来选举，然后每个学校中的三个人中选出1个即，则不同的选举方法数为.
故选：C
7. 下表是某厂月份用水量（单位：百吨）的一组数据：
由散点图可知，用水量与月份之间有较好的线性相关关系，其线性回归直线方程是，则
A. B. C. D.
【答案】A
【解析】
【详解】分析：先求出样本中心点，将该点的坐标代入回归方程可求得的值．
详解：由题意得．
∴样本中心为．
∵回归直线过样本中心，
∴，
解得．
故选A．
点睛：回归直线过样本中心是一个重要的结论，利用此结论可求回归直线中的参数，也可求样本数据中的参数．由于此类问题常涉及到大量的运算，所以在解题是要注意计算的准确性．
8. 已知函数，若在区间上单调递减，则实数m的取值范围是（）
A. B. C. D.
【答案】D
【解析】
【分析】首先求得导函数，由原函数单调递增求得函数的单调递增区间，结合题意将原问题转化为子区间的问题，得到关于m的不等式组，求解不等式组即可求得实数m的取值范围.
【详解】详解：因为，
令可得-2≤x≤2，所以要使函数f(x）在区间上单调递减，
则区间（2m，m+1）是区间的子区间，
所以，求解不等式组可得：，
解得-1≤m