【高频真题解析】湖南省邵阳市中考数学备考真题模拟测评 卷（Ⅰ）（含答案及详解）

这是一份【高频真题解析】湖南省邵阳市中考数学备考真题模拟测评 卷（Ⅰ）（含答案及详解），共28页。试卷主要包含了生活中常见的探照灯，利用如图①所示的长为a，下列图形是全等图形的是等内容，欢迎下载使用。
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、和按如图所示的位置摆放，顶点B、C、D在同一直线上，，，．将沿着翻折，得到，将沿着翻折，得，点B、D的对应点、与点C恰好在同一直线上，若，，则的长度为（ ）．
A．7B．6C．5D．4
2、一副三角板按如图所示的方式摆放，则∠1补角的度数为（ ）
A．B．C．D．
3、下列语句中，不正确的是（ ）
A．0是单项式B．多项式的次数是4
C．的系数是D．的系数和次数都是1
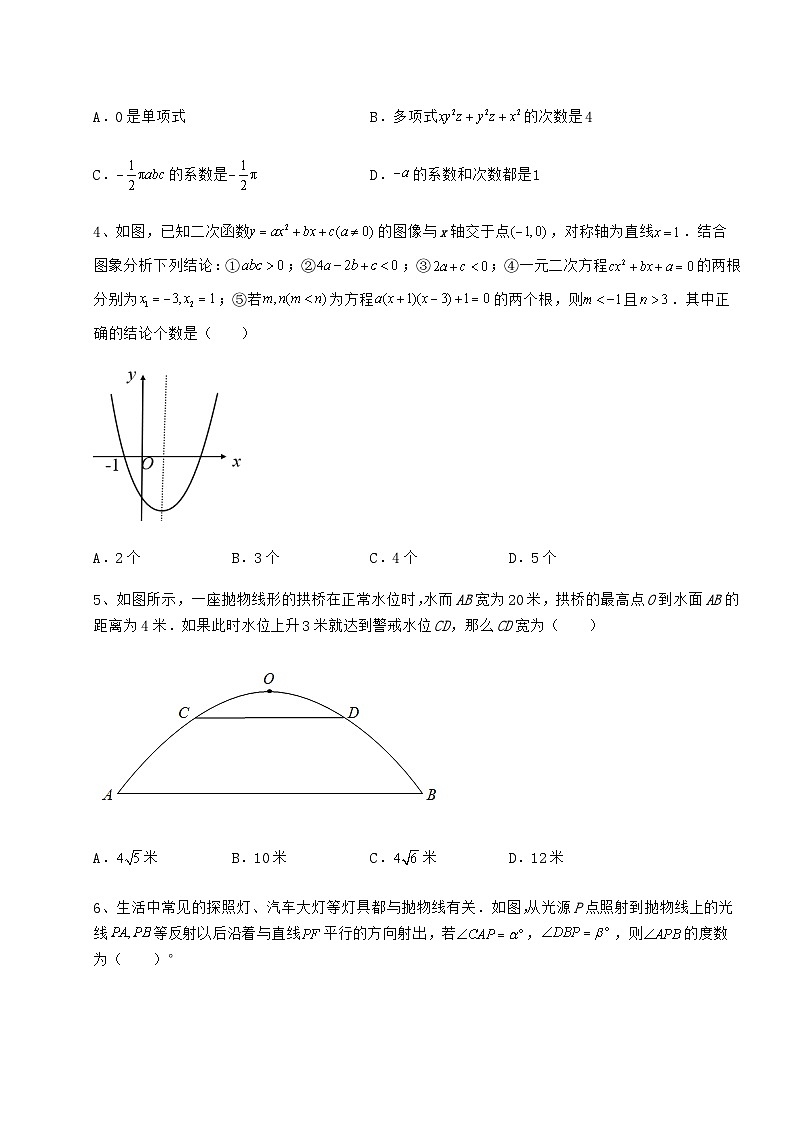
4、如图，已知二次函数的图像与x轴交于点，对称轴为直线．结合图象分析下列结论：①；②；③；④一元二次方程的两根分别为；⑤若为方程的两个根，则且．其中正确的结论个数是（ ）
A．2个B．3个C．4个D．5个
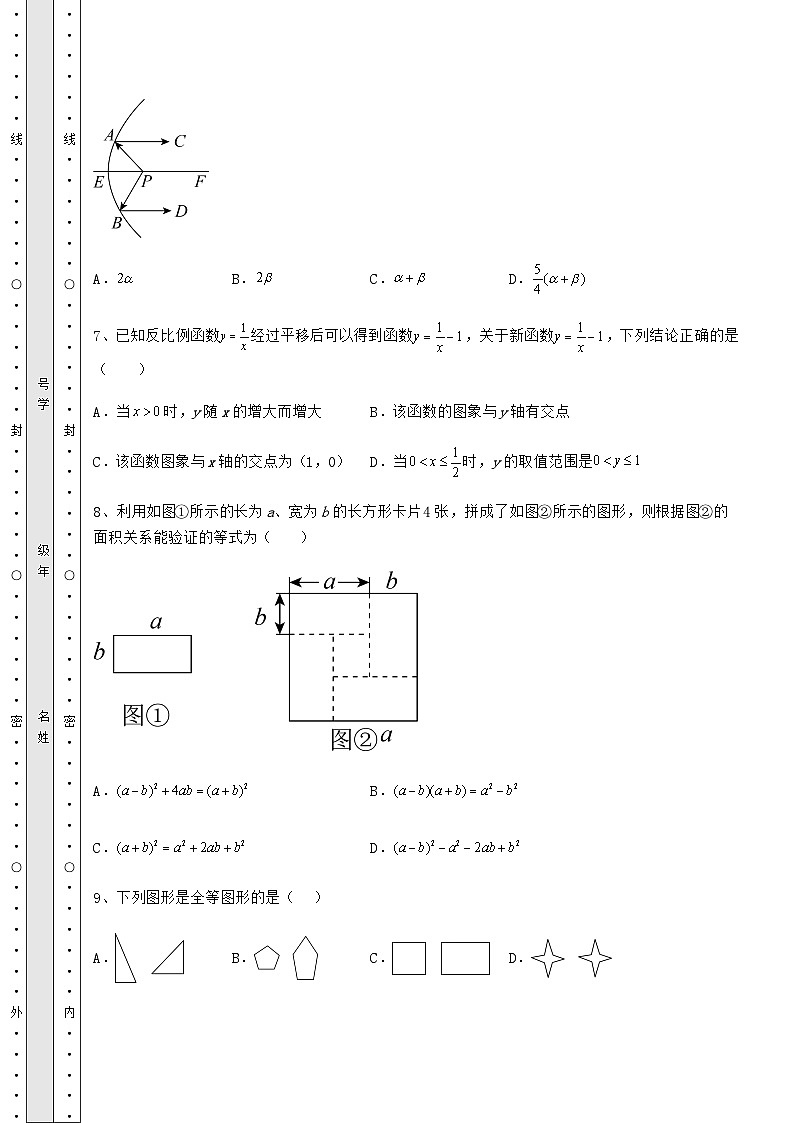
5、如图所示，一座抛物线形的拱桥在正常水位时，水而AB宽为20米，拱桥的最高点O到水面AB的距离为4米．如果此时水位上升3米就达到警戒水位CD，那么CD宽为（ ）
A．米B．10米C．米D．12米
6、生活中常见的探照灯、汽车大灯等灯具都与抛物线有关．如图，从光源P点照射到抛物线上的光线等反射以后沿着与直线平行的方向射出，若，，则的度数为（ ）°
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
A．B．C．D．
7、已知反比例函数经过平移后可以得到函数，关于新函数，下列结论正确的是（ ）
A．当时，y随x的增大而增大B．该函数的图象与y轴有交点
C．该函数图象与x轴的交点为（1，0）D．当时，y的取值范围是
8、利用如图①所示的长为a、宽为b的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的等式为（ ）
A．B．
C．D．
9、下列图形是全等图形的是（ ）
A．B．C．D．
10、东东和爸爸一起出去运动，两人同时从家出发，沿相同路线前行，途中爸爸有事返回，东东继续前行，5分钟后也原路返回，两人恰好同时到家．东东和爸爸在整个运动过程中离家的路程（米），（米）与运动时间（分）之间的函数关系如图所示，下列结论中错误的是（ ）
A．两人前行过程中的速度为180米/分B．的值是15，的值是2700
C．爸爸返回时的速度为90米/分D．运动18分钟或31分钟时，两人相距810米
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、当我们利用两种不同的方法计算同一图形的面积时，可以得到一个等式．例如：由图1可得等式：．
（1）由图2可得等式：________；
（2）利用（1）中所得到的结论，解决下面的问题：已知且，则_______．
2、如图，在中，中线相交于点，如果的面积是4，那么四边形的面积是_________
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
3、在日常生活和生产中有很多现象可以用数学知识进行解释．如图，要把一根挂衣帽的挂钩架水平固定在墙上，至少需要钉______个钉子．用你所学数学知识说明其中的道理______．
4、如图，直角三角形AOB的直角边OA在数轴上，AB与数轴垂直，点O与数轴原点重合，点A表示的实数是2，BA＝2，以点O为圆心，OB的长为半径画弧，与数轴交于点C，则点C对应的数是_____．
5、当a＝﹣1时，代数式2a2﹣a+1的值是 ___．
三、解答题（5小题，每小题10分，共计50分）
1、如图，，，且，，求A点的坐标．
2、如图，已知中，，射线CD交AB于点D，点E是CD上一点，且，联结BE．
（1）求证：
（2）如果CD平分，求证：．
3、（1）探究：如图1，ABCDEF，试说明．
（2）应用：如图2，ABCD，点在、之间，与交于点，与交于点．若，，则的大小是多少？
（3）拓展：如图3，直线在直线、之间，且ABCDEF，点、分别在直线、上，点是直线上的一个动点，且不在直线上，连接、．若，则 度（请直接写出答案）．
4、在数轴上，点A，B分别表示数a，b，且，记．
（1）求AB的值；
（2）如图，点P，Q分别从点A，B；两点同时出发，都沿数轴向右运动，点P的速度是每秒4个单位长度，点Q的速度是每秒1个单位长度，点C从原点出发沿数轴向右运动，速度是每秒3个单位长度，运动时间为t秒．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
①请用含t的式子分别写出点P、点Q、点C所表示的数；
②当t的值是多少时，点C到点P，Q的距离相等？
5、请根据学习“一次函数”时积累的经验和方研究函数的图象和性质，并解决问题．

（1）填空：
①当x＝0时， ；
②当x＞0时， ；
③当x＜0时， ；
（2）在平面直角坐标系中作出函数的图象；
（3）观察函数图象，写出关于这个函数的两条结论；
（4）进一步探究函数图象发现：
①函数图象与轴有 个交点，方程有 个解；
②方程有 个解；
③若关于的方程无解，则的取值范围是 ．
-参考答案-
一、单选题
1、A
【分析】
由折叠的性质得，，故，，推出，由，推出，根据AAS证明，即可得，，设，则，由勾股定理即可求出、，由计算即可得出答案．
【详解】
由折叠的性质得，，
∴，，
∴，
∵，
∴，
∴，
在与中，
，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴，
∴，，
设，则，
∴，
解得：，
∴，，
∴．
故选：A．
【点睛】
本题考查折叠的性质以及全等三角形的判定与性质，掌握全等三角形的判定定理和性质是解题的关键．
2、D
【分析】
根据题意得出∠1=15°，再求∠1补角即可．
【详解】
由图形可得
∴∠1补角的度数为
故选：D．
【点睛】
本题考查利用三角板求度数和补角的定义，熟记各个三角板的角的度数是解题的关键．
3、D
【分析】
分别根据单独一个数也是单项式、多项式中每个单项式的最高次数是这个多项式的次数、单项式中的数字因数是这个单项式的系数、单项式中所有字母的指数和是这个单项式的次数解答即可．
【详解】
解：A、0是单项式，正确，不符合题意；
B、多项式的次数是4，正确，不符合题意；
C、的系数是，正确，不符合题意；
D、的系数是－1，次数是1，错误，符合题意，
故选：D．
【点睛】
本题考查单项式、单项式的系数和次数、多项式的次数，理解相关知识的概念是解答的关键．
4、C
【分析】
根据图像，确定a，b，c的符号，根据对称轴，确定b，a的关系，当x=-1时，得到a-b+c=0，确定a，c的关系，从而化简一元二次方程，求其根即可，利用平移的思想，把y=的图像向上平移1个单位即可，确定方程的根．
【详解】
∵抛物线开口向上，
∴a＞0，
∵抛物线与y轴的交点在y轴的负半轴上，
∴c＜0，
∵抛物线的对称轴在y轴的右边，
∴b＜0，
∴，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
故①正确；
∵二次函数的图像与x轴交于点，
∴a-b+c=0，
根据对称轴的左侧，y随x的增大而减小，
当x=-2时，y＞0即，
故②正确；
∵，
∴b= -2a，
∴3a+c=0，
∴2a+c=2a-3a= -a＜0，
故③正确；
根据题意，得，
∴，
解得，
故④错误；
∵=0，
∴，
∴y=向上平移1个单位，得y=+1，
∴为方程的两个根，且且．
故⑤正确；
故选C．
【点睛】
本题考查了抛物线的图像与系数的符号，抛物线的对称性，抛物线与一元二次方程的关系，抛物线的增减性，平移，熟练掌握抛物线的性质，抛物线与一元二次方程的关系是解题的关键．
5、B
【分析】
以O点为坐标原点，AB的垂直平分线为y轴，过O点作y轴的垂线，建立直角坐标系，设抛物线的解析式为y=ax2，由此可得A（-10，-4），B（10，-4），即可求函数解析式，再将y=-1代入解析式，求出C、D点的横坐标即可求CD的长．
【详解】
以O点为坐标原点，AB的垂直平分线为y轴，过O点作y轴的垂线，建立直角坐标系，
设抛物线的解析式为y=ax2，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∵O点到水面AB的距离为4米，
∴A、B点的纵坐标为-4，
∵水面AB宽为20米，
∴A（-10，-4），B（10，-4），
将A代入y=ax2，
-4=100a，
∴，
∴，
∵水位上升3米就达到警戒水位CD，
∴C点的纵坐标为-1，
∴
∴x=±5，
∴CD=10，
故选：B．
【点睛】
本题考查二次函数的应用，根据题意建立合适的直角坐标系，在该坐标系下求二次函数的解析式是解题的关键．
6、C
【分析】
根据平行线的性质可得，进而根据即可求解
【详解】
解：
故选C
【点睛】
本题考查了平行线的性质，掌握平行线的性质是解题的关键．
7、C
【分析】
函数的图象是由函数的图象向下平移1个单位长度后得到的，根据两个函数的图像，可排除A，B，C选项，将y=0代入函数可得到函数与x轴交点坐标为（1,0），故C选项正确．
【详解】
解：函数与函数的图象如下图所示：
函数的图象是由函数的图象向下平移1个单位长度后得到的，
A、由图象可知函数，当时，y随x的增大而减小，选项说法错误，与题意不符；
B、函数的图象是由函数的图象向下平移一个单位后得到的，所以函数与y轴无交点，· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
选项说法错误，与题意不符；
C、将y=0代入函数中得，，解得，故函数与x轴交点坐标为（1,0），选项说法正确，与题意相符；
D、当时， ，有图像可知当时，y的取值范围是，故选项说法错误，与题意不符；
故选：C．
【点睛】
本题考查反比例函数的图象，以及函数图象的平移，函数与数轴的交点求法，能够画出图象，并掌握数形结合的方法是解决本题的关键．
8、A
【分析】
整个图形为一个正方形，找到边长，表示出面积；也可用1个小正方形的面积加上4个矩形的面积表示，然后让这两个面积相等即可．
【详解】
∵大正方形边长为：，面积为：；
1个小正方形的面积加上4个矩形的面积和为：；
∴．
故选：A．
【点睛】
此题考查了完全平方公式的几何意义，用不同的方法表示相应的面积是解题的关键．
9、D
【详解】
解：A、不是全等图形，故本选项不符合题意；
B、不是全等图形，故本选项不符合题意；
C、不是全等图形，故本选项不符合题意；
D、全等图形，故本选项符合题意；
故选：D
【点睛】
本题主要考查了全等图形的定义，熟练掌握大小形状完全相同的两个图形是全等图形是解题的关键．
10、D
【分析】
两人同行过程中的速度就是20分钟前进3600千米的速度，即可判断A；东东在爸爸返回5分钟后返回即第20分钟返回，即可得到m=15，由此即可计算出n的值和爸爸返回的速度，即可判断B、C；分别求出运动18分钟和运动31分钟两人与家的距离即可得到答案．
【详解】
解：∵3600÷20=180米/分，
∴两人同行过程中的速度为180米/分，故A选项不符合题意；
∵东东在爸爸返回5分钟后返回即第20分钟返回
∴m=20-5=15，
∴n=180×15=2700，故B选项不符合题意；
∴爸爸返回的速度=2700÷（45-15）=90米/分，故C选项不符合题意；
∵当运动18分钟时，爸爸离家的距离=2700-90×（18-15）=2430米，东东离家的距离=180×18=3240米，
∴运动18分钟时两人相距3240-2430=810米；
∵返程过程中东东45-20=25分钟走了3600米，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴东东返程速度=3600÷25=144米/分，
∴运动31分钟时东东离家的距离=3600-144×（31-20）=2016米，爸爸离家的距离=2700-90×（31-15）=1260米，
∴运动31分钟两人相距756米，故D选项符合题意；
故选D．
【点睛】
本题主要考查了从函数图像获取信息，解题的关键在于能够准确读懂函数图像．
二、填空题
1、 2
【解析】
【分析】
（1）方法一：直接利用正方形的面积公式可求出图形的面积；方法二：利用图形的面积等于9部分的面积之和，根据方法一和方法二的结果相等建立等式即可得；
（2）先将已知等式利用完全平方公式、整式的乘法法则变形为，再利用（1）的结论可得，从而可得，由此即可得出答案．
【详解】
解：（1）方法一：图形的面积为，
方法二：图形的面积为，
则由图2可得等式为，
故答案为：；
（2），
，
，
利用（1）的结论得：，
，
，即，
，
，
故答案为：2．
【点睛】
本题考查了完全平方公式与图形面积、整式乘法的应用，熟练掌握完全平方公式和整式的运算法则是解题关键．
2、8
【解析】
【分析】
如图所示，连接DE，先推出DE是△ABC的中位线，得到，DE∥AB，即可证明△ABO∽△DEO，△CDE∽△CBA，得到，从而推出，即可得到，再由，即可得到，由，得到，则．
【详解】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
解：如图所示，连接DE，
∵AD，BE分别是BC，AC边上的中线，
∴D、E分别是BC、AC的中点，
∴DE是△ABC的中位线，
∴，DE∥AB，
∴△ABO∽△DEO，△CDE∽△CBA，
∴，
∴，
∴，
∴，
∴
∵，
∴，
∵，
∴，
∴，
故答案为：8．
【点睛】
本题主要考查了相似三角形的性质与判定，三角形中位线定理，熟知相似三角形的性质与判定条件是解题的关键．
3、 2 两点确定一条直线
【解析】
【分析】
根据两点确定一条直线解答．
【详解】
解：至少需要钉2个钉子，所学的数学知识为：两点确定一条直线，
故答案为：2，两点确定一条直线．
【点睛】
此题考查了线段的性质：两点确定一条直线，熟记性质是解题的关键．
4、
【解析】
【分析】
先利用勾股定理求出，再根据作图过程可得，然后根据实数与数轴的关系即可得．
【详解】
解：由题意得：，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
，
由作图过程可知，，
由数轴的性质可知，点对应的数大于0，
则在数轴上，点对应的数是，
故答案为：．
【点睛】
本题考查了勾股定理、实数与数轴，掌握理解勾股定理是解题关键．
5、4
【解析】
【分析】
把a=-1直接代入2a2-a+1计算即可．
【详解】
解：把a=-1代入2a2-a+1得
2a2-a+1
=2×（-1）2-（-1）+1
=2+1+1
=4；
故答案为：4．
【点睛】
本题考查了代数式的求值，掌握用数值代替代数式里的字母进行计算，正确计算结果是解题关键．
三、解答题
1、A点的坐标为（,）
【分析】
根据题意作AM⊥x轴于M，BN⊥AM于N．只要证明△ABN≌△CAM（AAS），即可推出AM=BN，AN=CM，设OM=a，则CM=5-a，BN=AM=3+a，根据MN=AM-AN，列出方程即可解决问题．
【详解】
解：作AM⊥x轴于M，BN⊥AM于N,
∵∠BAC=90°，
∴∠MAB+∠CAN=90°，
∵∠MAB+∠ABN=90°，
∴∠ABN=∠CAM，
在△ABN和△CAM中，
，
∴△ABN≌△CAM（AAS），
∴AM=BN，AN=CM，
∵，，
设OM=a，则CM=5-a，BN=AM=3+a，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴MN=AM-AN，
5=3+a-（5-a），
∴a=，
∴OM=，AM=，
∴A点的坐标为（,）．
【点睛】
本题考查全等三角形的判定和性质以及平面直角坐标系点的特征，正确作出辅助线构建全等三角形是解题的关键．
2、
（1）见解析；
（2）见解析
【分析】
（1）先根据相似三角形的判定证明△ADE∽△CDB，则可证得即，再根据相似三角形的判定即可证得结论；
（2）根据角平分线定义和相似三角形的性质证明∠DCB=∠EAB=∠EBA=45°，则△AEB为等腰直角三角形，根据勾股定理可得AB2=2BE2，再根据相似三角形的判定证明△EBD∽△ECB即可证得结论．
（1）
证明：∵，∠ADE=∠CDB，
∴△ADE∽△CDB，
∴即，又∠ADC=∠EDB，
∴；
（2）
证明：∵CD平分，∠ACB=90°，
∴∠ACD=∠DCB=45°，
∵△ADE∽△CDB，，
∴∠DCB=∠EAD=∠EBD=45°，
∴AE=BE，∠AEB=90°，
∴△AEB为等腰直角三角形，
∴AB2=AE2+BE2=2BE2，
∵∠DCB =∠EBD，∠CEB =∠BED，
∴△CEB∽△BED，
∴即，
∴AB2=2BE2=2ED·EC．
【点睛】
本题主要考查相似三角形的判定与性质、角平分线的定义、三角形内角和定理、等腰直角三角形的判定、勾股定理，熟练掌握相似三角形的判定与性质是解答的关键．
3、（1）见解析；（2）60°；（3）70或290
【分析】
（1）由可得，，，则；
（2）利用（1）中的结论可知，，则可得的度数为，由对顶角相等可得；
（3）结合（1）中的结论可得，注意需要讨论是钝角或是锐角时两种情况．
【详解】
解：（1）如图1，，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
，，
，
．
（2）由（1）中探究可知，，
，且，
，
；
（3）如图，当为钝角时，
由（1）中结论可知，，
；
当为锐角时，如图，
由（1）中结论可知，，
即，
综上，或．
故答案为：70或290．
【点睛】
本题主要考查平行线的性质与判定，难度适中，观察图形，推出角之间的和差关系是解题关键．
4、
（1）
（2）①点所表示的数为，点所表示的数为，点所表示的数为；②或
【分析】
（1）先根据绝对值的非负性求出的值，再代入计算即可得；
（2）①根据“路程=速度时间”、结合数轴的性质即可得；
②根据建立方程，解方程即可得．
（1）
解：，
，
解得，
；
（2）
解：①由题意，点所表示的数为，
点所表示的数为，
点所表示的数为；
②，，
由得：，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
即或，
解得或，
故当或时，点到点的距离相等．
【点睛】
本题考查了数轴、绝对值、一元一次方程的应用等知识点，熟练掌握数轴的性质是解题关键．
5、（1）2；-x+2，x+2；（2）见解析；（3）函数图象关于y轴对称；当x=0时，y有最大值2；（4）①2 2；②1；③．
【分析】
（1）利用绝对值的意义，分别代入计算，即可得到答案；
（2）结合（1）的结论，画出分段函数的图像即可；
（3）结合函数图像，归纳出函数的性质即可；
（4）结合函数图像，分别进行计算，即可得到答案；
【详解】
解：（1）①当x＝0时，；
②当x＞0时，；
③当x＜0时，；
故答案为：2；x+2；x+2；
（2）函数y＝|x|+2的图象，如图所示：
（3）函数图象关于y轴对称；
当x=0时，y有最大值2．（答案不唯一）
（4）①函数图象与轴有2个交点，方程有2个解；
②方程有1个解；
③若关于的方程无解，则的取值范围是．
故答案为：2；2；1；．
【点睛】
本题考查了一次函数的图像和性质，绝对值的意义，解题的关键是熟练掌握题意，正确的画出图像．