【高频真题解析】湖南省长沙市中考数学真题汇总 卷（Ⅱ）（精选）

这是一份【高频真题解析】湖南省长沙市中考数学真题汇总 卷（Ⅱ）（精选），共27页。试卷主要包含了抛物线的顶点为等内容，欢迎下载使用。
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、下列语句中，不正确的是（ ）
A．0是单项式B．多项式的次数是4
C．的系数是D．的系数和次数都是1
2、下列图形是全等图形的是（ ）
A．B．C．D．
3、如图，有三块菜地△ACD、△ABD、△BDE分别种植三种蔬菜，点D为AE与BC的交点，AD平分∠BAC，AD=DE，AB=3AC，菜地△BDE的面积为96，则菜地△ACD的面积是（ ）
A．24B．27C．32D．36
4、下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
5、整式的值随x取值的变化而变化，下表是当x取不同值时对应的整式的值：
则关于x的方程的解为（ ）
A．B．C．D．
6、如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（ ）
A．75°B．70°C．65°D．55°
7、如图，在平面直角坐标系xOy中，已知点A(1，0)，B(3，0)，C为平面内的动点，且满足∠ACB=90°，D为直线y=x上的动点，则线段CD长的最小值为（ ）
A．1B．2C．D．
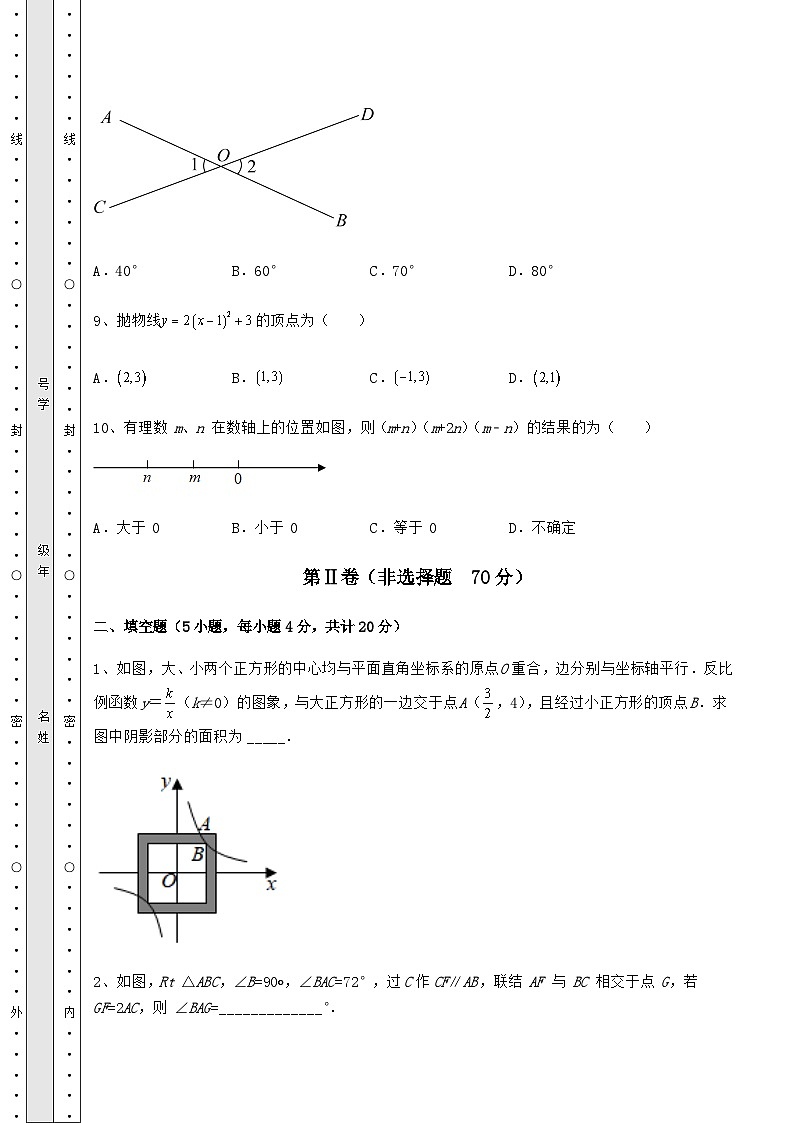
8、如图，直线AB与CD相交于点O，若，则等于（ ）
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
A．40°B．60°C．70°D．80°
9、抛物线的顶点为（ ）
A．B．C．D．
10、有理数 m、n 在数轴上的位置如图，则（m+n）（m+2n）（m﹣n）的结果的为（ ）
A．大于 0B．小于 0C．等于 0D．不确定
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，大、小两个正方形的中心均与平面直角坐标系的原点O重合，边分别与坐标轴平行．反比例函数y＝（k≠0）的图象，与大正方形的一边交于点A（，4），且经过小正方形的顶点B．求图中阴影部分的面积为 _____．
2、如图，Rt △ABC，∠B=90∘，∠BAC=72°，过C作CF∥AB，联结 AF 与 BC 相交于点 G，若 GF=2AC，则 ∠BAG=_____________°．
3、、所表示的有理数如图所示，则________．
4、多项式3x2﹣2xy2+xyz3的次数是 ___．
5、如图，在△ABC中，CD⊥AB，垂足为D，CE为△ACD的角平分线． 若CD=8，BC=10，且△BCE的面积为32，则点E到直线AC的距离为________．
三、解答题（5小题，每小题10分，共计50分）
1、如图，，，且，，求A点的坐标．
2、如图1，在平而直角坐标系中，抛物线（、、为常数，）的图像与轴交· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
于点、两点，与轴交于点，且抛物线的对称轴为直线．
（1）求抛物线的解析式；
（2）在直线上方的抛物线上有一动点，过点作轴，垂足为点，交直线于点；是否存在点，使得取得最大值，若存在请求出它的最大值及点的坐标；若不存在，请说明理由；
（3）如图2，若点是抛物线上另一动点，且满足，请直接写出点的坐标．
3、为庆祝中国共产党建党100周年，某中学开展“学史明理、学史增信、学史崇德、学史力行”知识竞赛，现随机抽取部分学生的成绩按“优秀”、“良好”、“及格”、“不及格”四个等级进行统计，并绘制了如图所示的扇形统计图和条形统计图（部分信息未给出）．根据以上提供的信息，解答下列问题：
（1）本次调查共抽取了多少名学生？
（2）①请补全条形统计图；
②求出扇形统计图中表示“及格”的扇形的圆心角度数．
（3）若该校有2400名学生参加此次竞赛，估计这次竞赛成绩为“优秀”和“良好”等级的学生共有多少名？
4、某演出票价为110元/人，若购买团体票有如下优惠：
例如：200人作为一个团体购票，则需要支付票款元．甲、乙两个班全体学生准备去观看该演出，如果两个班作为一个团体去购票，则应付票款10065元．请列方程解决下列问题：
（1）已知两个班总人数超过100人，求两个班总人数；
（2）在（1）条件下，若甲班人数多于50人．乙班人数不足50人，但至少25人，如果两个班单独购票，一共应付票款11242元．求甲、乙两班分别有多少人？
5、甲、乙两人沿同一直道从A地去B地．已知A，B两地相距9000m，甲的步行速度为100m/min，他每走半个小时就休息15min，经过2小时到达目的地．乙的步行速度始终不变，他在途中不休息，在整个行程中，甲离A地的距离（单位：m）与时间x（单位：min）之间的函数关系如图所示（甲、乙同时出发，且同时到达目的地）．
（1）在图中画出乙离A地的距离（单位：m）与时间x之间的函数图象；
（2）求甲、乙两人在途中相遇的时间．
-参考答案-
一、单选题
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
1、D
【分析】
分别根据单独一个数也是单项式、多项式中每个单项式的最高次数是这个多项式的次数、单项式中的数字因数是这个单项式的系数、单项式中所有字母的指数和是这个单项式的次数解答即可．
【详解】
解：A、0是单项式，正确，不符合题意；
B、多项式的次数是4，正确，不符合题意；
C、的系数是，正确，不符合题意；
D、的系数是－1，次数是1，错误，符合题意，
故选：D．
【点睛】
本题考查单项式、单项式的系数和次数、多项式的次数，理解相关知识的概念是解答的关键．
2、D
【详解】
解：A、不是全等图形，故本选项不符合题意；
B、不是全等图形，故本选项不符合题意；
C、不是全等图形，故本选项不符合题意；
D、全等图形，故本选项符合题意；
故选：D
【点睛】
本题主要考查了全等图形的定义，熟练掌握大小形状完全相同的两个图形是全等图形是解题的关键．
3、C
【分析】
利用三角形的中线平分三角形的面积求得S△ABD=S△BDE=96，利用角平分线的性质得到△ACD与△ABD的高相等，进一步求解即可．
【详解】
解：∵AD=DE，S△BDE=96，
∴S△ABD=S△BDE=96，
过点D作DG⊥AC于点G，过点D作DF⊥AB于点F，
∵AD平分∠BAC，
∴DG=DF，
∴△ACD与△ABD的高相等，
又∵AB=3AC，
∴S△ACD=S△ABD=．
故选：C．
【点睛】
本题考查了角平分线的性质，三角形中线的性质，解题的关键是灵活运用所学知识解决问题．
4、C
【分析】
根据轴对称图形与中心对称图形的概念对各图形分析判断后利用排除法求解．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【详解】
解：
A、不是中心对称图形，是轴对称图形，故此选项错误；
B、是中心对称图形，不是轴对称图形，故此选项错误；
C、是中心对称图形，也是轴对称图形，故此选项正确；
D、不是中心对称图形，是轴对称图形，故此选项错误；
故选：C．
【点睛】
本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．
5、A
【分析】
根据等式的性质把变形为；再根据表格中的数据求解即可．
【详解】
解：关于x的方程变形为，
由表格中的数据可知，当时，；
故选：A．
【点睛】
本题考查了等式的性质，解题关键是恰当地进行等式变形，根据表格求解．
6、B
【分析】
直接根据圆周角定理求解．
【详解】
解：，
．
故选：B．
【点睛】
本题考查了圆周角定理，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
7、C
【分析】
取AB的中点E，过点E作直线y=x的垂线，垂足为D，求出DE长即可求出答案．
【详解】
解：取AB的中点E，过点E作直线y=x的垂线，垂足为D，
∵点A（1，0），B （3，0），
∴OA=1，OB=3，
∴OE=2，
∴ED=2×=，
∵∠ACB=90°，
∴点C在以AB为直径的圆上，
∴线段CD长的最小值为−1．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
故选：C．
【点睛】
本题考查了垂线段最短，一次函数图象上点的坐标特征，圆周角定理等知识，确定C，D两点的位置是解题的关键．
8、A
【分析】
根据对顶角的性质，可得∠1的度数．
【详解】
解：由对顶角相等，得
∠1=∠2，又∠1+∠2=80°，
∴∠1=40°．
故选：A．
【点睛】
本题考查的是对顶角，掌握对顶角相等这一性质是解决此题关键．
9、B
【分析】
根据抛物线的顶点式y=a（x-h）2+k可得顶点坐标是（h，k）．
【详解】
解：∵y=2（x-1）2+3，
∴抛物线的顶点坐标为（1，3），
故选：B．
【点睛】
本题考查二次函数的性质，解题的关键是熟练掌握抛物线的顶点式y=a（x-h）2+k，顶点坐标是（h，k）．
10、A
【分析】
从数轴上看出，判断出，进而判断的正负．
【详解】
解：由题意知：
∴
∴
故选A．
【点睛】
本题考查了有理数加减的代数式正负的判断．解题的关键在于正确判断各代数式的正负．
二、填空题
1、40
【解析】
【分析】
根据待定系数法求出即可得到反比例函数的解析式；利用反比例函数系数的几何意义求出小正方形的面积，再求出大正方形在第一象限的顶点坐标，得到大正方形的面积，根据图中阴影部分的面积大正方形的面积小正方形的面积即可求出结果．
【详解】
解：反比例函数的图象经过点，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
，
反比例函数的解析式为；
小正方形的中心与平面直角坐标系的原点重合，边分别与坐标轴平行，
设点的坐标为，
反比例函数的图象经过点，
，
，
小正方形的面积为，
大正方形的中心与平面直角坐标系的原点重合，边分别与坐标轴平行，且，
大正方形在第一象限的顶点坐标为，
大正方形的面积为，
图中阴影部分的面积大正方形的面积小正方形的面积．
【点睛】
本题主要考查了待定系数法求反比例函数的解析式，反比例函数系数的几何意义，正方形的性质，熟练掌握反比例函数系数的几何意义是解决问题的关键．
2、24
【解析】
【分析】
取FG的中点E，连接EC，根据直角三角形斜边上的中线等于斜边的一半可得EC=AC，从而可推出∠EAC=∠AEC=∠F+∠ECF=2∠F，已知，∠BAC=72°，则不难求得∠BAG的度数．
【详解】
解：如图，取FG的中点E，连接EC．
∵FC∥AB，
∴∠GCF=90°，
∴EC=FG=AC，
∴∠EAC=∠AEC=∠F+∠ECF=2∠F，
设∠BAG=x，则∠F=x，
∵∠BAC=72°，
∴x+2x=72°，
∴x=24°，
∴∠BAG=24°，
故答案为：24．
【点睛】
本题考查了直角三角形斜边上的中线，平行线的性质以及角的计算，解题的关键是构造三个等腰三角形．直角三角形斜边上的中线的性质：直角三角形斜边上的中线等于斜边的一半．
3、
【解析】
【分析】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
根据数轴确定，得出，然后化去绝对值符号，去括号合并同类项即可．
【详解】
解：根据数轴得，
∴，
∴．
故答案为：．
【点睛】
本题考查数轴上点表示数，化简绝对值，整式加减运算，掌握数轴上点表示数，化简绝对值，整式加减运算，关键是利用数轴得出．
4、5
【解析】
【分析】
根据多项式中每个单项式叫做多项式的项，这些单项式中的最高次数，就是这个多项式的次数解答．
【详解】
解：多项式3x2﹣2xy2+xyz3的次数是5．
故答案为：5．
【点睛】
本题考查的是多项式的概念，多项式中每个单项式叫做多项式的项，这些单项式中的最高次数，就是这个多项式的次数．
5、2
【解析】
【分析】
过点E作EF⊥AC于点F，根据角平分线的性质定理可得DE=EF，再由勾股定理可得BD=6，然后根据△BCE的面积为32，可得BE=8，即可求解．
【详解】
解：如图，过点E作EF⊥AC于点F，
∵CE为△ACD的角平分线．CD⊥AB，
∴DE=EF，
在 中，CD=8，BC=10，
∴ ，
∵△BCE的面积为32，
∴ ，
∴BE=8，
∴EF=DE=BE-BD=2，
即点E到直线AC的距离为2．
故答案为：2
【点睛】
本题主要考查了角平分线的性质定理，勾股定理，熟练掌握角平分线的性质定理，勾股定理是解题的关键．
三、解答题
1、A点的坐标为（,）
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【分析】
根据题意作AM⊥x轴于M，BN⊥AM于N．只要证明△ABN≌△CAM（AAS），即可推出AM=BN，AN=CM，设OM=a，则CM=5-a，BN=AM=3+a，根据MN=AM-AN，列出方程即可解决问题．
【详解】
解：作AM⊥x轴于M，BN⊥AM于N,
∵∠BAC=90°，
∴∠MAB+∠CAN=90°，
∵∠MAB+∠ABN=90°，
∴∠ABN=∠CAM，
在△ABN和△CAM中，
，
∴△ABN≌△CAM（AAS），
∴AM=BN，AN=CM，
∵，，
设OM=a，则CM=5-a，BN=AM=3+a，
∴MN=AM-AN，
5=3+a-（5-a），
∴a=，
∴OM=，AM=，
∴A点的坐标为（,）．
【点睛】
本题考查全等三角形的判定和性质以及平面直角坐标系点的特征，正确作出辅助线构建全等三角形是解题的关键．
2、
（1）
（2）；
（3）
【分析】
（1）待定系数法求解析式即可；
（2）过点作于点，求得，直线的解析式为，设，点在直线上，则，进而求得，根据二次函数的性质求得最值以及的值，进而求得的坐标；
（3）取点，连接，则，进而证明，根据的解析式求得的解析式，进而联立抛物线解析式即可求得点的坐标．
（1）
解：抛物线的对称轴为直线，与轴交于点、两点，与轴交于点，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
设抛物线的解析式为，将点代入得
解得
抛物线的解析式为
即
（2）
解：如图，过点作于点，
设直线的解析式为，将点，
代入得：
解得
直线的解析式为
，
是等腰直角三角形
轴，
轴
在中，
在直线上方的抛物线上有一动点，设
点在直线上，则
，
即当时，的最大值为：
此时
即
（3）
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
如图，取点，连接，则，
又
设直线的解析式为
则
解得
直线的解析式为
设直线的解析式为，过点
解得
直线的解析式为
是抛物线上的一点，则为直线与抛物线的交点，则
解得，
【点睛】
本题考查了二次函数综合，一次函数的平移问题，二次函数最值问题，掌握二次函数的图象的性质是解题的关键．
3、
（1）100名
（2）①见解析；②
（3）1440名
【分析】
（1）用不及格的人数除以不及格的人数占比即可得到总人数；
（2）①根据（1）算出的总人数先求出良好的人数，然后求出优秀的人数即可补全统计图；②先求出及格人数的占比，然后用360°乘以及格人数的占比即可得到答案；
（3）先求出样本中，优秀和良好的人数占比，然后估计总体中优秀和良好的人数即可．
（1）
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
解：由题意得抽取的学生人数为：（名）；
（2）
解：①由题意得：良好的人数为：（名），
∴优秀的人数为：（名），
∴补全统计图如下所示：
②由题意得：扇形统计图中表示“及格”的扇形的圆心角度数=；
（3）
解：由题意得：估计这次竞赛成绩为“优秀”和“良好”等级的学生共有（名）．
【点睛】
本题主要考查了条形统计图与扇形统计图信息相关联，画条形统计图，求扇形统计图某一项的圆心角度数，用样本估计总体等等，正确读懂统计图是解题的关键．
4、
（1）人
（2）甲班有人，乙班有人.
【分析】
（1）设两个班总人数为人，再根据各段费用之和为10065元，列方程，再解方程即可；
（2）设乙班有人，则甲班有人，当时，则 再列方程 再解方程可得答案.
（1）
解：设两个班总人数为人，则
整理得：
解得：
答：两个班总人数为人.
（2）
解：设乙班有人，则甲班有人，
当时，则

整理得：
解得：

答：甲班有人，乙班有人.
【点睛】
本题考查的是一元一次方程的应用，最优化选择问题，分段计费问题，理解题意，确定相等关系列方程是解本题的关键.
5、
（1）图象见解析；
（2）甲、乙两人在途中相遇的时间为40分钟，60分钟和80分钟的时候．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【分析】
（1）根据乙的步行速度始终不变，且他在途中不休息，即直接连接原点和点(120，9000)即可；
（2）根据图象可判断甲、乙两人在途中相遇3次，分段计算，利用待定系数法结合图象即可求出相遇的时间．
（1）
乙离A地的距离（单位：m）与时间x之间的函数图像，如图即是．
（2）
根据题意结合图象可知甲、乙两人在途中相遇3次．
如图，第一次相遇在AB段，第二次相遇在BC段，第三次相遇在CD段，
根据题意可设的解析式为：，
∴，
解得：，
∴的解析式为．
∵甲的步行速度为100m/min，他每走半个小时就休息15min，
∴甲第一次休息时走了米，
对于，当时，即，
解得：．
故第一次相遇的时间为40分钟的时候；
设BC段的解析式为：，
根据题意可知B(45，3000)，D (75，6000)．
∴，
解得：，
故BC段的解析式为：．
相遇时即，故有，
解得：．
故第二次相遇的时间为60分钟的时候；
对于，当时，即，
解得：．
故第三次相遇的时间为80分钟的时候；
综上，甲、乙两人在途中相遇的时间为40分钟，60分钟和80分钟的时候．
【点睛】
本题考查一次函数的实际应用．理解题意，掌握利用待定系数法求函数解析式是解答本题的关键．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
x
－1
0
1
2
3
－8
－4
0
4
8
购票人数
不超过50人的部分
超过50人，但不超过100人的部分
超过100人的部分
优惠方案
无优惠
每线票价优惠20%
每线票价优惠50%