2024中考数学二次函数压轴专题训练-专题03最值问题（含解析）

这是一份2024中考数学二次函数压轴专题训练-专题03最值问题（含解析），共29页。
专题03 最值问题
训练题01【2023·浙江杭州·中考真题】
设二次函数是实数，则（ ）
A．当时，函数的最小值为
B．当时，函数的最小值为
C．当时，函数的最小值为
D．当时，函数的最小值为
训练题02【2023·湖北荆州·中考真题】
已知：关于的函数．

(1)若函数的图象与坐标轴有两个公共点，且，则的值是___________；
(2)如图，若函数的图象为抛物线，与轴有两个公共点，，并与动直线交于点，连接，，，，其中交轴于点，交于点．设的面积为，的面积为．
①当点为抛物线顶点时，求的面积；
②探究直线在运动过程中，是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．
训练题03【2022·天津·中考真题】
已知抛物线y＝ax2+bx+c（a，b，c是常数，a＞0）的顶点为P，与x轴相交于点A（﹣1，0）和点B．
（Ⅰ）若b＝﹣2，c＝﹣3，
①求点P的坐标；
②直线x＝m（m是常数，1＜m＜3）与抛物线相交于点M，与BP相交于点G，当MG取得最大值时，求点M，G的坐标；
（Ⅱ）若3b＝2c，直线x＝2与抛物线相交于点N，E是x轴的正半轴上的动点，F是y轴的负半轴上的动点，当PF+FE+EN的最小值为5时，求点E，F的坐标．
训练题04【2023·湖南娄底·中考真题】
如图，抛物线过点、点，交y轴于点C．

(1)求b，c的值．
(2)点是抛物线上的动点,当取何值时，的面积最大？并求出面积的最大值.
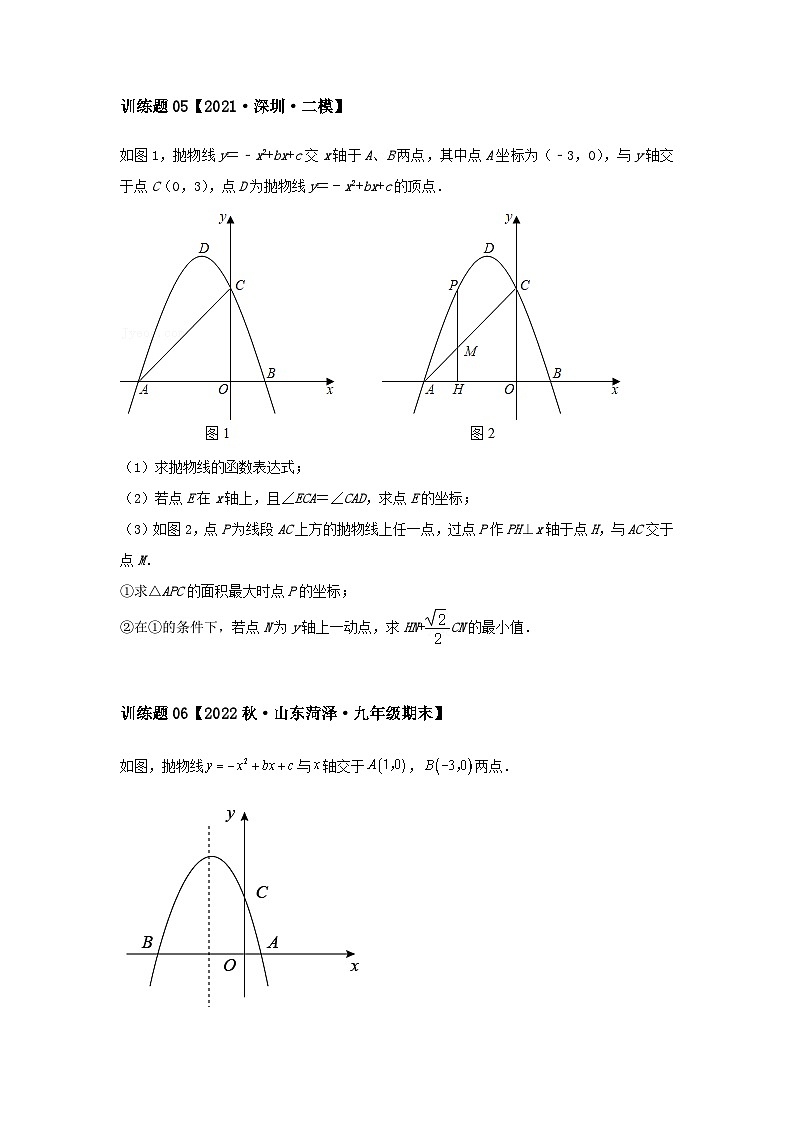
训练题05【2021·深圳·二模】
如图1，抛物线y＝﹣x2+bx+c交x轴于A、B两点，其中点A坐标为（﹣3，0），与y轴交于点C（0，3），点D为抛物线y＝﹣x2+bx+c的顶点．
（1）求抛物线的函数表达式；
（2）若点E在x轴上，且∠ECA＝∠CAD，求点E的坐标；
（3）如图2，点P为线段AC上方的抛物线上任一点，过点P作PH⊥x轴于点H，与AC交于点M．
①求△APC的面积最大时点P的坐标；
②在①的条件下，若点N为y轴上一动点，求HN+CN的最小值．
训练题06【2022秋·山东菏泽·九年级期末】
如图，抛物线与轴交于，两点．
(1)求该抛物线的解析式；
(2)设（1）中的抛物线交轴于点，在该抛物线的对称轴上是否存在点，使得的周长最小？若存在，求出点的坐标；若不存在，请说明理由．
(3)在（1）中的抛物线上的第二象限上是否存在一点，使的面积最大？若存在，求出面积的最大值．若没有，请说明理由．
训练题07【2023·山东聊城·中考真题】
如图①，抛物线与x轴交于点，，与y轴交于点C，连接AC，BC.点P是x轴上任意一点．
(1)求抛物线的表达式；
(2)如图②，当点从点A出发沿x轴向点B运动时（点P与点A，B不重合），自点P分别作，交AC于点E，作，垂足为点D．当m为何值时，面积最大，并求出最大值．
训练题08【2023·浙江·一模】
在平面直角坐标系中，当和时，二次函数（，是常数，）的函数值相等．
(1)若该函数的最大值为，求函数的表达式，并写出函数图象的顶点坐标；
(2)若该函数的图象与轴有且只有一个交点，求，的值．
(3)记（2）中的抛物线为，将抛物线向上平移个单位得到抛物线，当时，抛物线的最大值与最小值之差为，求的值．
训练题09【2023·浙江杭州·滨江期末】
二次函数（为实数，且），对于满足的任意一个的值，都有，则的最大值为（ ）
A．B．C．2D．
训练题10【2023·黑龙江绥化·中考真题】
如图，抛物线的图象经过，，三点，且一次函数的图象经过点．

(1)求抛物线和一次函数的解析式．
(2)将抛物线的图象向右平移个单位长度得到抛物线，此抛物线的图象与轴交于，两点（点在点左侧）．点是抛物线上的一个动点且在直线下方．已知点的横坐标为．过点作于点．求为何值时，有最大值，最大值是多少？
题型训练
答案&解析
训练题01【2023·浙江杭州·中考真题】
【答案】A
【分析】令，则，解得：，，从而求得抛物线对称轴为直线，再分别求出当或时函数y的最小值即可求解．
【详解】解：令，则，
解得：，，
∴抛物线对称轴为直线
当时， 抛物线对称轴为直线，
把代入，得，
∵
∴当，时，y有最小值，最小值为．
故A正确，B错误；
当时， 抛物线对称轴为直线，
把代入，得，
∵
∴当，时，y有最小值，最小值为，
故C、D错误，
故选：A．
训练题02【2023·湖北荆州·中考真题】
【答案】(1)0或2或
(2)①6，②存在，
【分析】（1）根据函数与坐标轴交点情况，分情况讨论函数为一次函数和二次函数的时候，按照图像的性质以及与坐标轴交点的情况即可求出值．
（2）①根据和的坐标点即可求出抛物线的解析式，即可求出顶点坐标，从而求出长度，再利用和的坐标点即可求出的直线解析式，结合即可求出点坐标，从而求出长度，最后利用面积法即可求出的面积．
②观察图形，用值表示出点坐标，再根据平行线分线段成比例求出长度，利用割补法表示出和，将二者相减转化成关于的二次函数的顶点式，利用取值范围即可求出的最小值．
【详解】（1）解：函数的图象与坐标轴有两个公共点，
，
，
，
当函数为一次函数时，，
．
当函数为二次函数时，
，
若函数的图象与坐标轴有两个公共点，即与轴，轴分别只有一个交点时，
，
．
当函数为二次函数时，函数的图象与坐标轴有两个公共点， 即其中一点经过原点，
，，．
综上所述，或0．故答案为：0或2或．
（2）解：①如图所示，设直线与交于点，直线与交于点．

依题意得：，解得：
抛物线的解析式为：．
点为抛物线顶点时，，，
，，
由，得直线的解析式为，
在直线上，且在直线上，则的横坐标等于的横坐标，
，
，，
，
．
故答案为：6．
②存在最大值，理由如下：
如图，设直线交轴于．
由①得：，，，，，
，
，，
，
，
即，
，，
，
，，，当时，有最大值，最大值为．
训练题03【2022·天津·中考真题】
【分析】（Ⅰ）①利用待定系数法求出抛物线的解析式，即可得顶点P的坐标；
②求出直线BP的解析式，设点M（m，m2﹣2m﹣3），则G（m，2m﹣6），表示出MG的长，可得关于m的二次函数，根据二次函数的最值即可求解；
（Ⅱ）由3b＝2c得b＝﹣2a，c＝﹣3a，抛物线的解析式为y＝ax2﹣2a﹣3a．可得顶点P的坐标为（1，﹣4a），点N的坐标为（2，﹣3a），作点P关于y轴的对称点P'，作点N关于x轴的对称点N'，得点P′的坐标为（﹣1，﹣4a），点N'的坐标为（2，3a），当满足条件的点E，F落在直线P'N'上时，PF+FE+EN取得最小值，此时，PF+FE+EN＝P'N'＝5延长P'P与直线x＝2相交于点H，则P'H⊥N'H．在Rt△P'HN'中，P'H＝3，HN'＝3a﹣（﹣4a）＝7a．由勾股定理可得P'N′2＝P'H2+HN2＝9+49a2＝25．解得a1＝，a2＝﹣（舍）．可得点P'的坐标为（﹣1，﹣），点N′的坐标为（2，）．利用待定系数法得直线P'N′的解析式为y＝x﹣．即可得点E，F的坐标．
【详解】解：（Ⅰ）①若b＝﹣2，c＝﹣3，
则抛物线y＝ax2+bx+c＝ax2﹣2x﹣3，
∵抛物线y＝ax2+bx+c与x轴相交于点A（﹣1，0），
∴a+2﹣3＝0，解得a＝1，
∴抛物线为y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴顶点P的坐标为（1，﹣4）；
②当y＝0时，x2﹣2x﹣3＝0，
解得x1＝﹣1，x2＝3，
∴B（3，0），
设直线BP的解析式为y＝kx+n，
∴，解得，
∴直线BP的解析式为y＝2x﹣6，
∵直线x＝m（m是常数，1＜m＜3）与抛物线相交于点M，与BP相交于点G，
设点M（m，m2﹣2m﹣3），则G（m，2m﹣6），
∴MG＝2m﹣6﹣（m2﹣2m﹣3）＝﹣m2+4m﹣3＝﹣（m﹣2）2+1，
∴当m＝2时，MG取得最大值1，
此时，点M（2，﹣3），则G（2，﹣2）；
（Ⅱ）∵抛物线y＝ax2+bx+c与x轴相交于点A（﹣1，0），
∴a﹣b+c＝0，
又3b＝2c，
b＝﹣2a，c＝﹣3a（a＞0），
∴抛物线的解析式为y＝ax2﹣2ax﹣3a．
∴y＝ax2﹣2ax﹣3a＝a（x﹣1）2﹣4a，
∴顶点P的坐标为（1，﹣4a），
∵直线x＝2与抛物线相交于点N，
∴点N的坐标为（2，﹣3a），
作点P关于y轴的对称点P'，作点N关于x轴的对称点N'，
得点P′的坐标为（﹣1，﹣4a），点N'的坐标为（2，3a），
当满足条件的点E，F落在直线P'N'上时，PF+FE+EN取得最小值，此时，PF+FE+EN＝P'N'＝5．
延长P'P与直线x＝2相交于点H，则P'H⊥N'H．
在Rt△P'HN'中，P'H＝3，HN'＝3a﹣（﹣4a）＝7a．
∴P'N′2＝P'H2+HN′2＝9+49a2＝25．
解得a1＝，a2＝﹣（舍）．
∴点P'的坐标为（﹣1，﹣），点N′的坐标为（2，）．
∴直线P'N′的解析式为y＝x﹣．
∴点E（，0），点F（0，﹣）．
训练题04【2023·湖南娄底·中考真题】
【答案】(1)，
(2)当时，的面积由最大值，最大值为
【分析】（1）将将、代入抛物线即可求解；
（2）由（1）可知：，得，可求得的解析式为，过点P作轴，交于点E，交轴于点，易得，根据的面积，可得的面积，即可求解；
【详解】（1）解：将、代入抛物线中，
可得：，解得：，
即：，；
（2）①由（1）可知：，
当时，，即，
设的解析式为：，
将，代入中，
可得，解得：，
∴的解析式为：，
过点P作轴，交于点E，交轴于点，

∵，则，
∴点E的横坐标也为，则纵坐标为，
∴，
的面积
，∵，∴当时，的面积有最大值，最大值为
训练题05【2021·深圳·二模】
【分析】（1）用待定系数法即可求解；
（2）①当点E在点A的左侧时，在Rt△CHN中，NH＝CN＝CH＝，在Rt△AHN中，tan∠HAN＝tan∠DAC＝＝，即tan∠ECA＝tan∠CAD＝，在Rt△CEK中，tan∠ECA＝，进而求解；②当点E（E′）的点A的右侧时，∠ECA＝∠CAD，则直线CE′∥AD，则直线CE′的表达式为y＝2x+3，进而求解；
（3）过点H作HR⊥CG于点R，交CO于点N，则点N为所求点，进而求解．
【详解】解：（1）由题意得：，解得，
故抛物线的表达式为y＝﹣x2﹣2x+3；
（2）①当点E在点A的左侧时，如图1，
由抛物线的表达式知，点D的坐标为（﹣1，4），
延长AD交y轴于点H，过点H作HN交AC的延长线于点N，
由点A、D的坐标得，直线AD的表达式为y＝2（x+3），
故点H的坐标为（0，6），
则CH＝6﹣3＝3，
由点A、C的坐标知，∠ACO＝45°＝∠HCN，AC＝3，
在Rt△CHN中，NH＝CN＝CH＝，
在Rt△AHN中，tan∠HAN＝tan∠DAC＝＝＝，
∴tan∠ECA＝tan∠CAD＝，
过点E作EK⊥CA交CA的延长线于点K，
在Rt△AEK中，∠EAK＝∠CAO＝45°，
故设AK＝EK＝x，则AE＝x，
在Rt△CEK中，tan∠ECA＝＝，
解得x＝，故AE＝x＝3，
则点E的坐标为（﹣6，0）；
②当点E（E′）的点A的右侧时，
∵∠ECA＝∠CAD，
则直线CE′∥AD，
则直线CE′的表达式为y＝2x+r，
而直线CE′过点C，故r＝3，
故直线CE′的表达式为y＝2x+3，
令y＝0，则x＝﹣，
故点E′的坐标为（﹣，0）；
综上，点E的坐标为（﹣6，0）或（﹣，0）；
（3）设点P的坐标为（x，﹣x2﹣2x+3），
由点A、C的坐标得，直线AC的表达式为y＝x+3，
则点M（x，x+3），
则△APC的面积＝×OA×PM＝×3×（﹣x2﹣2x+3﹣x﹣3）＝（﹣x2﹣3x），
∵﹣＜0，故△APC的面积有最大值，
当x＝﹣时，点P的坐标为（﹣，），则点H（﹣，0），
在x轴上取点G（3，0），则OG＝OC，连接CG，
则∠GCO＝45°，
过点H作HR⊥CG于点R，交CO于点N，则点N为所求点，
理由：HN+CN＝HN+CNsin∠GCO＝HN+NR＝HR为最小值，
∵∠CGO＝45°，故△HRG为等腰直角三角形，
则HR＝HG＝（3+）＝，
即HN+CN的最小值为．
训练题06【2022秋·山东菏泽·九年级期末】
【答案】(1)抛物线的解析式为：
(2)存在，点的坐标为
(3)存在，最大值为
【分析】（1）根据题意可知，将点、的坐标代入函数解析式，列出方程组即可求得、的值，求得函数解析式；
（2）根据题意可知，边的长是定值，要想的周长最小，即是最小，所以此题的关键是确定点的位置，找到点的对称点，求得直线的解析式，求得与对称轴的交点即是所求；
（3）设，过点作轴交于点，连接、、，根据，将表示成二次函数，再根据二次函数的性质，即可求得的最大值．
【详解】（1）解：将，代入中，
可得：，
解得：，
∴抛物线的解析式为：；
（2）解：存在，理由如下：
如图，
∵、两点关于抛物线的对称轴对称，
∴直线与的交点即为点，此时周长最小，连接、，
∵点是抛物线与轴的交点，
∴的坐标为，
又∵，
∴直线解析式为：，
∴点坐标即为，
解得：，
∴；
（3）解：存在，理由如下：
如图，设，过点作轴交于点，连接、、，
∵，
若有最大值，则就最大，
∴，
∵，
又∵，
∴，
∴，
∴，
∴当时，最大值为．
训练题07【2023·山东聊城·中考真题】
【答案】(1)
(2)时，有最大值，最大值为．
【分析】（1）将，代入，待定系数法确定函数解析式；
（2）如图，过点D作，过点E作，垂足为G，F，
可证，；运用待定系数法求直线解析式，直线 解析式；设点，，则，，，，运用解直角三角形，中，，，中，，可得，，；中，，可得，，，，于是，从而确定时，最大值为．
【详解】（1）将，代入，得，解得
∴抛物线解析式为：
（2）如图，过点D作，过点E作，垂足为G，F，
∵，
∴
∴
∵
∴，同理可得
设直线的解析式为：
则，解得
∴直线：
同理由点，，可求得直线 ：
设点，，
则，，，
中，，
∴，
中，
∴，解得，
∴
∵
∴；
中，
∴，解得，
∴
∵
∴
∴，
即．
∵，∴时，，有最大值，最大值为．
训练题08【2023·浙江·一模】
【答案】(1)，；
(2)，；
(3)．
【分析】（1）根据二次函数的性质及对称轴即可解答；
（2）根据二次函数与轴的交点个数及二次函数的性质即可解答；
（3）根据二次函数的平移规律及二次函数的性质即可解答．
【详解】（1）解：∵当和时，二次函数（，是常数，）的函数值相等，
∴二次函数的对称轴为，，
∵该函数的最大值为，
∴该函数的顶点坐标为，
∴，
∴由①②可得：，
∴函数表达式为：；
（2）解：∵该函数的图象与轴有且只有一个交点，
∴一元二次方程，该函数的顶点坐标为，
∴，，
∴由①②可得（舍去），，
∴，；
（3）解：由（2）可得的解析式为：，
∵将抛物线向上平移个单位得到抛物线，
∴，
∴当时，，
∵的顶点坐标为，且当时，抛物线的最大值与最小值之差为，
∴，随的增大而增大，
∴，
∴，
∴，
∴，
∵，
∴．
训练题09【2023·浙江杭州·滨江期末】
【答案】D
【分析】由该二次函数解析式可知，该函数图像的开口方向向下，对称轴为，该函数的最大值为，由题意可解得，根据函数图像可知的值越小，其对称轴越靠左，满足的的值越小，故令即可求得的最大值．
【详解】解：∵函数，且，
∴该函数图像的开口方向向下，对称轴为，该函数有最大值，其最大值为，
若要满足的任意一个的值，都有，
则有，解得，
对于该函数图像的对称轴，
的值越小，其对称轴越靠左，如下图，
结合图像可知，的值越小，满足的的值越小，
∴当取的最大值，即时，令，
解得，，
∴满足的的最大值为，
即的最大值为．
故选：D．
训练题10【2023·黑龙江绥化·中考真题】
【答案】(1)，
(2)当时，的最大值为
【分析】（1）待定系数法求解析式即可求解；
（2）得出是等腰直角三角形，是等腰直角三角形，则，点在抛物线上，且横坐标为得出，进而可得，则，根据二次函数的性质即可求解．
【详解】（1）解：把，，代入
得 ，解得
∴
把代入得
∴
（2）∵向右平移8个单位长度得到抛物线
当，即
解得：
∴，
∵过，，三点
∴
在直线下方的抛物线上任取一点，作轴交于点，过点作轴于点

∵，
∴
∴是等腰直角三角形
∵，
∴
又
∴是等腰直角三角形
∴
∵点在抛物线上，且横坐标为
∴
∴
∵
∴
∴
∴
∴
∴当时，的最大值为．