2024中考数学二次函数压轴专题训练-专题06圆相关问题（含解析）

这是一份2024中考数学二次函数压轴专题训练-专题06圆相关问题（含解析），共33页。
专题06 圆相关问题
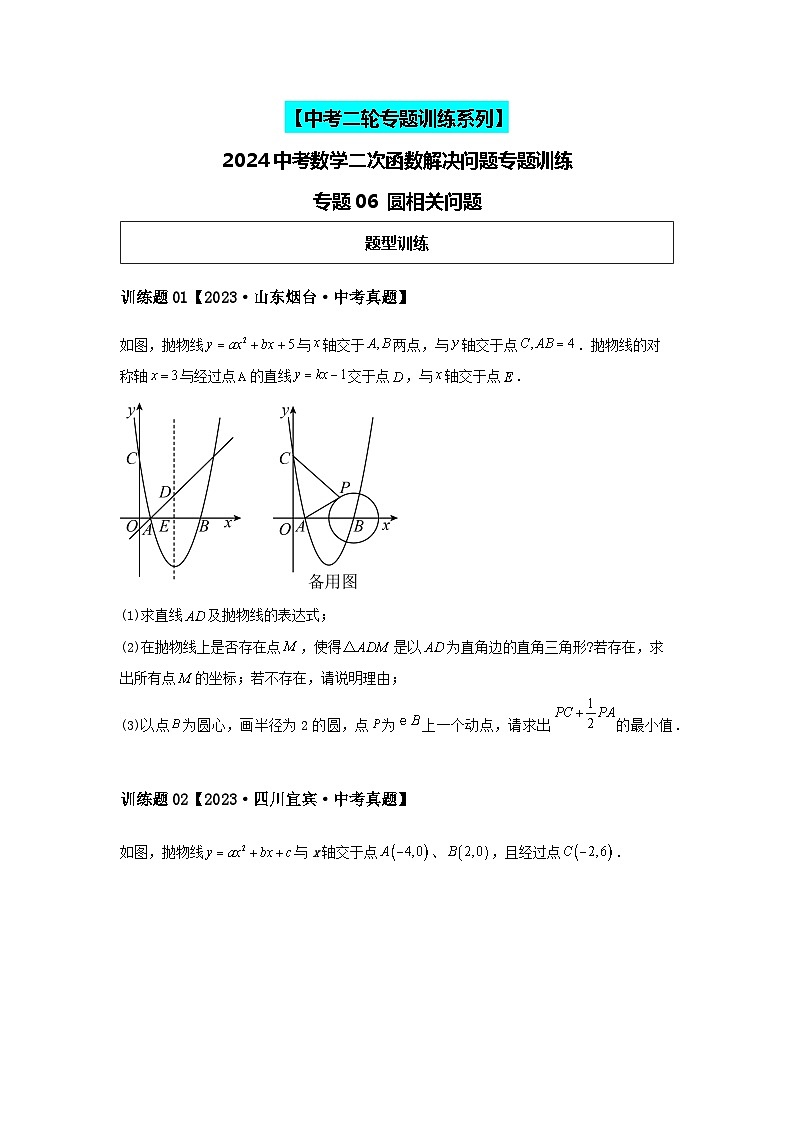
训练题01【2023·山东烟台·中考真题】
如图，抛物线与轴交于两点，与轴交于点．抛物线的对称轴与经过点的直线交于点，与轴交于点．

(1)求直线及抛物线的表达式；
(2)在抛物线上是否存在点，使得是以为直角边的直角三角形?若存在，求出所有点的坐标；若不存在，请说明理由；
(3)以点为圆心，画半径为2的圆，点为上一个动点，请求出的最小值．
训练题02【2023·四川宜宾·中考真题】
如图，抛物线与x轴交于点、，且经过点．

(1)求抛物线的表达式；
(2)在x轴上方的抛物线上任取一点N，射线、分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为，求的面积；
(3)点M是y轴上一动点，当最大时，求M的坐标．
训练题03【2023·湖南怀化·中考真题】
如图一所示，在平面直角坐标系中，抛物线与轴交于两点，与轴交于点．

(1)求抛物线的函数表达式及顶点坐标；
(2)设直线交抛物线于点、，求证：无论为何值，平行于轴的直线上总存在一点，使得为直角．
训练题04【2023·江苏无锡·统考三模】
如图，抛物线与x轴交于点．

(1)求抛物线的函数表达式；
(2)点是抛物线上一点，点C是线段上一点，连接并延长交抛物线于点D，若，求点D的坐标；
(3)抛物线上是否存在点P，使得？若存在，求出点P的坐标：若不存在，说明理由．
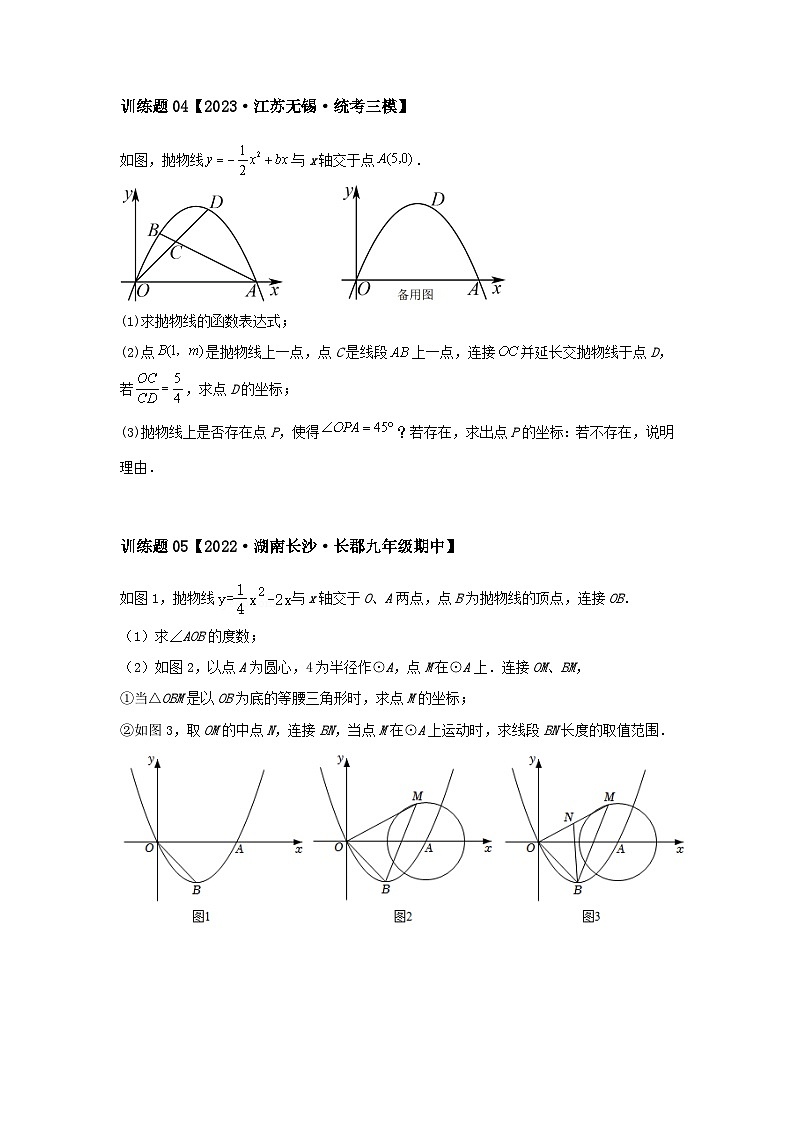
训练题05【2022·湖南长沙·长郡九年级期中】
如图1，抛物线与x轴交于O、A两点，点B为抛物线的顶点，连接OB．
（1）求∠AOB的度数；
（2）如图2，以点A为圆心，4为半径作⊙A，点M在⊙A上．连接OM、BM，
①当△OBM是以OB为底的等腰三角形时，求点M的坐标；
②如图3，取OM的中点N，连接BN，当点M在⊙A上运动时，求线段BN长度的取值范围．
训练题06【2022·浙江嘉兴·统考二模】
定义：平面直角坐标系xOy中，过二次函数图象与坐标轴交点的圆，称为该二次函数的坐标圆．
（1）已知点P（2，2），以P为圆心，为半径作圆．请判断⊙P是不是二次函数y＝x2﹣4x+3的坐标圆，并说明理由；
（2）已知二次函数y＝x2﹣4x+4图象的顶点为A，坐标圆的圆心为P，如图1，求△POA周长的最小值；
（3）已知二次函数y＝ax2﹣4x+4（0＜a＜1）图象交x轴于点A，B，交y轴于点C，与坐标圆的第四个交点为D，连结PC，PD，如图2．若∠CPD＝120°，求a的值．
训练题07【2023·江苏苏州·统考一模】
如图，二次函数y=-14x2+12m-1x+m（m是常数，且m>0）的图象与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，动点P在对称轴l上，连接AC、BC、PA、PC．
(1)求点A、B、C的坐标（用数字或含m的式子表示）；
(2)当PA+PC的最小值等于45时，求m的值及此时点P的坐标；
(3)当m取（2）中的值时，若∠APC=2∠ABC，请直接写出点P的坐标．
训练题08【2021·甘肃兰州·中考真题】
二次函数的图象交轴于两点，交轴于点.动点从点出发，以每秒2个单位长度的速度沿方向运动，过点作轴交直线于点，交抛物线于点，连接.设运动的时间为秒.
(1)求二次函数的表达式:
(2)当时，在直线上存在一点，使得，求点的坐标
训练题09【2022·福建·统考模拟】
如图，已知抛物线y＝ax2+bx+c与x轴相交于A，B两点，点C（2，﹣4）在抛物线上，且△ABC是等腰直角三角形．
（1）求抛物线的解析式；
（2）过点D（2，0）的直线与抛物线交于点M，N，试问：以线段MN为直径的圆是否过定点？证明你的结论．
训练题10【2022·上海闵行·二模】
如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+4与x轴相交于点A（﹣1，0），B（3，0），与y轴交于点C．将抛物线的对称轴沿x轴的正方向平移，平移后交x轴于点D，交线段BC于点E，交抛物线于点F，过点F作直线BC的垂线，垂足为点G．
（1）求抛物线的表达式；
（2）以点G为圆心，BG为半径画⊙G；以点E为圆心，EF为半径画⊙E．
当⊙G与⊙E内切时．
①试证明EF与EB的数量关系；
②求点F的坐标．
题型训练
答案&解析
训练题01【2023·山东烟台·中考真题】
【答案】(1)直线的解析式为；抛物线解析式为
(2)存在，点M的坐标为或 或
(3)
【分析】（1）根据对称轴，，得到点A及B的坐标，再利用待定系数法求解析式即可；
（2）先求出点D的坐标，再分两种情况：①当时，求出直线的解析式为y=-x+1 ，解方程组y=-x+1y=x2-6x+5，即可得到点M的坐标；②当时，求出直线的解析式为，解方程组，即可得到点M的坐标；
（3）在上取点，使，连接，证得，又，得到，推出，进而得到当点C、P、F三点共线时，的值最小，即为线段的长，利用勾股定理求出即可．
【详解】（1）解：∵抛物线的对称轴，，
∴，
将代入直线，得，
解得，
∴直线的解析式为；
将代入，得
，解得，
∴抛物线的解析式为；
（2）存在点，
∵直线的解析式为，抛物线对称轴与轴交于点．
∴当时，，
∴，
①当时，
设直线的解析式为，将点A坐标代入，
得，
解得，
∴直线的解析式为y=-x+1，
解方程组，
得或，
∴点M的坐标为；
②当时，
设直线的解析式为，将代入，
得，
解得，
∴直线的解析式为，
解方程组，
解得或，
∴点M的坐标为 或
综上，点M的坐标为或 或；
（3）如图，在上取点，使，连接，
∵，
∴，
∵，、
∴，
又∵，
∴，
∴，即，
∴，
∴当点C、P、F三点共线时，的值最小，即为线段的长，
∵，
∴，
∴的最小值为．

训练题02【2023·四川宜宾·中考真题】
【答案】(1)
(2)
(3)
【分析】（1）设抛物线的解析式为，代入点C的坐标，确定a值即可．
（2）设，直线的解析式为，直线的解析式为，表示出P，Q，的坐标，进而计算即可．
（3）当M是y轴与经过A，C，M三点的圆的切点是最大计算即可.
【详解】（1）∵抛物线与x轴交于点、，
∴设抛物线的解析式为，
∵经过点，
∴，
解得，
∴，
∴．
（2）如图，当点N在对称轴的右侧时，
∵，
∴对称轴为直线，

设，直线的解析式为，直线的解析式为，
∴
解得，
∴直线的解析式为，直线的解析式为，
当时，，
，
∴，，，
∴，
∴．
如图，当点N在对称轴的左侧时，
∵，
∴对称轴为直线，

设，，，，
∴，
∴．
综上所述，．
（3）当的外接圆与相切，切点为M时， 最大，
设外接圆的圆心为E，Q是异于点M的一点，连接，，交圆于点T，
则，根据三角形外角性质，得，故，
∴最大，
设与圆交于点H，连接，，根据切线性质，
∴，
作直径，连接，
∴，，
∵，
∴，
∴，
∴，
∴，
∴，
∴，
设，则，
∴，
∴，
过点E作，垂足为F，过点C作，垂足为G，交于点P，
根据垂径定理，得，四边形是矩形，
∴，

根据，得，
∴，
∴，
在直角三角形中，
∴，
∴，
∴，
∴，
解得，（舍去），
∴，
故，∴当最大时，．
训练题03【2023·湖南怀化·中考真题】
【答案】(1)
(2)见解析
【分析】（1）待定系数法求解析式即可求解；
（2）设、，的中点坐标为，联立，消去，整理得：，得出，则，设点到的距离为，则，依题意，，，得出，则，，点总在上，为直径，且与相切，即可得证．
【详解】（1）解：将代入，得
，解得：，∴抛物线解析式为：；
（2）解：设、，的中点坐标为，
联立，消去，整理得：，
∴，
∴，
∴，
∴，
设点到的距离为，则，
∵、，
∴，
∴
∴，
∴

∴，
∴点总在上，为直径，且与相切，
∴为直角．
∴无论为何值，平行于轴的直线上总存在一点，使得为直角．
训练题04【2023·江苏无锡·统考三模】
【答案】(1)
(2)
(3)存在，或
【分析】（1）把点A的坐标代入函数解析式中，求出b即可；
（2）求出点B的坐标，求出直线的解析式，过点C、D作x轴的垂线，垂足分别为E、F；设点C的坐标后，则由相似三角形的性质，可表示出点D的坐标，由点D在抛物线上，则可求得点D的坐标；
（3）存在；由定边定角知，作的外接圆，连接，过M作轴于N，则可得是等腰直角三角形，垂直平分，从而可求得M的坐标及圆的半径；设点P的坐标，由建立方程，即可求得点P的坐标．
【详解】（1）解：把点A的坐标代入函数解析式中，，
解得：，
故所求的解析式为；
（2）解：∵点B在抛物线，
∴，
即；
设直线解析式为为，
则有，
解得：，
∴直线解析式为为；
过点C、D作x轴的垂线，垂足分别为E、F，如图，
设，则；
∵，
∴，
∴，
则，
∴；
∵点D在抛物线上，
∴，
解得：，
则点D的坐标为；
（3）解：存在；
如图，作的外接圆，连接，过M作轴于N，
∴，
∴是等腰直角三角形，垂直平分，
∴，
∴M的坐标为，的半径；
设点P的坐标为，
则，
即，
由于，
∴方程整理得：，
解得：，
点P的坐标为或．
训练题05【2022·湖南长沙·长郡九年级期中】
【解答】解：（1）令y＝0，则﹣2x＝0，解得：x＝0或8．∴A（8，0）．
∴OA＝8．∵y＝﹣2x＝﹣4，∴B（4，﹣4）．过点B作BD⊥OA于点D，如图，
则OD＝4，BD＝4，∴OD＝BD，∴∠AOB＝∠OBD＝45°；
（2）①设⊙A与x轴交于点C，则C（4，0）．连接BC，如图，
∵B（4，﹣4），∴BC⊥OA．∵CO＝CB＝4，∴△CBO是以OB为底的等腰三角形．
∴点M与点C重合时，△MBO是以OB为底的等腰三角形．此时点M（4，0）；
过点A作AM⊥x轴，交⊙A于点M，延长MA交⊙A于点E，连接BE，
过点M作MF⊥y轴于点F，如图，
则M（8，4），E（8，﹣4），F（0，4）．∴MF＝ME＝8．∵B（4，﹣4），∴BE∥x轴．
∴BE⊥ME，BE＝4．∴∠BEM＝∠MFO＝90°，BE＝OF＝4．
在△MOF和△MBE中，，∴△MOF≌△MBE（SAS）．
∴MO＝MB．∴△MBO是以OB为底的等腰三角形．此时点M（8，4）；
综上，当△OBM是以OB为底的等腰三角形时，点M的坐标为（4，0）或（8，4）；
②设⊙A与x轴交于点C，则C（4，0）．连接BC，CN，AM，如图，
∵A（8，0），∴点C是OA的中点．∵N为OM的中点，∴CN是△OMA的中位线．∴CN＝AM＝2．
当点M在⊙A上运动时，由三角形的三边的关系定理可知：BC﹣CN≤BN≤BC+CN．
∵BC＝4，∴4﹣2≤BN≤4+2．∴线段BN长度的取值范围为：2≤BN≤6．
训练题06【2022·浙江嘉兴·统考二模】
【分析】（1）先求出二次函数y＝x2﹣4x+3图象与x轴、y轴的交点，再计算这三个交点是否在以P（2，2）为圆心，为半径的圆上，即可作出判断．
（2）由题意可得，二次函数y＝x2﹣4x+4图象的顶点A（2，0），与y轴的交点H（0，4），所以△POA周长＝PO+PA+OA＝PO+PH+2≥OH+2，即可得出最小值．
（3）连接CD，PA，设二次函数y＝ax2﹣4x+4图象的对称轴l与CD交于点E，与x轴交于点F，由对称性知，对称轴l经过点P，且l⊥CD，设PE＝m，由∠CPD＝120°，可得PA＝PC＝2m，CE＝m，PF＝4﹣m，因为二次函数y＝ax2﹣4x+4图象的对称轴l为，AB＝，所以AF＝BF＝，，在Rt△PAF中，利用勾股定理建立方程，求得m的值，进而得出a的值．
【解答】解：（1）对于二次函数y＝x2﹣4x+3，
当x＝0时，y＝3；当y＝0时，解得x＝1或x＝3，
∴二次函数图象与x轴交点为A（1，0），B（3，0），与y轴交点为C（0，3），
∵点P（2，2），
∴PA＝PB＝PC＝，
∴⊙P是二次函数y＝x2﹣4x+3的坐标圆．
（2）如图1，连接PH，
∵二次函数y＝x2﹣4x+4图象的顶点为A，坐标圆的圆心为P，
∴A（2，0），与y轴的交点H（0，4），
∴△POA周长＝PO+PA+OA＝PO+PH+2≥OH+2＝6，
∴△POA周长的最小值为6．
（3）如图2，连接CD，PA，
设二次函数y＝ax2﹣4x+4图象的对称轴l与CD交于点E，与x轴交于点F，
由对称性知，对称轴l经过点P，且l⊥CD，
∵AB＝，
∴AF＝BF＝，
∵∠CPD＝120°，PC＝PD，C（0，4），
∴∠PCD＝∠PDC＝30°，
设PE＝m，则PA＝PC＝2m，CE＝m，PF＝4﹣m，
∵二次函数y＝ax2﹣4x+4图象的对称轴l为，
∴，即，
在Rt△PAF中，PA2＝PF2+AF2，
∴，
即，
化简，得，解得，
∴．

训练题07【2023·江苏苏州·统考一模】
【答案】(1)A-2，0，B2m，0，C0，m
(2)m=4，P3，52
(3)P点坐标为3，0或3，52
【分析】（1）将x=0，y=0，分别代入y=-14x2+12m-1x+m，计算求解即可；
（2）如图1，连接PB，由题意知，PA=PB，则PA+PC=PB+PC，可知当C，P，B三点共线时，PA+PC值最小，在Rt△BOC中，由勾股定理得BC=5m，由PA+PC的最小值等于45，可得5m=45，计算m的值，然后得出B，C的点坐标，待定系数法求直线BC的解析式，根据P是直线BC与直线l的交点，计算求解即可；
（3）由（2）知m=4，则B8，0，C0，4，抛物线的对称轴为直线x=3，勾股定理逆定理判断△ABC是直角三角形，且∠ACB=90°，记D为直线l与x轴的交点，如图2，连接CD，由直角三角形斜边的中线等于斜边的一半可得CD=BD=AD，由等边对等角可得∠DCB=∠ABC，由三角形外角的性质可得∠ADC=∠DCB+∠ABC=2∠ABC，进而可得∠ADC=∠APC，即P与D重合，求此时的P点坐标；过A，C，D三点作⊙O'，如图2，由同弧所对的圆周角相等可知⊙O'与直线l=3交点即为P，设P3，a，由题意知，圆心O'在直线x=12上，设圆心坐标为12，n， 则AO'2=CO'2=PO'2，根据AO'2=CO'2，可求n值，根据AO'2=PO'2，可求a值，进而可得此时的P点坐标．
【详解】（1）解：当x=0时，y=m，
当y=0时，-14x2+12m-1x+m=0，整理得x2-2m-1x-4m=0，即x-2mx+2=0，
解得x1=2m，x2=-2，
∴A-2，0，B2m，0，C0，m，
（2）解：如图1，连接PB，
由题意知，PA=PB，
∴PA+PC=PB+PC，
∴当C，P，B三点共线时，PA+PC值最小，
在Rt△BOC中，由勾股定理得BC=OB2+OC2=4m2+m2=5m，
∵PA+PC的最小值等于45，
∴5m=45，
解得m=4，
∴B8，0，C0，4，
∴抛物线的对称轴为直线x=3，
设直线BC的解析式为y=kx+b，
将B8，0，C0，4代入得，0=8k+b4=b，
解得k=-12b=4，
∴直线BC的解析式为y=-12x+4，
当x=3时，y=-12×3+4=52，
∴P3，52，
∴m=4，P3，52；
（3）解：∵m=4，
∴B8，0，C0，4，抛物线的对称轴为直线x=3，
∵AC2=22+42=20，BC2=452=80，AB2=102=100，
∴AC2+BC2=AB2，
∴△ABC是直角三角形，且∠ACB=90°，
记D为直线l与x轴的交点，如图2，连接CD，
∴CD=BD=AD，
∴∠DCB=∠ABC，
∵∠ADC=∠DCB+∠ABC=2∠ABC，
∴∠ADC=∠APC，
∴P与D重合，即P3，0；
过A，C，D三点作⊙O'，如图2，由同弧所对的圆周角相等可知⊙O'与直线l=3交点即为P，设P3，a，
由题意知，圆心O'在直线x=12上，设圆心坐标为12，n， 则AO'2=CO'2=PO'2，
∵AO'2=CO'2，即-2-122+0-n2=0-122+4-n2，
解得n=54，
∵AO'2=PO'2，即-2-122+0-542=3-122+a-542，
解得a1=0，a2=52，
∴P3，52，
综上，P点坐标为3，0或3，52．
训练题08【2021·甘肃兰州·中考真题】
【答案】（1）（2）或
【分析】（1）直接将A、B两点的坐标代入列方程组解出即可；
（2）当时，，此时点在二次函数的对称轴上，以点为圆心，长为半径作圆，交于两点，得出，再根据（同弧所对圆周角），即可解答
【详解】（1）将点代入，得：
，解得：所以，二次函数的表达方式为：
（2）当时，，此时点在二次函数的对称轴上，
以点为圆心，长为半径作圆，交于两点
点在该圆上
（同弧所对圆周角）
或
训练题09【2022•福建·统考模拟】
【分析】（1）等腰直角三角形斜边中线等于斜边一半，点的坐标，不难求出A、B两点坐标，把点A、B、C代入二次函数解析式，解三元一次方程组就可得到函数解析式．
（2））通过设过点D（2，0）的直线MN解析式为y＝k（x﹣2）＝kx﹣2k，得到关于x、关于y的方程，利用跟与系数的关系，再得到圆的解析式，待定系数法确定定点的x、y的值，确定定点的坐标．
【解答】解：连接AC、BC，过点C作CP垂直于x轴于点P．
在Rt△CAB中，AC＝BC，CP⊥AB，点C（2，﹣4），
∴CP＝AP＝PB＝4，OP＝2，
∴OA＝AP﹣OP＝4﹣2＝2，OB＝OP+PB＝4+2＝6，
∴点A（﹣2，0），点B（6，0），
把点A（﹣2，0），点B（6，0），点C（2，﹣4）代入函数解析式得
，
解得，
∴抛物线的解析式为：y＝x2﹣x﹣3．
故答案为：y＝x2﹣x﹣3．
（2）设过点D（2，0）的直线MN解析式为y＝k（x﹣2）＝kx﹣2k，
联立直线与抛物线解析式得关于x的等式：kx﹣2k＝x2﹣x﹣3，
化简得＝0，
xN+xM＝﹣＝4（k+1），xNxM＝＝8k﹣①，
联立直线与抛物线解析式得关于y的等式：y＝（+2）2﹣（+2）﹣3，
化简得y2+（﹣﹣1）y﹣4＝0，
yM+yN＝4k2，yMyN＝﹣②，
线段MN的中点就是圆的圆心，
∴xO＝（xN+xM）＝2（K+1），
代入直线方程得yO＝2k2，
∴圆心坐标为（2k+2，2k2），
直径MN＝＝，
把①、②代入上式化简整理得直径MN＝，
设圆上某一点（x，y）到圆心的距离等于半径，
∴＝，
化简整理得16k2+12﹣8k＝x2﹣4kx﹣4x+y2﹣4k2y＝﹣4yk2﹣4kx+x2﹣4x+y2，
圆过定点，所以与k值无关，看作是关于k的二次等式，
k2、k的系数，常量对应相等，
得﹣8＝﹣4x，
x＝2，
16＝﹣4y，
y＝﹣4，
由以上分析，所以以MN为直径的圆过定点（2，﹣4）．
故答案为：以线段MN为直径的圆过定点（2，﹣4）．
训练题10【2022·上海闵行·二模】
【分析】（1）根据点A、B的坐标，设抛物线y＝a（x+1）（x﹣3），再将点C代入即可求出a的值，从而得出答案；
（2）①分两种情形，当r⊙G＞r⊙E时，则GB﹣EF＝GE，则EF＝EB，当r⊙G＜r⊙E时，则EF﹣GB＝GE，设EF＝5t，FG＝3t，GE＝4t，则5t﹣GB＝4t，则GB＝t＜GE＝4t，从而得出矛盾；
②由．设BD＝t，则DE＝，利用勾股定理得BE＝，则F坐标为（3﹣t，3t），代入抛物线解析式，从而解决问题．
【解答】解：（1）∵点A坐标为（﹣1，0），点B坐标为（3，0）．
设抛物线y＝a（x+1）（x﹣3）（a≠0），
∵抛物线经过点C（0，4），
∴4＝﹣3a．
解得．
∴抛物线的表达式是；
（2）①由于⊙G与⊙E内切，
当r⊙G＜r⊙E时，则EF﹣GB＝GE，
设EF＝5t，FG＝3t，GE＝4t，则5t﹣GB＝4t，
∴GB＝t＜GE＝4t，
∴点E在线段CB的延长线上．
又∵已知点E在线段BC上，
∴矛盾，因此不存在．
当r⊙G＞r⊙E时，则GB﹣EF＝GE，
又∵GE＝GB﹣EB，
∴EF＝EB；
②∵OC⊥OB，FD⊥OB，
∴∠COB＝∠EDB＝90°．
∴．
∴设BD＝t，则DE＝；
在Rt△BED中，由勾股定理得，
．
∴，
∴F坐标为（3﹣t，3t），
∵F点在抛物线上，
∴，
∴解得，t＝0（点F与点B重合，舍去）．
∴F坐标为（，）．