资料中包含下列文件，点击文件名可预览资料内容
还剩3页未读，
继续阅读
广东省广州市越秀区广东实验中学2023-2024学年九年级下学期开学考试数学试题（原卷版+解析版）
展开
这是一份广东省广州市越秀区广东实验中学2023-2024学年九年级下学期开学考试数学试题（原卷版+解析版），文件包含精品解析广东省广州市越秀区广东实验中学2023-2024学年九年级下学期开学考试数学试题原卷版docx、精品解析广东省广州市越秀区广东实验中学2023-2024学年九年级下学期开学考试数学试题解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
1. 下列疫情防控宣传图片中，是轴对称图形的是（ ）
A. B.
C. D.
2. 抛物线向左平移1个单位，再向下平移1个单位后的抛物线解析式是（ ）
A. B.
C. D.
3. 用配方法解方程x2＋1=8x，变形后的结果正确的是( )
A. (x＋4)2=15B. (x＋4)2=17C. (x－4)2=15D. (x－4)2=17
4. 已知半径为4，圆心在坐标原点上，点的坐标为，则点与的位置关系是（ ）
A. 点在内B. 点在上C. 点在外D. 不能确定
5. 一个不透明的盒子中有100个红色小球，10个白色小球，1个黄色小球，现从中随机取出一个球，下列事件是不可能事件的是（ ）
A. 取出的是红色小球B. 取出的是白色小球
C. 取出的是黄色小球D. 取出的是黑色小球
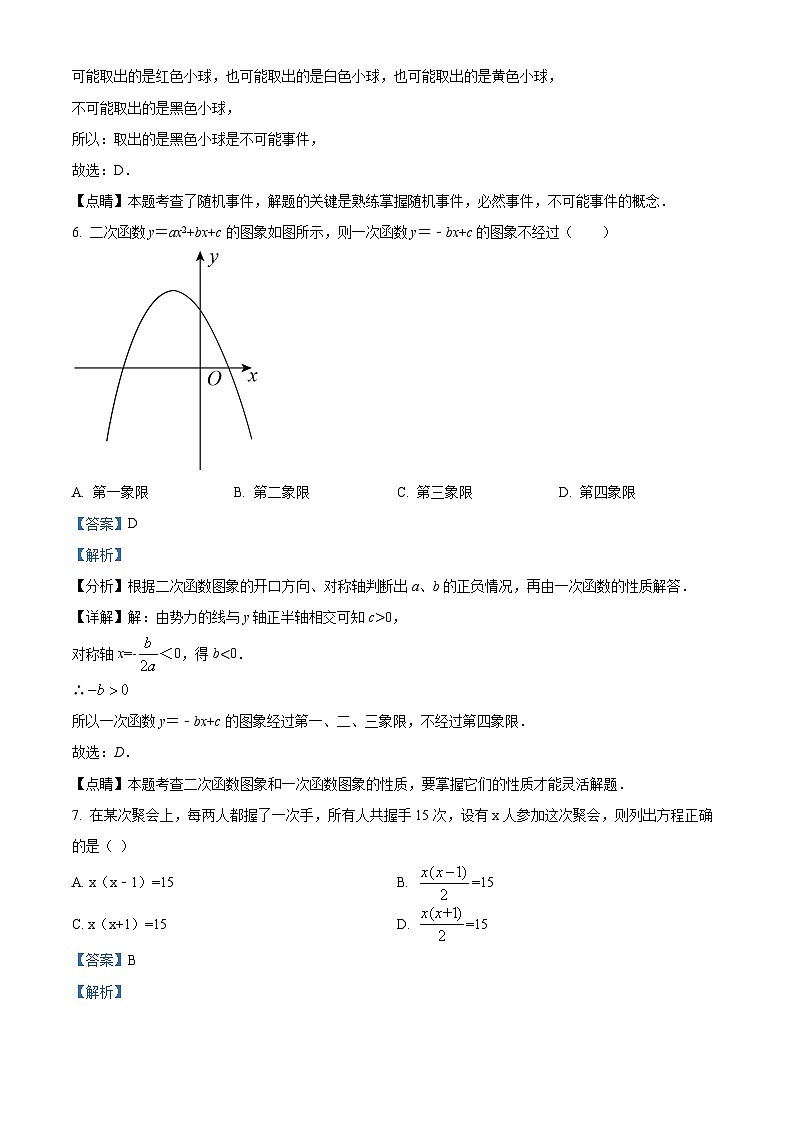
6. 二次函数y＝ax2+bx+c图象如图所示，则一次函数y＝﹣bx+c的图象不经过（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
7. 在某次聚会上，每两人都握了一次手，所有人共握手15次，设有x人参加这次聚会，则列出方程正确的是（ ）
A. x（x﹣1）=15B. =15
C. x（x+1）=15D. =15
8. 如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE∽△DEF，AB=6，AE=9，DE=2，则EF的长是（ ）
A. 4B. 5C. D.
9. 如图，将△ABC绕点C顺时针旋转α得到△DEC，此时点D落在边AB上，且DE垂直平分BC，则的值是（ ）
A. B. C. D.
10. 已知抛物线y＝ax2+bx+c（a，b，c为常数且a≠0）经过P1（1，y1），P2（2，y2），P3（3，y3），P4（4，y4）四点．若y1＜y2＜y3，则下列说法中正确的是（ ）
A. 若y4＞y3，则a＞0
B. 对称轴不可能是直线x＝2.7
C. y1＜y4
D 3a+b＜0
二、填空题（本大题共6小题，共18.0分）
11. 在平面直角坐标系中，点P（﹣10，a）与点Q（b，1）关于原点对称，则a+b＝_____．
12. 圆锥的底面半径为，母线长是，则圆锥的侧面积是______（结果保留）．
13. 如图，小明为了测量树的高度CD，他在与树根同一水平面上的B处放置一块平面镜，然后他站在A处刚好能从镜中看到树顶D，已知A、B、C三点在同一直线上，且AB＝2m，BC＝8m．他的眼睛离地面的高度1.6m，则树的高度CD为__m．
14. 如图，在▱ABCD中，∠A=65°，将▱ABCD绕顶点B顺时针旋转到▱，当首次经过顶点C时，旋转角∠的大小为_______．
15. 飞机着陆后滑行的距离（米）关于滑行的时间（秒）的函数解析式是：．则飞机着陆后滑行到停下来滑行的距离为_______米．
16. 如图所示，ABCD是边长为2的正方形，点E，F分别为边BC，CD上动点（点E不与B，C重合，点F不与C，D重合），且∠EAF＝45°，下列说法：
①点E从B向C运动的过程中，△CEF的周长始终不变；
②以A为圆心，2为半径的圆一定与EF相切；
③△AEF面积有最小值；
④△CEF的面积最大值小于．
其中正确的有 _____.（填写序号）
三、解答题（本大题共9小题，共72分）
17. 解一元二次方程：．
18. 如图，△ABC中，CD是边AB上的高，且．
（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．
19. 如图，在平面直角坐标系中，△ABC的顶点均在格点上，A（1，0）、B（2，﹣2），C（4，﹣1）．将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1．
（1）画出△A1B1C1；
（2）求点C在旋转过程中运动路径长．（结果保留π）
20. 有A、B两组卡片，卡片上除数字外完全相同，A组有三张，分别标有数字1、2、；B组有二张，分别标有数字、2．小明闭眼从A组中随机抽出一张，记录其标有的数字为x，再从B组中随机抽出一张，记录其标有的数字为y，这样就确定点P的一个坐标为．
（1）用列表或画树状图的方法写出点P的所有可能坐标；
（2）求点P落在第一象限的概率．
21. 如图，抛物线y＝x2+bx+c与x轴交于A（﹣3，0）、B两点，与y轴交于点C（0，﹣3）．
（1）求抛物线的解析式；
（2）结合图形，求y＞0时自变量x的取值范围．
22. 如图，在中，是直径，点是圆上一点，在的延长线上取一点，连接，使．求：
（1）求证：直线是的切线；
（2）若，求扇形面积
23. 某快餐店试销某种套餐，每份套餐的成本为5元，该店每天固定支出费用为600元（不含套餐成本）．试销一段时间后发现，若每份套餐售价不超过10元，每天可销售400份；若每份套餐售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x（元）取整数，用y（元）表示该店每天的利润．
（1）若每份套餐售价不超过10元．
①试写出y与x的函数关系式；
②若要使该店每天的利润不少于800元，则每份套餐的售价应为多少元？
（2）该店把每份套餐的售价提高到10元以上，每天的利润能否达到1560元？若不能，请说明理由；若能，求出每份套餐的售价应定为多少元时，既能保证利润又能吸引顾客？
24. 如图，在⊙O中，AB为弦，CD为直径，且AB⊥CD，垂足为E，P为上动点（不与端点重合），连接PD．
（1）求证：∠APD＝∠BPD；
（2）利用尺规在PD上找到点I，使得I到AB、AP的距离相等，连接AD（保留作图痕迹，不写作法）．求证：∠AIP+∠DAI＝180°；
（3）在（2）的条件下，连接IC、IE，若∠APB＝60°，试问：在P点的移动过程中，是否为定值？若是，请求出这个值；若不是，请说明理由．
25. 已知抛物线G：y1＝mx2﹣（3m﹣3）x+2m﹣3，直线h：y2＝mx+3﹣2m，其中m≠0．
（1）当m＝1时，求抛物线G与直线h交点的坐标；
（2）求证：抛物线G与直线h必有一个交点A在坐标轴上；
（3）在（2）的结论下，解决下列问题：
①无论m怎样变化，求抛物线G一定经过的点坐标；
②将抛物线G关于原点对称得到的图象记为抛物线，试结合图象探究：若在抛物线G与直线h，抛物线与直线h均相交，在所有交点的横坐标中，点A横坐标既不是最大值，也不是最小值，求此时抛物线G的对称轴的取值范围．
1. 下列疫情防控宣传图片中，是轴对称图形的是（ ）
A. B.
C. D.
2. 抛物线向左平移1个单位，再向下平移1个单位后的抛物线解析式是（ ）
A. B.
C. D.
3. 用配方法解方程x2＋1=8x，变形后的结果正确的是( )
A. (x＋4)2=15B. (x＋4)2=17C. (x－4)2=15D. (x－4)2=17
4. 已知半径为4，圆心在坐标原点上，点的坐标为，则点与的位置关系是（ ）
A. 点在内B. 点在上C. 点在外D. 不能确定
5. 一个不透明的盒子中有100个红色小球，10个白色小球，1个黄色小球，现从中随机取出一个球，下列事件是不可能事件的是（ ）
A. 取出的是红色小球B. 取出的是白色小球
C. 取出的是黄色小球D. 取出的是黑色小球
6. 二次函数y＝ax2+bx+c图象如图所示，则一次函数y＝﹣bx+c的图象不经过（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
7. 在某次聚会上，每两人都握了一次手，所有人共握手15次，设有x人参加这次聚会，则列出方程正确的是（ ）
A. x（x﹣1）=15B. =15
C. x（x+1）=15D. =15
8. 如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE∽△DEF，AB=6，AE=9，DE=2，则EF的长是（ ）
A. 4B. 5C. D.
9. 如图，将△ABC绕点C顺时针旋转α得到△DEC，此时点D落在边AB上，且DE垂直平分BC，则的值是（ ）
A. B. C. D.
10. 已知抛物线y＝ax2+bx+c（a，b，c为常数且a≠0）经过P1（1，y1），P2（2，y2），P3（3，y3），P4（4，y4）四点．若y1＜y2＜y3，则下列说法中正确的是（ ）
A. 若y4＞y3，则a＞0
B. 对称轴不可能是直线x＝2.7
C. y1＜y4
D 3a+b＜0
二、填空题（本大题共6小题，共18.0分）
11. 在平面直角坐标系中，点P（﹣10，a）与点Q（b，1）关于原点对称，则a+b＝_____．
12. 圆锥的底面半径为，母线长是，则圆锥的侧面积是______（结果保留）．
13. 如图，小明为了测量树的高度CD，他在与树根同一水平面上的B处放置一块平面镜，然后他站在A处刚好能从镜中看到树顶D，已知A、B、C三点在同一直线上，且AB＝2m，BC＝8m．他的眼睛离地面的高度1.6m，则树的高度CD为__m．
14. 如图，在▱ABCD中，∠A=65°，将▱ABCD绕顶点B顺时针旋转到▱，当首次经过顶点C时，旋转角∠的大小为_______．
15. 飞机着陆后滑行的距离（米）关于滑行的时间（秒）的函数解析式是：．则飞机着陆后滑行到停下来滑行的距离为_______米．
16. 如图所示，ABCD是边长为2的正方形，点E，F分别为边BC，CD上动点（点E不与B，C重合，点F不与C，D重合），且∠EAF＝45°，下列说法：
①点E从B向C运动的过程中，△CEF的周长始终不变；
②以A为圆心，2为半径的圆一定与EF相切；
③△AEF面积有最小值；
④△CEF的面积最大值小于．
其中正确的有 _____.（填写序号）
三、解答题（本大题共9小题，共72分）
17. 解一元二次方程：．
18. 如图，△ABC中，CD是边AB上的高，且．
（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．
19. 如图，在平面直角坐标系中，△ABC的顶点均在格点上，A（1，0）、B（2，﹣2），C（4，﹣1）．将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1．
（1）画出△A1B1C1；
（2）求点C在旋转过程中运动路径长．（结果保留π）
20. 有A、B两组卡片，卡片上除数字外完全相同，A组有三张，分别标有数字1、2、；B组有二张，分别标有数字、2．小明闭眼从A组中随机抽出一张，记录其标有的数字为x，再从B组中随机抽出一张，记录其标有的数字为y，这样就确定点P的一个坐标为．
（1）用列表或画树状图的方法写出点P的所有可能坐标；
（2）求点P落在第一象限的概率．
21. 如图，抛物线y＝x2+bx+c与x轴交于A（﹣3，0）、B两点，与y轴交于点C（0，﹣3）．
（1）求抛物线的解析式；
（2）结合图形，求y＞0时自变量x的取值范围．
22. 如图，在中，是直径，点是圆上一点，在的延长线上取一点，连接，使．求：
（1）求证：直线是的切线；
（2）若，求扇形面积
23. 某快餐店试销某种套餐，每份套餐的成本为5元，该店每天固定支出费用为600元（不含套餐成本）．试销一段时间后发现，若每份套餐售价不超过10元，每天可销售400份；若每份套餐售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x（元）取整数，用y（元）表示该店每天的利润．
（1）若每份套餐售价不超过10元．
①试写出y与x的函数关系式；
②若要使该店每天的利润不少于800元，则每份套餐的售价应为多少元？
（2）该店把每份套餐的售价提高到10元以上，每天的利润能否达到1560元？若不能，请说明理由；若能，求出每份套餐的售价应定为多少元时，既能保证利润又能吸引顾客？
24. 如图，在⊙O中，AB为弦，CD为直径，且AB⊥CD，垂足为E，P为上动点（不与端点重合），连接PD．
（1）求证：∠APD＝∠BPD；
（2）利用尺规在PD上找到点I，使得I到AB、AP的距离相等，连接AD（保留作图痕迹，不写作法）．求证：∠AIP+∠DAI＝180°；
（3）在（2）的条件下，连接IC、IE，若∠APB＝60°，试问：在P点的移动过程中，是否为定值？若是，请求出这个值；若不是，请说明理由．
25. 已知抛物线G：y1＝mx2﹣（3m﹣3）x+2m﹣3，直线h：y2＝mx+3﹣2m，其中m≠0．
（1）当m＝1时，求抛物线G与直线h交点的坐标；
（2）求证：抛物线G与直线h必有一个交点A在坐标轴上；
（3）在（2）的结论下，解决下列问题：
①无论m怎样变化，求抛物线G一定经过的点坐标；
②将抛物线G关于原点对称得到的图象记为抛物线，试结合图象探究：若在抛物线G与直线h，抛物线与直线h均相交，在所有交点的横坐标中，点A横坐标既不是最大值，也不是最小值，求此时抛物线G的对称轴的取值范围．
相关试卷
广东省深圳市南外集团华侨城中学2023-2024学年九年级下学期开学开学数学试题（原卷版+解析版）： 这是一份广东省深圳市南外集团华侨城中学2023-2024学年九年级下学期开学开学数学试题（原卷版+解析版），文件包含精品解析广东省深圳市南外集团华侨城中学2023-2024学年九年级下学期开学开学数学试题原卷版docx、精品解析广东省深圳市南外集团华侨城中学2023-2024学年九年级下学期开学开学数学试题解析版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
33，广东省广州市越秀区广东实验中学2023-2024学年七年级上学期开学考试数学试题： 这是一份33，广东省广州市越秀区广东实验中学2023-2024学年七年级上学期开学考试数学试题，共12页。试卷主要包含了填空题，选择题，判断题，计算题，应用题等内容，欢迎下载使用。
广东省广州市越秀区2021-2022学年九年级上学期期末数学试题（原卷版）： 这是一份广东省广州市越秀区2021-2022学年九年级上学期期末数学试题（原卷版），文件包含单元质量评价六第6章试卷教师版2023-2024沪教版化学九年级下册docx、单元质量评价六第6章试卷学生版2023-2024沪教版化学九年级下册docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。
