

2024年辽宁省沈阳市中考一模考前数学练兵卷(三)(含答案)
展开1.一次社会调查中,某小组了解到某种品牌的薯片包装上注明净含量为60±5g,则下列同类产品中净含量不符合标准的是( )
A.56gB.60gC.64gD.68g
2.如图所示的几何体是由4个完全相同的小正方体组成,它的左视图是( )
A.B.C.D.
3.剪纸是我国具有独特艺术风格的民间艺术,反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中,是中心对称图形的有( )
A.①②③B.①②④C.①③④D.②③④
4.不等式组x−1<−32x+9<3的解集是( )
A.﹣3<x<3B.x>﹣2C.﹣3<x<﹣2D.x<﹣3
5.下列计算正确的是( )
A.m+m=2m2B.2m2•3m2=6m2
C.m6÷m3=m2D.(2m)3=8m3
6.如图,四边形ADBC内接于⊙O,四边形ADBO是平行四边形,则∠ABD的度数是( )
A.45°B.50°C.20°D.30°
7.某数学兴趣小组根据所学函数的经验,发现:当做功一定时,功率P(单位:W)与做功的时间t(单位:s)存在反比例函数关系.如表是他们实验的几组数据:
则功率P(W)与做功的时间t(s)之间的函数关系式是( )
A.P=1200tB.P=1200tC.P=t1200D.P=120t
8.如图,一次函数y=kx﹣2k(k<0)的图象经过点P(1,1),当0<kx﹣2k≤x时,x的取值范围是( )
A.x<1B.x>1C.0<x≤1D.1≤x<2
6题 8题 9题 10题
9.如图所示,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )
A.455B.235C.255D.433
10.如图,在Rt△ABC中,∠C=90°,以A为圆心,适当长为半径画弧,分别交AB,AC于D,E,再分别以D,E为圆心,大于12DE长为半径画弧,两弧在∠BAC的内部交于点F,作射线AF交BC于点M,若CM=3,AB=10,则△ABM的面积为( )
A.30B.15C.10D.3
二.填空题(共5小题,每小题3分,共15分)
11.分解因式2a2b﹣8b3= .
12.用科学记数法表示25040000,应记作 .
13.《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云阔不及长一十二步,问长及阔各几步”.意思是:一块矩形田地的面积为864平方步,只知道它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为 .
14.如图,矩形OABC的顶点A、C分别在x轴、y轴上,B(﹣2,1),将△OAB绕点O顺时针旋转,点B落在y轴上的点D处,得到△OED,OE交BC于点G,若反比例函数y=kx(x<0)的图象经过点G,则k的值为 .
15.如图,将一个长方形纸片沿着直线MN对折后,顶点C恰好落在边AB上的点E处,点D落在F处,且∠AEF=30°,若CN=5,CD=4,则AE的长为 .
14题 15题
三.解答题(共8小题,共75分)
16.(每小题5分,共10分)
(1)计算3×6−12+(2)2;(2)解方程组:2x−5y=−114x+3y=17.
17.(8分)习总书记在党的第二十次全国代表大会上,报告指出:“积极稳妥推进碳达峰碳中和”.某公司积极响应节能减排号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车进价是每辆B型汽车进价的1.5倍,若用1500万元购进A型汽车的数量比1200万元购进B型汽车的数量少20辆.求每辆B型汽车进价是多少万元?
18.(9分)为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
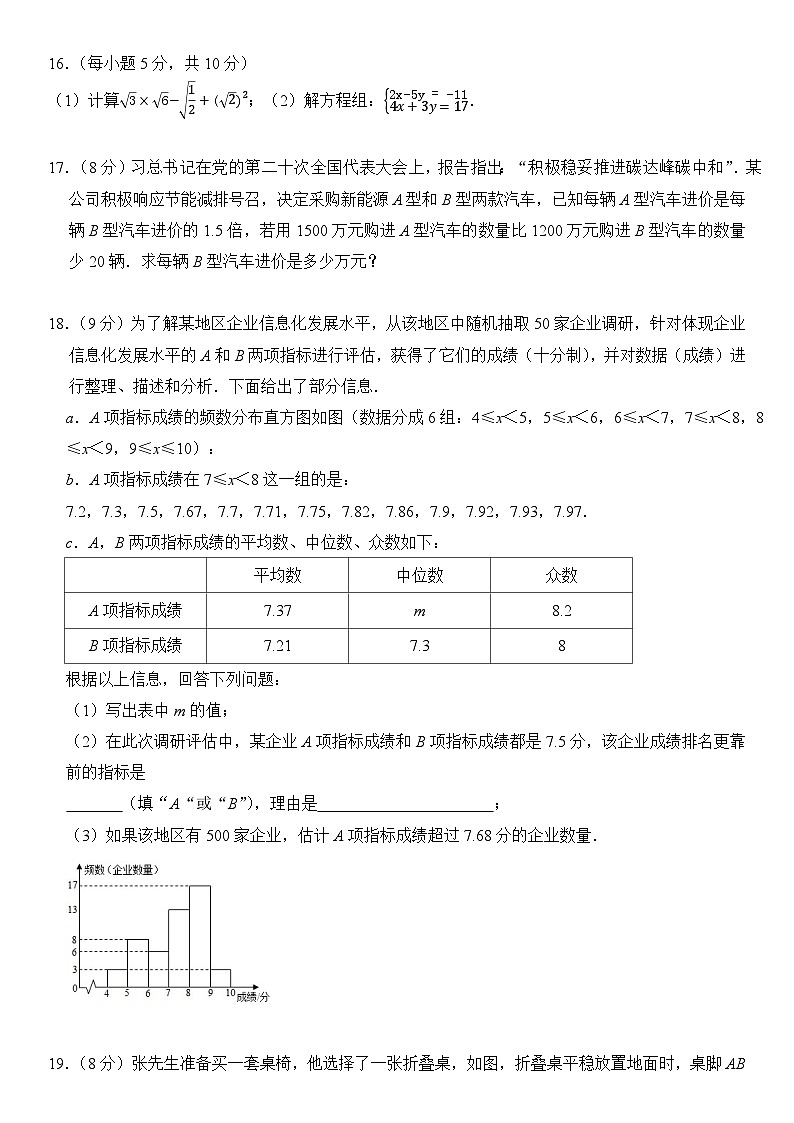
a.A项指标成绩的频数分布直方图如图(数据分成6组:4≤x<5,5≤x<6,6≤x<7,7≤x<8,8≤x<9,9≤x≤10):
b.A项指标成绩在7≤x<8这一组的是:
7.2,7.3,7.5,7.67,7.7,7.71,7.75,7.82,7.86,7.9,7.92,7.93,7.97.
c.A,B两项指标成绩的平均数、中位数、众数如下:
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是
(填“A“或“B”),理由是 ;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.
19.(8分)张先生准备买一套桌椅,他选择了一张折叠桌,如图,折叠桌平稳放置地面时,桌脚AB与CD相交于点O,AO=OC,OB=OD,AO:OB=1:2,AB=84cm,∠AOC=56°.
(1)求点O至AC的距离;
(2)张先生想为这张折叠桌配把椅子,《中华人民共和国国家标准》中指出,桌椅高度差应控制在28cm至32cm范围内(包括28cm与32cm),现有两种规格的椅子可供挑选,甲种椅子高度为40cm,乙种椅子高度为44cm,请问张先生挑选哪种椅子比较合适,为什么?(参考数据:sin28°≈0.47,cs28°≈0.88,tan28°≈0.53)
20.(8分)某商场购进一种每件成本为80元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系.
(1)求出y与x之间的函数关系式;
(2)疫情期间,有关部门规定每件商品的利润率不得超过25%,那么将售价定为多少,来保证每天获得的总利润最大,最大总利润是多少?
21.(8分)如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
(1)求证:FD是⊙O的切线;
(2)若AF=6,tan∠BDF=14,求EF的长.
22.(12分)[问题背景]
综合与实践课上,数学王老师分发给每位同学若干张相同的长方形纸片王老师取出三张纸片演示操作,依次将纸片沿事先画出的竖直和水平方向的实线裁剪成若干个完全相同的小长方形.
[分析问题]
(1)请补全上面表格,并在图1所示的平面直角坐标系中描出表中各对数值所对应的点(n,m),再用平滑曲线连接.根据绘制的图象猜想,裁剪得到的小长方形个数m与纸片序号n序号可能存在函数关系(填类型).[猜想验证]
为了验证这一猜想,爱研究的同学从“形”的角度出发,发现裁剪得到的小长方形个数可以用“行数×列数”的方法得到.
(2)请直接写出裁剪得到的小长方形个数m与纸片序号n之间的函数关系式为 .
[解决问题]
某农科研究所有一块矩形的耕地ABCD(如图2),AB=40m,BC=35m,现需要将其分成若干小长方形耕地,进行不同种子的育种实验.按照[问题背景]中的分割方式,爱思考的同学提出以下2个问题.
(3)若将此耕地分成56个完全相同的小长方形耕地,求竖直方向分割用的实线数量.
(4)为了方便科研人员观察并收集实验数据,将竖直和水平方向的实线换成1米宽的小路,若小路的面积之和占此耕地面积的36%,求小长方形耕地的总数量.
23.(12分)如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
参考答案
一.选择题(共10小题)
1.D.2.A.3.A.4.D.5.D.6.D.7.A.8.D.9.A.10.B.
二.填空题(共5小题)
11.2b(a+2b)(a﹣2b).12.2.504×107.13.x(x+12)=864.14.−12.15.32.
三.解答题(共8小题)
16.解:(1)3×6−12+(2)2
=3×6−12+2
=18−22+2
=32−22+2
=522+2;
(2)2x−5y=−11①4x+3y=17②,
②﹣①×2,得:13y=39,
解得y=3,
将y=3代入①,得:x=2,
∴该方程组的解为x=2y=3.
17.解:设每辆B型汽车进价是x万元,则每辆A型汽车进价是1.5x万元,
根据题意得:1200x−15001.5x=20,
解得:x=10,
经检验,x=10是所列方程的解,且符合题意.
答:每辆B型汽车进价是10万元.
18.解:(1)m=(7.82+7.86)÷2=7.84;
(2)该企业成绩排名更靠前的指标是B,
理由是:该企业A项指标成绩是7.5分,小于A项指标成绩的中位数,说明该企业指标成绩的排名在后25名;
B项指标成绩是7.5分,大于B项指标成绩的中位数,说明该企业B项指标成绩的排名在前25名;
故答案为:B,该企业A项指标成绩是7.5分,小于A项指标成绩的中位数,说明该企业指标成绩的排名在后25名;B项指标成绩是7.5分,大于B项指标成绩的中位数,说明该企业B项指标成绩的排名在前25名;
(3)根据题意可知:
在样本中,A项指标成绩超过7.68分的企业数量是29,
因为2950×500=290.
所以估计该地区A项指标成绩超过7.68分的企业数量为290家.
19.解:(1)如图,过点O作OH⊥AC于点H,
∵AO:OB=1:2,AB=84cm,
∴OA=28cm,OB=56cm,
∵OA=OC,∠AOC=56°.
∴∠AOH=∠COH=28°,
∴OH=OA×cs28°≈28×0.88=24.64(cm);
(2)延长HO与BD交于点G,
∵OB=OD=56cm,∠DOG=∠BOG,
∴OG⊥BD,
∴OG=OB×cs28°≈56×0.88=49.28(cm),
∴GH=OH+OG=24.64+49.28=73.92(cm),
甲种:73.92﹣40=33.92,不在28cm至32cm范围内;
乙种:73.92﹣44=29.92,在28cm至32cm范围内.
所以张先生挑选乙种椅子比较合适.
20.解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
由所给函数图象可知:100k+b=50120k+b=30,
解得:k=−1b=150.
∴y=﹣x+150,
令y=0,则﹣x+150=0,
解得:x=150.
故y与x的函数关系式为y=﹣x+150(80<x≤150).
(2)∵y=﹣x+150,
∴W=(x﹣8)y=(x﹣80)(﹣x+150)=﹣x2+230x﹣12000,
又由题意可得:x−8080≤25%,
解得:x≤100,
∴80<x≤100,
∵W=﹣x2+230x﹣12000=﹣(x﹣115)2+1225,
∴当x=100时,W有最大值,
且Wmax=﹣(100﹣115)2+1225=1000(元).
故将售价定为100元,每天获得的总利润最大,最大总利润是1000元.
21.(1)证明:连接OD,如图:
∵CO⊥AB,
∴∠COE=90°,
∴∠E+∠C=90°,
∵FE=FD,OD=OC,
∴∠E=∠FDE,∠C=∠ODC,
∴∠FDE+∠ODC=90°,
∴∠ODF=90°,
∴OD⊥DF,
∴FD是⊙O的切线;
(2)解:连接AD,如图:
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠A+∠ODB=90°,
∵∠BDF+∠ODB=90°,
∴∠A=∠BDF,
又∵∠DFB=∠AFD,
∴△FBD∽△FDA,
∴DFAF=BDAD,
∵tan∠A=tan∠BDF=BDAD=14,
∴DFAF=14,即DF6=14,
解得:DF=32,
∴EF=32.
22.解:(1)由图例知,当n=4时,如图:
共有20个小长方形;
当n=5时,如图:
共有30个小长方形;
故答案为:20,30;
描点,连线,
猜想:裁剪得到的小长方形个数m与纸片序号n序号可能存在函数关系为二次函数.
∴从“形”的角度出发,裁剪得到的小长方形个数可以用“行数×列数”的方法得到;
(2)小长方形个数m与纸片序号n之间的函数关系式为m=n(n+1),
验证:
由图例知,当n=1时,m=2=1×2,
当n=2时,m=6=2×3,
当n=3时,m=12=3×4,
当n=4时,m=20=4×5,
当n=5时,m=30=5×6,
...,
∴m=n(n+1),
故答案为:m=n(n+1);
(3)由题意得,n(n+1)=56,
∵n为正整数,
∴n=7,
∴竖直方向分割用的实线数量为7;
(4)设水平方向有n条道路,竖直方向有(n+1)条道路,
由题意得:40n+35(n+1)﹣n(n+1)=40×35×36%,
整理得:n2﹣74n+469=0,
解得:n=7或n=67(舍去),
∵n是水平方向小路数量,水平方向耕地数量为8,竖直方向耕地数量为9,
∴耕地块数为8×9=72(块),
∴小长方形耕地的总数量72块.
23.解:(1)BM+DN=MN,理由如下:
如图1,在MB的延长线上,截取BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=∠D=90°,
∴∠ABE=90°=∠D,
在△ABE和△ADN中,AB=AD∠ABE=∠DBE=DN,
∴△ABE≌△ADN(SAS),
∴AE=AN,∠EAB=∠NAD,
∴∠EAN=∠BAD=90°,
∵∠MAN=45°,
∴∠EAM=45°=∠NAM,
在△AEM和△ANM中,AE=AN∠EAM=∠NAMAM=AM,
∴△AEM≌△ANM(SAS),
∴ME=MN,
又∵ME=BE+BM=BM+DN,
∴BM+DN=MN;
故答案为:BM+DN=MN;
(2)(1)中的结论不成立,DN﹣BM=MN.理由如下:
如图2,在DC上截取DF=BM,连接AF,
则∠ABM=90°=∠D,
在△ABM和△ADF中,AB=AD∠ABM=∠DBM=DF,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∴∠BAM+∠BAF=∠BAF+∠DAF=∠BAD=90°,
即∠MAF=∠BAD=90°,
∵∠MAN=45°,
∴∠MAN=∠FAN=45°,
在△MAN和△FAN中,AM=AF∠MAN=∠FANAN=AN,
∴△MAN≌△FAN(SAS),
∴MN=NF,
∴MN=DN﹣DF=DN﹣BM,
∴DN﹣BM=MN.
(3)∵四边形ABCD是正方形,
∴AB=BC=AD=CD=6,AD∥BC,AB∥CD,∠ABC=∠ADC=∠BCD=90°,
∴∠ABM=∠MCN=90°,
∵CN=CD=6,
∴DN=12,
∴AN=AD2+DN2=62+122=65,
∵AB∥CD,
∴△ABQ∽△NDQ,
∴BQDQ=AQNQ=ABDN=612=12,
∴AQAN=13,
∴AQ=13AN=25;
由(2)得:DN﹣BM=MN.
设BM=x,则MN=12﹣x,CM=6+x,
在Rt△CMN中,由勾股定理得:62+(6+x)2=(12﹣x)2,
解得:x=2,
∴BM=2,
∴AM=AB2+BM2=62+22=210,
∵BC∥AD,
∴△PBM∽△PDA,
∴PMPA=BMDA=26=13,
∴PM=12AM=10,
∴AP=AM+PM=310.
t(单位:s)
10
20
30
40
50
P(单位:W)
120
60
40
30
24
平均数
中位数
众数
A项指标成绩
7.37
m
8.2
B项指标成绩
7.21
7.3
8
纸片序号n
1
2
3
4
5
裁剪得到的小长方形个数m
2
6
12
2022年辽宁省沈阳市中考数学考前模拟冲刺试题: 这是一份2022年辽宁省沈阳市中考数学考前模拟冲刺试题,共22页。
【历年真题】2022年辽宁省沈阳市中考数学考前摸底测评 卷(Ⅱ)(含详解): 这是一份【历年真题】2022年辽宁省沈阳市中考数学考前摸底测评 卷(Ⅱ)(含详解),共20页。试卷主要包含了下列命题,是真命题的是等内容,欢迎下载使用。
[中考专题]2022年辽宁省沈阳市中考数学三模试题(精选): 这是一份[中考专题]2022年辽宁省沈阳市中考数学三模试题(精选),共22页。试卷主要包含了有理数等内容,欢迎下载使用。












