46，广西壮族自治区南宁市第四十七中学2023-2024学年八年级上学期月考数学试卷（10月份）

这是一份46，广西壮族自治区南宁市第四十七中学2023-2024学年八年级上学期月考数学试卷（10月份），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）在1，﹣1.1，0，﹣3中，最小的数是（ ）
A．1B．﹣1.1C．0D．﹣3
2．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（ ）
A．B．C．D．
3．（3分）下列实数中，是无理数的为（ ）
A．B．3.14C．D．
4．（3分）如图，用不等式表示数轴上所示的解集，正确的是（ ）
A．x＜﹣1或x≥3B．x≤﹣1或x＞3C．﹣1≤x＜3D．﹣1＜x≤3
5．（3分）若点P（m，1）在第二象限内，则点Q（﹣m，0）在（ ）
A．x轴正半轴上B．x轴负半轴上
C．y轴正半轴上D．y轴负半轴上
6．（3分）下列计算正确的是（ ）
A．a2+a3＝a5B．a6﹣a2＝a4C．a2•a3＝a6D．（a4）3＝a12
7．（3分）如图，点E在BC的延长线上，下列条件不能判定AB∥CD的是（ ）
A．∠2＝∠4B．∠B＝∠5
C．∠5＝∠DD．∠D+∠DAB＝180°
8．（3分）下列说法正确的是（ ）
①最大的负整数是﹣1；您看到的资料都源自我们平台，20多万份试卷，家威杏 MXSJ663 每日最新，性比价最高②数轴上表示数2和﹣2的点到原点的距离相等；
③当a≤0时，|a|＝﹣a成立；
④a的倒数是；
⑤（﹣2）3与﹣23相等．
A．2个B．3个C．4个D．5个
9．（3分）如图，10块相同的长方形墙砖拼成一个矩形，设长方形墙砖的长和宽分别为x厘米和y厘米，则依题意列方程组正确的是（ ）
A．B．
C．D．
10．（3分）下列各题中，正确的是（ ）
①﹣[5a﹣（3a﹣4）]＝2a+4；
②a﹣3b+c﹣3d＝（a+c）﹣3（b+d）；
③a﹣3（b﹣c）＝a﹣3b+c；
④x﹣2（y﹣z）＝x﹣2y+2z．
A．①②B．②④C．①②④D．①③④
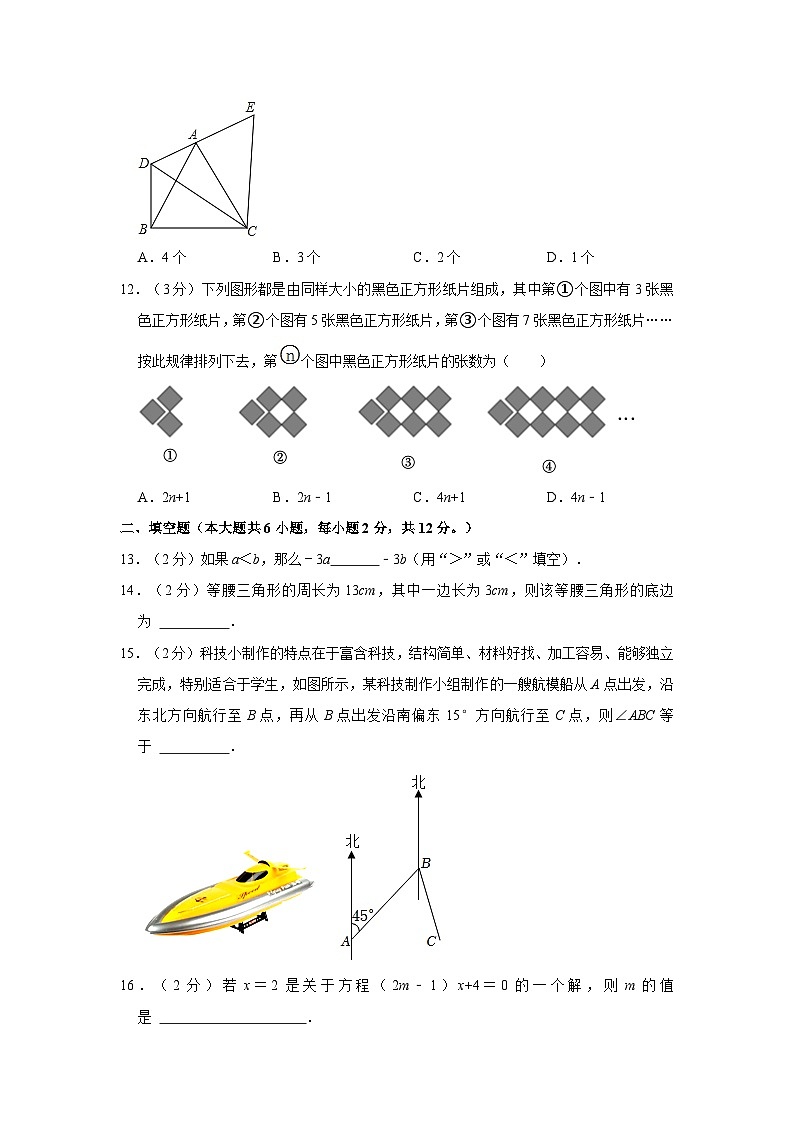
11．（3分）如图，△ABC为等边三角形，以AB为边向形外作△ABD，使∠ADB＝120°，再以点C为旋转中心把△CBD旋转到△CAE，则下列结论：
①D、A、E三点共线；
②DC平分∠BDA；
③∠E＝∠BAC；
④DC＝DB+DA．
其中正确的有（ ）
A．4个B．3个C．2个D．1个
12．（3分）下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图有5张黑色正方形纸片，第③个图有7张黑色正方形纸片……按此规律排列下去，第个图中黑色正方形纸片的张数为（ ）
A．2n+1B．2n﹣1C．4n+1D．4n﹣1
二、填空题（本大题共6小题，每小题2分，共12分。）
13．（2分）如果a＜b，那么﹣3a ﹣3b（用“＞”或“＜”填空）．
14．（2分）等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边为 ．
15．（2分）科技小制作的特点在于富含科技，结构简单、材料好找、加工容易、能够独立完成，特别适合于学生，如图所示，某科技制作小组制作的一艘航模船从A点出发，沿东北方向航行至B点，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于 ．
16．（2分）若x＝2是关于方程（2m﹣1）x+4＝0的一个解，则m的值是 ．
17．（2分）已知am＝2，an＝4，则a4m+2n的值是 ．
18．（2分）如图，在∠AOB的边OA、OB上取点M、N，连接MN，PM平分∠AMN，PN平分∠MNB，若MN＝2，△PMN的面积是2，△OMN的面积是8，则OM+ON的长是 ．
三、解答题（本大题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。）
19．（6分）计算：．
20．（6分）解方程组：．
21．（10分）如图，在△ABC中，AB＝AC，∠A的平分线交BC于点D．
（1）作AD的垂直平分线，分别交AB，AC，AD于点E，F，G．连接DE，DF．
（要求：尺规作图，不写作法，保留作图痕迹．）
（2）求证：AF＝DE．
22．（10分）某报社为了解南宁市民对大范围雾霾天气的成因、影响以及应对措施的看法，做了一次抽样调查，其中有一个问题是：“您觉得雾霾天气对您哪方面的影响最大？”五个选项分别是；
A．身体健康；
B．出行；
C．情绪不爽；
D．工作学习；
E．基本无影响．
根据调查统计结果，绘制了不完整的三种统计图表．
表1
（1）表1中本次参与调查的市民共有 人，m＝ ，n＝ ；
（2）图2所示的扇形统计图中A部分扇形所对应的圆心角是 度．
（3）请将图1的条形统计图补充完整；
（4）南宁市常住人口约900万人，试估计认为“对身体健康影响最大”的人数．
23．（10分）作图题，如图，△ABC为格点三角形（不要求写作法）
（1）作出与△ABC关于x轴对称的图形△A1B1C1；
（2）若图中一个小正方形边长为一个单位长度，请写出各点的坐标：A1 ；B1 ；C1 ；
（3）求△A1B1C1的面积．
（4）若点P为y轴上一点，使点P到B、C的距离和最小，标出点P．
24．（10分）综合与实贱：
问题情境：数学活动课上，王老师出示了一个问题：
如图1，△ABC中，AB＝AC，∠BAC＝90°，点E为△ABC 外一点，AE⊥CE，过B作BF⊥AE，垂足分别为E、F．求证：EF＝BF﹣CE．
独立思考：（1）请证明王老师提出的问题．
实践探究：（2）王老师把原题作如下的更改，并提出新问题，请你解答．
“如图2，△ABC中，AB＝AC，∠BAC＝90°，点D是BC上一点，BA＝BD，CE⊥AD 于E，求证：AD＝2CE”．
25．（10分）列方程解应用题：近年来，我市全面实行新型农村合作医疗，得到了广大农民的积极响应，很多农民看病贵、看病难的问题在合作医疗中得到了缓解．参加医保的农民可在规定的医院就医并按规定标准报销部分医疗费用，下表①是医疗费用分段报销的标准；下表②是甲、乙、丙三位农民今年的实际医疗费及个人承担总费用．
表①
表②
注明：①个人承担医疗费＝实际医疗费﹣按标准报销的金额；
②个人承担总费用包括门诊费和住院费中个人承担的部分．
请根据上述信息，解答下列问题：
（1）填空：a＝ ，b＝ ，c＝ ；
（2）李大爷去年和今年的实际住院费共计52000元，他本人共承担了18300元，已知今年的住院费超过去年，则李大爷今年实际住院费用是多少元？
26．（10分）综合与实践——探索图形平移中的数学问题
问题情境：如图1，已知△ABC是等边三角形，AB＝6，点D是AC边的中点，以AD为边，在△ABC外部作等边三角形ADE．
操作探究：将△ADE从图1的位置开始，沿射线AC方向平移，点A，D，E的对应点分别为点A′，D′，E′．
（1）如图2，善思小组的同学画出了BA'＝BD′时的情形，求此时△ADE平移的距离；
（2）如图3，点F是BC的中点，在△ADE平移过程中，连接E′F′交射线AC于点O，敏学小组的同学发现OE′＝OF始终成立！请你证明这一结论；
拓展延伸：（3）请从A，B两题中任选一题作答，我选择 题．
A．在△ADE平移的过程中，直接写出以F，A′，D′为顶点的三角形成为直角三角形时，△ADE平移的距离．
B．在△ADE平移的过程中，直接写出以F，D′，E′为顶点的三角形成为直角三角形时，△ADE平移的距离．
参考答案与试题解析
一、选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑。）
1．（3分）在1，﹣1.1，0，﹣3中，最小的数是（ ）
A．1B．﹣1.1C．0D．﹣3
【解答】解：∵|﹣3|＞|﹣1.1|，
∴﹣3＜﹣1.1＜0＜1，
∴在1，﹣1.1，0，﹣3中，最小的数是﹣3，
故选：D．
2．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（ ）
A．B．C．D．
【解答】解：A、不是轴对称图形，故本选项错误；
B、不是轴对称图形，故本选项错误；
C、不是轴对称图形，故本选项错误；
D、是轴对称图形，故本选项正确．
故选：D．
3．（3分）下列实数中，是无理数的为（ ）
A．B．3.14C．D．
【解答】解：＝2，
，3.14，是有理数；
是无理数，
故选：C．
4．（3分）如图，用不等式表示数轴上所示的解集，正确的是（ ）
A．x＜﹣1或x≥3B．x≤﹣1或x＞3C．﹣1≤x＜3D．﹣1＜x≤3
【解答】解：由图示可看出，从﹣1出发向右画出的折线且表示﹣1的点是空心圆，表示x＞﹣1；
从3出发向左画出的折线且表示3的点是实心圆，表示x≤3．
所以这个不等式组为﹣1＜x≤3
故选：D．
5．（3分）若点P（m，1）在第二象限内，则点Q（﹣m，0）在（ ）
A．x轴正半轴上B．x轴负半轴上
C．y轴正半轴上D．y轴负半轴上
【解答】解：由点P（m，1）在第二象限内，得
m＜0，
﹣m＞0，
点Q（﹣m，0）在x轴的正半轴上，
故选：A．
6．（3分）下列计算正确的是（ ）
A．a2+a3＝a5B．a6﹣a2＝a4C．a2•a3＝a6D．（a4）3＝a12
【解答】解：A、a2与a3，不是同类项不能直接合并，故本选项错误；
B、a6与a2不是同类项，不能合并，故本选项错误；
C、a2•a3＝a5，故本选项错误；
D、（a4）3＝a12，计算正确，故本选项正确；
故选：D．
7．（3分）如图，点E在BC的延长线上，下列条件不能判定AB∥CD的是（ ）
A．∠2＝∠4B．∠B＝∠5
C．∠5＝∠DD．∠D+∠DAB＝180°
【解答】解：A、根据内错角相等，两直线平行可判定AB∥CD，故此选项不合题意；
B、根据同位角相等，两直线平行可判定AB∥CD，故此选项不合题意；
C、根据内错角相等，两直线平行可判定AD∥CB，无法判定AB∥CD，故此选项符合题意；
D、根据同旁内角互补，两直线平行可判定AB∥CD，故此选项不合题意；
故选：C．
8．（3分）下列说法正确的是（ ）
①最大的负整数是﹣1；
②数轴上表示数2和﹣2的点到原点的距离相等；
③当a≤0时，|a|＝﹣a成立；
④a的倒数是；
⑤（﹣2）3与﹣23相等．
A．2个B．3个C．4个D．5个
【解答】解：①正确；
②2和﹣2的绝对值相等，则数轴上表示数2和﹣2的点到原点的距离相等，故命题正确；
③正确；
④当a≠0时，a的倒数是，故命题错误；
⑤正确．
故选：C．
9．（3分）如图，10块相同的长方形墙砖拼成一个矩形，设长方形墙砖的长和宽分别为x厘米和y厘米，则依题意列方程组正确的是（ ）
A．B．
C．D．
【解答】解：根据图示可得，
故选：B．
10．（3分）下列各题中，正确的是（ ）
①﹣[5a﹣（3a﹣4）]＝2a+4；
②a﹣3b+c﹣3d＝（a+c）﹣3（b+d）；
③a﹣3（b﹣c）＝a﹣3b+c；
④x﹣2（y﹣z）＝x﹣2y+2z．
A．①②B．②④C．①②④D．①③④
【解答】解：①﹣[5a﹣（3a﹣4）]＝﹣[5a﹣3a+4]＝﹣（2a+4）＝﹣2a﹣4，故错误；
②正确；
③a﹣3（b﹣c）＝a﹣3b+3c，故错误；
④正确．
故选：B．
11．（3分）如图，△ABC为等边三角形，以AB为边向形外作△ABD，使∠ADB＝120°，再以点C为旋转中心把△CBD旋转到△CAE，则下列结论：
①D、A、E三点共线；
②DC平分∠BDA；
③∠E＝∠BAC；
④DC＝DB+DA．
其中正确的有（ ）
A．4个B．3个C．2个D．1个
【解答】解：如图，
①设∠1＝x度，则∠2＝（60﹣x）度，∠DBC＝（x+60）度，故∠4＝（x+60）度，
∴∠2+∠3+∠4＝60﹣x+60+x+60＝180度，
∴D、A、E三点共线；
故①正确；
②∵△BCD绕着点C按顺时针方向旋转60°得到△ACE，
∴CD＝CE，∠DCE＝60°，
∴△CDE为等边三角形，
∴∠E＝60°，
∴∠BDC＝∠E＝60°，
∴∠CDA＝120°﹣60°＝60°，
∴DC平分∠BDA；
故②正确；
③∵∠BAC＝60°，
∠E＝60°，
∴∠E＝∠BAC．
故③正确；
④由旋转可知AE＝BD，
又∵∠DAE＝180°，
∴DE＝AE+AD．
∵△CDE为等边三角形，
∴DC＝DB+BA．故④正确；
故选：A．
12．（3分）下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图中有3张黑色正方形纸片，第②个图有5张黑色正方形纸片，第③个图有7张黑色正方形纸片……按此规律排列下去，第个图中黑色正方形纸片的张数为（ ）
A．2n+1B．2n﹣1C．4n+1D．4n﹣1
【解答】解：观察图形知：
第①个图中有3张黑色正方形纸片，1+2＝3，
第②个图中有5张黑色正方形纸片，1+2×2＝5，
第③个图中有7张黑色正方形纸片，1+2×3＝7，
…，
故第个图形黑色正方形纸片个数是1+2n，
故选：A．
二、填空题（本大题共6小题，每小题2分，共12分。）
13．（2分）如果a＜b，那么﹣3a ＞ ﹣3b（用“＞”或“＜”填空）．
【解答】解：在不等式a＜b的两边同时乘以﹣3，不等号的方向改变，所以﹣3a＞﹣3b．
故答案为：＞．
14．（2分）等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边为 3cm ．
【解答】解：当长是3cm的边是底边时，三边为3cm，5cm，5cm，等腰三角形成立；
当长是3cm的边是腰时，底边长是：13﹣3﹣3＝7（cm），而3+3＜7，不满足三角形的三边关系．
故底边长是：3cm．
故答案为：3cm
15．（2分）科技小制作的特点在于富含科技，结构简单、材料好找、加工容易、能够独立完成，特别适合于学生，如图所示，某科技制作小组制作的一艘航模船从A点出发，沿东北方向航行至B点，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于 60° ．
【解答】解：如图：
由题意得：
∠CBF＝15°，AE∥BF，
∴∠ABF＝∠EAB＝45°，
∴∠ABC＝∠ABF+∠CBF＝60°，
故答案为：60°．
16．（2分）若x＝2是关于方程（2m﹣1）x+4＝0的一个解，则m的值是 ．
【解答】解：把x＝2代入方程（2m﹣1）x+4＝0得，
2（2m﹣1）+4＝0，
解得：，
故答案为：．
17．（2分）已知am＝2，an＝4，则a4m+2n的值是 256 ．
【解答】解：∵am＝2，an＝4，
∴a4m+2n
＝a4m×a2n
＝（am）4×（an）2
＝24×42
＝16×16
＝256，
故答案为：256．
18．（2分）如图，在∠AOB的边OA、OB上取点M、N，连接MN，PM平分∠AMN，PN平分∠MNB，若MN＝2，△PMN的面积是2，△OMN的面积是8，则OM+ON的长是 10 ．
【解答】解：过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，
∵P是△MON外角平分线的交点，
∴PF＝PG＝PE，
∵MN＝2，△PMN的面积是2，
∴MN•PF＝2，
∴PF＝2，
∴PG＝PE＝2，
∵△OMN的面积是8，
∴△OMP的面积+△ONP的面积﹣△PMN的面积＝8，
∴OM•PG+ON•PE﹣2＝8，
∴OM+ON＝10，
故答案为：10．
三、解答题（本大题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。）
19．（6分）计算：．
【解答】解：原式＝﹣1﹣1.5××（2﹣4）
＝﹣1﹣×（﹣2）
＝﹣1+
＝﹣．
20．（6分）解方程组：．
【解答】解：①×（﹣3）+②得，17y＝17，y＝1，
将y＝1代入①得，2x﹣5＝﹣3，
解得x＝1，
∴方程组解为．
21．（10分）如图，在△ABC中，AB＝AC，∠A的平分线交BC于点D．
（1）作AD的垂直平分线，分别交AB，AC，AD于点E，F，G．连接DE，DF．
（要求：尺规作图，不写作法，保留作图痕迹．）
（2）求证：AF＝DE．
【解答】解：（1）如图所示：
直线EF为所求作的垂直平分线；
（2）证明：∵EF⊥AD，AG＝DG，
∴∠AGE＝∠AGF＝90°，AE＝DE．
∵AD平分∠BAC，
∴∠EAG＝∠FAG．
在△AEG和△AFG中，
∵∠EAG＝∠FAG，
AG＝AG，
∠AGE＝∠AGF，
∴△AEG≌△AFG（ASA）．
∴AE＝AF．
∴AF＝DE．
22．（10分）某报社为了解南宁市民对大范围雾霾天气的成因、影响以及应对措施的看法，做了一次抽样调查，其中有一个问题是：“您觉得雾霾天气对您哪方面的影响最大？”五个选项分别是；
A．身体健康；
B．出行；
C．情绪不爽；
D．工作学习；
E．基本无影响．
根据调查统计结果，绘制了不完整的三种统计图表．
表1
（1）表1中本次参与调查的市民共有 200 人，m＝ 65% ，n＝ 5% ；
（2）图2所示的扇形统计图中A部分扇形所对应的圆心角是 234 度．
（3）请将图1的条形统计图补充完整；
（4）南宁市常住人口约900万人，试估计认为“对身体健康影响最大”的人数．
【解答】解：（1）根据题意得：30÷15%＝200（人），
等级C的人数为200×10%＝20（人），
则等级A的人数为200﹣（30+20+10+10）＝130，
占的百分比为×100%＝65%，
n＝1﹣（65%+15%+10%+5%）＝5%；
故答案为：200；65%；5%；
（2）根据题意得：360°×65%＝234°；
故答案为：234；
（3）如图1所示：
（4）900×65%＝585（万人），
答：认为“对身体健康影响最大”的人数约为585万人．
23．（10分）作图题，如图，△ABC为格点三角形（不要求写作法）
（1）作出与△ABC关于x轴对称的图形△A1B1C1；
（2）若图中一个小正方形边长为一个单位长度，请写出各点的坐标：A1 （0，﹣3） ；B1 （﹣4，﹣4） ；C1 （﹣2，﹣1） ；
（3）求△A1B1C1的面积．
（4）若点P为y轴上一点，使点P到B、C的距离和最小，标出点P．
【解答】解：（1）如图，△A1B1C1即为所求；
（2）A1 （0，﹣3）；B1 （﹣4，﹣4）；C1 （﹣2，﹣1）；
故答案为：（0，﹣3），（﹣4，﹣4），（﹣2，﹣1）；
（3）△A1B1C1的面积＝3×4﹣×2×2﹣×2×3﹣×1×4＝5；
（4）如图，点P即为所求．
24．（10分）综合与实贱：
问题情境：数学活动课上，王老师出示了一个问题：
如图1，△ABC中，AB＝AC，∠BAC＝90°，点E为△ABC 外一点，AE⊥CE，过B作BF⊥AE，垂足分别为E、F．求证：EF＝BF﹣CE．
独立思考：（1）请证明王老师提出的问题．
实践探究：（2）王老师把原题作如下的更改，并提出新问题，请你解答．
“如图2，△ABC中，AB＝AC，∠BAC＝90°，点D是BC上一点，BA＝BD，CE⊥AD 于E，求证：AD＝2CE”．
【解答】（1）证明：∵CE⊥AE，BF⊥AE，
∴∠E＝∠AFB＝∠CAB＝90°，
∴∠CAE+∠EAB＝90°，∠EAB+∠ABF＝90°，
∴∠CAE＝∠ABF，
在△AEC和△BFA中，
，
∴△AEC≌△BFA（AAS），
∴EC＝AF，AE＝BF，
∴EF＝AE﹣AF＝BF﹣CE；
（2）证明：如图2中，过点B作BT⊥AE于点T．
∵BA＝BD，BT⊥AD，
∴AT＝DT，
同法可证△AEC≌△BTA，
∴EC＝AT，
∴AD＝2EC．
25．（10分）列方程解应用题：近年来，我市全面实行新型农村合作医疗，得到了广大农民的积极响应，很多农民看病贵、看病难的问题在合作医疗中得到了缓解．参加医保的农民可在规定的医院就医并按规定标准报销部分医疗费用，下表①是医疗费用分段报销的标准；下表②是甲、乙、丙三位农民今年的实际医疗费及个人承担总费用．
表①
表②
注明：①个人承担医疗费＝实际医疗费﹣按标准报销的金额；
②个人承担总费用包括门诊费和住院费中个人承担的部分．
请根据上述信息，解答下列问题：
（1）填空：a＝ 30 ，b＝ 1736 ，c＝ 80 ；
（2）李大爷去年和今年的实际住院费共计52000元，他本人共承担了18300元，已知今年的住院费超过去年，则李大爷今年实际住院费用是多少元？
【解答】解：（1）甲的门诊费为260元，个人承担为182元，
所以有260（1﹣a%）＝182，
解得a＝30，
乙个人承担费用为：b＝80×（1﹣30%）+2800×（1﹣40%）＝1736（元），
根据题意丙个人承担费用为：400×（1﹣30%）+5000×（1﹣40%）+（20000﹣5000）×（1﹣50%）+（25000﹣20000）（1﹣c%）＝11780，
解得c＝80．
故答案为：30，1736，80；
（2）由表可知当住院费用为20000元时，其个人承担费用5000×60%+15000×50%＝10500元，而李大爷两年总承担为18300元，故去年的费用低于20000元，
当如果去年住院费用为5000元时，其个人承担费用为3000元，
则今年的为52000﹣5000＝47000元，个人承担费用为：5000×60%+15000×50%+27000×20%＝15900元，
此时住院费用为15900+3000＝18900＞18300，
故李大爷去年住院费用小于5000元，
设今年住院费用为x元，则去年住院费用为（52000﹣x）元，
根据题意可得：（52000﹣x）×60%+5000×60%+15000×50%+（x﹣20000）×20%＝18300，
解得x＝48500．
所以李大爷今年实际住院费用为48500元．
26．（10分）综合与实践——探索图形平移中的数学问题
问题情境：如图1，已知△ABC是等边三角形，AB＝6，点D是AC边的中点，以AD为边，在△ABC外部作等边三角形ADE．
操作探究：将△ADE从图1的位置开始，沿射线AC方向平移，点A，D，E的对应点分别为点A′，D′，E′．
（1）如图2，善思小组的同学画出了BA'＝BD′时的情形，求此时△ADE平移的距离；
（2）如图3，点F是BC的中点，在△ADE平移过程中，连接E′F′交射线AC于点O，敏学小组的同学发现OE′＝OF始终成立！请你证明这一结论；
拓展延伸：（3）请从A，B两题中任选一题作答，我选择 A（或B） 题．
A．在△ADE平移的过程中，直接写出以F，A′，D′为顶点的三角形成为直角三角形时，△ADE平移的距离．
B．在△ADE平移的过程中，直接写出以F，D′，E′为顶点的三角形成为直角三角形时，△ADE平移的距离．
【解答】（1）解：连接BD，如图：
∵△ABC是等边三角形，AB＝6，点D是AC边的中点，
∴AD＝3＝CD，BD⊥AC，
∵将△ADE从图1的位置开始，沿射线AC方向平移，点A，D，E的对应点分别为点A′，D′，E′，
∴A'D'＝AD＝3，
∵A'B＝BD'，BD⊥AC，
∴A'D＝DD'＝A'D'＝，
∴△ADE平移的距离DD'为；
（2）证明：如图：
∵△ADE是等边三角形，AD＝3，
∴∠DAE＝60°，AE＝3，
∵将△ADE从图1的位置开始，沿射线AC方向平移，点A，D，E的对应点分别为点A′，D′，E′，
∴∠D'A'E'＝∠DAE＝60°，A'E'＝3，
∵△ABC是等边三角形，AB＝6，点F是BC边的中点，
∴∠ACB＝60°，CF＝BC＝3，
∴∠D'A'E'＝∠ACB＝60°，A'E'＝CF＝3，
∵∠A'OE'＝∠COF，
∴△A'OE'≌△COF（AAS），
∴OE'＝OF；
（3）解：选择A（或B）题：
选A：
当∠A'D'F＝90°时，如图：
∴∠CD'F＝90°，
∵∠C＝60°，
∴∠D'FC＝30°，
∴CD'＝CF＝，
∴DD'＝CD﹣CD'＝3﹣＝；
∴△ADE平移的距离是；
当∠FA'D'＝90°时，如图：
同理可得A'C＝，
∴AA'＝AC﹣A'C＝6﹣＝；
∴△ADE平移的距离是；
综上所述，以F，A′，D′为顶点的三角形成为直角三角形时，△ADE平移的距离是或；
选B：
当A'与C重合时，如图：
∵△A'D'E'是等边三角形，
∴∠E'A'D'＝∠A'D'E'＝∠E'＝60°，
∵A'F＝A'D'＝3，
∴∠A'FD'＝∠A'D'F＝30°，
∴∠FD'E'＝∠A'D'F+∠A'D'E'＝90°，即以F，D′，E′为顶点的三角形成为直角三角形，
此时DD'＝CD+A'D'＝3+3＝6，
∴△ADE平移的距离是6；
当∠D'E'F＝90°时，如图：
∵∠A'E'D'＝60°＝∠E'A'D'，
∴∠A'E'O＝∠D'E'F﹣∠A'E'D'＝30°，
∴∠A'OE'＝∠D'A'E'﹣∠A'E'O＝30°，
∴∠A'E'O＝∠A'OE'，
∴A'O＝A'E'＝3，
由（2）知△A'OE'≌△COF，
∴CO＝A'O＝3，
∴DD'＝CD+CO+A'O+A'D'＝3+3+3+3＝12，
∴△ADE平移的距离是12；
综上所述，以F，D′，E′为顶点的三角形成为直角三角形时，△ADE平移的距离是6或12．雾霾天气对您哪方面的影响最大
百分比
A．身体健康
m
B．出行
15%
C．情绪不爽
10%
D．工作学习
n
E．基本无影响
5%
医疗费用范围
门诊费
住院费（元）

0～5000
的部分
5000～20000
的部分
20000以上的部分
报销比例
a%
40%
50%
c%


门诊费
住院费
个人承担总费用
甲
260元
0元
182元
乙
80元
2800元
b元
丙
400元
25000元
11780元
雾霾天气对您哪方面的影响最大
百分比
A．身体健康
m
B．出行
15%
C．情绪不爽
10%
D．工作学习
n
E．基本无影响
5%
医疗费用范围
门诊费
住院费（元）

0～5000
的部分
5000～20000
的部分
20000以上的部分
报销比例
a%
40%
50%
c%


门诊费
住院费
个人承担总费用
甲
260元
0元
182元
乙
80元
2800元
b元
丙
400元
25000元
11780元