2024版高考数学全程学习复习导学案第一章集合与常用逻辑用语第一节集合课件

这是一份2024版高考数学全程学习复习导学案第一章集合与常用逻辑用语第一节集合课件，共50页。PPT课件主要包含了知识梳理·思维激活，确定性，互异性，不属于，列举法，描述法，N或N+，A⊆B或B⊇A，A⫋B或B⫌A，集合的基本运算等内容，欢迎下载使用。

【课程标准】1.通过实例,了解集合的含义,理解元素与集合的属于关系.2.针对具体问题,能在自然语言和图形语言的基础上,用符号语言刻画集合.3.在具体情境中,了解全集与空集的含义.4.理解集合之间包含与相等的含义,能识别给定集合的子集.5.理解两个集合的并集与交集的含义,能求两个集合的并集与交集.6.理解在给定集合中一个子集的补集的含义,能求给定子集的补集.7.能使用Venn图表达集合的基本关系与基本运算,体会图形对理解抽象概念的作用.
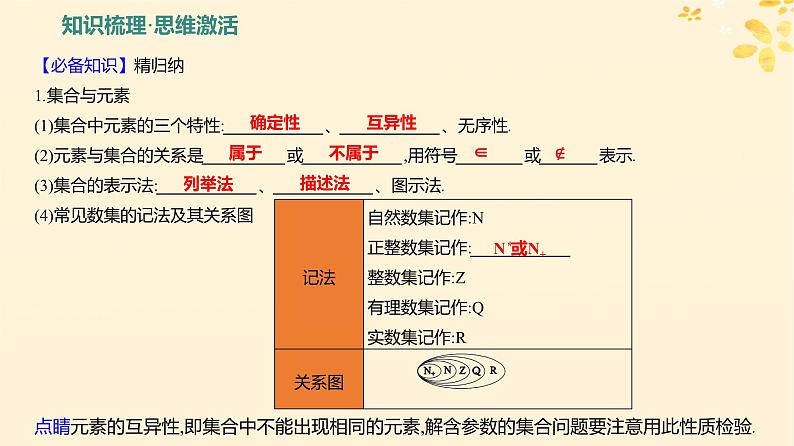
【必备知识】精归纳1.集合与元素(1)集合中元素的三个特性:____________、____________、无序性. (2)元素与集合的关系是__________或____________,用符号________或_______表示. (3)集合的表示法:____________、____________、图示法. (4)常见数集的记法及其关系图点睛元素的互异性,即集合中不能出现相同的元素,解含参数的集合问题要注意用此性质检验.
2.集合间的基本关系点睛0,{0},⌀,{⌀}之间的关系:⌀≠{⌀},⌀∈{⌀},⌀⊆{⌀},0∉⌀,0∉{⌀},0∈{0},⌀⊆{0}.
【基础小题】固根基1.(忽视互异性)若a∈{1,3,a2},则a的可能取值有(　　)A.1,3B.0,1C.0,3D.0,1,3【解析】集合元素要满足互异性,a=0时,该集合为{1,3,0},符合;a=3时,该集合为{1,3,9},符合;其他均不符合.
4.(结论2)已知集合A={1,3,a2},B={1,a+2},若A∩B=B,则实数a的取值为(　　)A.1B.-1或2C.2D.-1或1
5.(忽略空集)集合A={-1,2},B={x|ax-2=0},若B⊆A,则由实数a组成的集合为(　　)A.{-2}B.{1}C.{-2,1}D.{-2,1,0}【解析】因为集合A={-1,2},B={x|ax-2=0},B⊆A,所以B=⌀或B={-1}或B={2},所以a=0,1,-2.所以由实数a组成的集合为{-2,1,0}.
6.(教材提升)设集合A={(x,y)|x+y=1},B={(x,y)|x-y=3},则A∩B=　　　　　. 答案:{(2,-1)}
【题型一】集合的基本概念[典例1](1)(2022·聊城模拟)已知集合A={0,1,2},B={ab|a∈A,b∈A},则集合B中元素个数为(　　)A.2B.3C.4D.5
(2)(2022·南京模拟)设集合M={5,x2},N={5x,5}.若M=N,则实数x的值组成的集合为(　　)A.{5}B.{1}C.{0,5}D.{0,1}【解析】因为集合M={5,x2},N={5x,5},M=N,所以x2=5x,x=0或5,所以x的值组成的集合为{0,5}.
(3)(多选题)已知集合A={x|x=3k+1,k∈Z},则下列表示正确的是(　　)A.-2∈AB.2 023∈AC.3k2+1∉AD.-35∉A
【方法提炼】——自主完善,老师指导求解与集合的基本概念有关问题的关键点(1)用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是数集、__________,还是其他类型的集合; (2)含有字母的集合,在求出字母的值后,要注意检验集合中的元素是否满足______________. 
【对点训练】1.(2022·南通模拟)已知集合A={(x,y)||x|+|y|≤2,x∈Z,y∈Z},则A中元素的个数为(　　)A.9B.10C.12D.13【解析】选由题意可知,集合A中的元素有(-2,0),(-1,-1),(-1,0),(-1,1),(0,-2),(0,-1),(0,0),(0,1),(0,2),(1,-1),(1,0),(1,1),(2,0),共13个.
2.设集合A={x|3x-1【加练备选】1.已知集合P={x|x=2k,k∈Z},Q={x|x=2k+1,k∈Z},M={x|x=4k+1,k∈Z},且a∈P,b∈Q,则(　　)A.a+b∈PB.a+b∈QC.a+b∈MD.a+b不属于P,Q,M中的任意一个
3.已知集合A={a+2,(a+1)2,a2+3a+3},若1∈A,则2 020a的值为　　;若1∉A,则a不可能取得的值为　　　. 
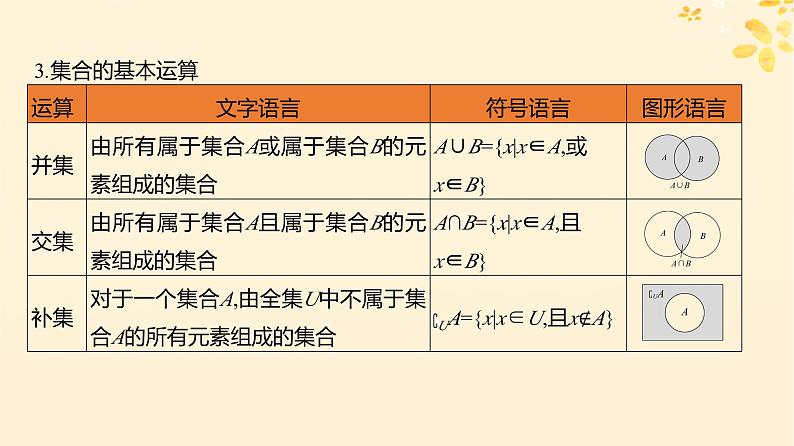
【题型二】集合间的基本关系[典例2](1)设全集U=R,则集合M={0,1,2}和N={x|x·(x-2)·lg2x=0}的关系可表示为(　　)【解析】因为N={x|x·(x-2)·lg2x=0}={1,2},M={0,1,2},所以N是M的真子集.
(3)(2023·枣庄模拟)已知集合A={y|y=2cs x,x∈R},满足B⫋A的集合B可以是(　　)A.[-2,2]B.[-2,3]C.[-1,1]D.R【解析】A={y|y=2cs x,x∈R}=[-2,2],且B⫋A,结合选项知,C项符合题意.
(4)(2022·舟山模拟)若集合A={x|2a+1≤x≤3a-5},B={x|5≤x≤16},则能使A⊆B成立的所有a组成的集合为(　　)A.{a|2≤a≤7}B.{a|6≤a≤7}C.{a|a≤7}D.⌀
【方法提炼】——自主完善,老师指导1.判断集合间关系的三种方法(1)列举法:由题中条件表示集合元素,然后比较集合元素的异同,找出集合之间的关系.(2)特征分析法:从元素满足的共同特征入手,结合______、配方等变形技巧,找出集合之间的关系.(3)数轴法:在同一个数轴上表示出两个集合,比较______之间的大小关系,从而确定集合与集合之间的关系.
2.根据两集合的关系求参数的方法(1)若集合元素是一一列举的,依据集合间的关系,转化为解方程(组)求解,此时注意集合中元素的互异性.(2)若集合表示的是不等式的解集,常依据数轴转化为不等式(组)求解,此时需注意端点值能否取到.提醒若有条件B⊆A,则应注意判断是否需要分B=∅和B≠∅两种情况进行讨论.
【对点训练】1.设集合P={y|y=x2+1},M={x|y=x2+1},则集合M与集合P的关系是(　　)A.M=PB.P∈MC.M⊆PD.P⊆M【解析】因为P={y|y=x2+1}={y|y≥1},M={x|y=x2+1}=R,因此P⊆M.
【加练备选】1.已知集合A={x∈R|x2-3x+2=0},B={x∈N|02.已知集合A={x|x2-2 023x+2 022<0},B={x|x角度3　根据集合的运算结果求参数[典例5](1)(2023·常德模拟)已知集合A={x∈Z|x2≤1},B={x|x2-mx+2=0},若A∩B={1},则A∪B=(　　)A.{-1,0,1}B.{x|-1≤x≤1}C.{-1,0,1,2}D.{x|-1≤x≤2}【解析】集合A={x∈Z|x2≤1}={-1,0,1},B={x|x2-mx+2=0},A∩B={1},所以1∈B,所以1-m+2=0,解得m=3,所以B={x|x2-3x+2=0}={1,2},所以A∪B={-1,0,1,2}.
(2)(2022·龙岩模拟)已知集合A={x|x2}【解析】因为B={x|1【方法提炼】——自主完善,老师指导解集合运算问题的两种基本方法(1)若集合中的元素是连续的实数,一般利用______解决,要注意端点值能否取到,一般可将端点值代入验证.(2)根据题目特点,灵活运用_______图求解.
【加练备选】1.(2021·新高考Ⅰ卷)设集合A={x|-22.已知集合A={x|x2≥4},B={m}.若A∪B=A,则m的取值范围是 (　　)A.(-∞,-2)B.[2,+∞)C.[-2,2]D.(-∞,-2]∪[2,+∞)【解析】因为A∪B=A,所以B⊆A,即m∈A,得m2≥4,解得m≥2或m≤-2.
【备选题型】集合的新定义问题[典例]已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为　　　　. 答案:45
【备选题型】解决集合的新定义问题要注意两个关键点(1)准确转化,即解决新定义问题时,首先要读懂题意,对题目进行恰当转化,切忌与已有概念混淆;(2)方法选取,即对于新定义问题,可恰当选用特例法、筛选法等方法,并结合集合的相关性质求解.
【对点训练】若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)是集合A的同一种分拆.若集合A有三个元素,则集合A的不同分拆种数是　　　　　. 答案:27【解析】不妨令A={1,2,3},因为A1∪A2=A,当A1=⌀时,A2={1,2,3},当A1={1}时,A2可以为{2,3},{1,2,3}共2种,同理A1={2},{3}时,A2各有2种,当A1={1,2}时,A2可以为{3},{1,3},{2,3},{1,2,3}共4种,同理A1={1,3},{2,3}时,A2各有4种,当A1={1,2,3}时,A2可以为A1的子集,共8种,故共有1+2×3+4×3+8=27(种)不同的分拆.