2023-2024学年苏科版七年级上学期数学期末培优提高卷（含答案解析）

这是一份2023-2024学年苏科版七年级上学期数学期末培优提高卷（含答案解析），共14页。试卷主要包含了考试范围等内容，欢迎下载使用。
姓名：_________班级：_________学号：_________
注意事项：
1．考试范围：苏科版数学上册第1-6章，考试时间：120分钟，试卷满分：100分。答卷前，考生务必用黑色签字笔将准考证号、姓名、考场号和座位号填写在答题卡上。用 2B 铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号。将条形码粘贴在答题卡“条形码粘贴处”。
2．作答选择题时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。
3．非选择题必须用黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4．考试结束后，将本试卷和答题卡一并交回。
一、选择题（共10小题，满分20分，每小题2分）
1．（2分）（2023•模拟）在﹣2.5，﹣2，0，这四个数中最小的数是（ ）
A．﹣2.5B．﹣2C．0D．
2．（2分）（2022•一模）国务院新闻办公室2021年4月6日发布《人类减贫的中国实践》白皮书指出，改革开放以来，按照现行贫困标准计算，中国7.7亿农村贫困人口摆脱贫困，6098万贫困人口参加了城乡居民基本养老保险．将6098万用科学记数法表示为（ ）
A．6.098×103B．0.6098×104C．6.098×107D．6.098×108
3．（2分）下列说法中，正确的是（ ）
A．的系数是B．的系数是
C．3x2的系数是3D．﹣5x2的系数为5
4．（2分）根据等式的性质，下列变形正确的是（ ）
A．如果2x＝3，那么B．如果x＝y，那么x﹣5＝5﹣y
C．如果x＝y，那么﹣2x＝﹣2yD．如果x＝6，那么x＝3
5．（2分）若关于x的方程x+3k＝2的解是非负数，则k的取值范围是（ ）
A．k＞B．k≥C．k＜D．k≤
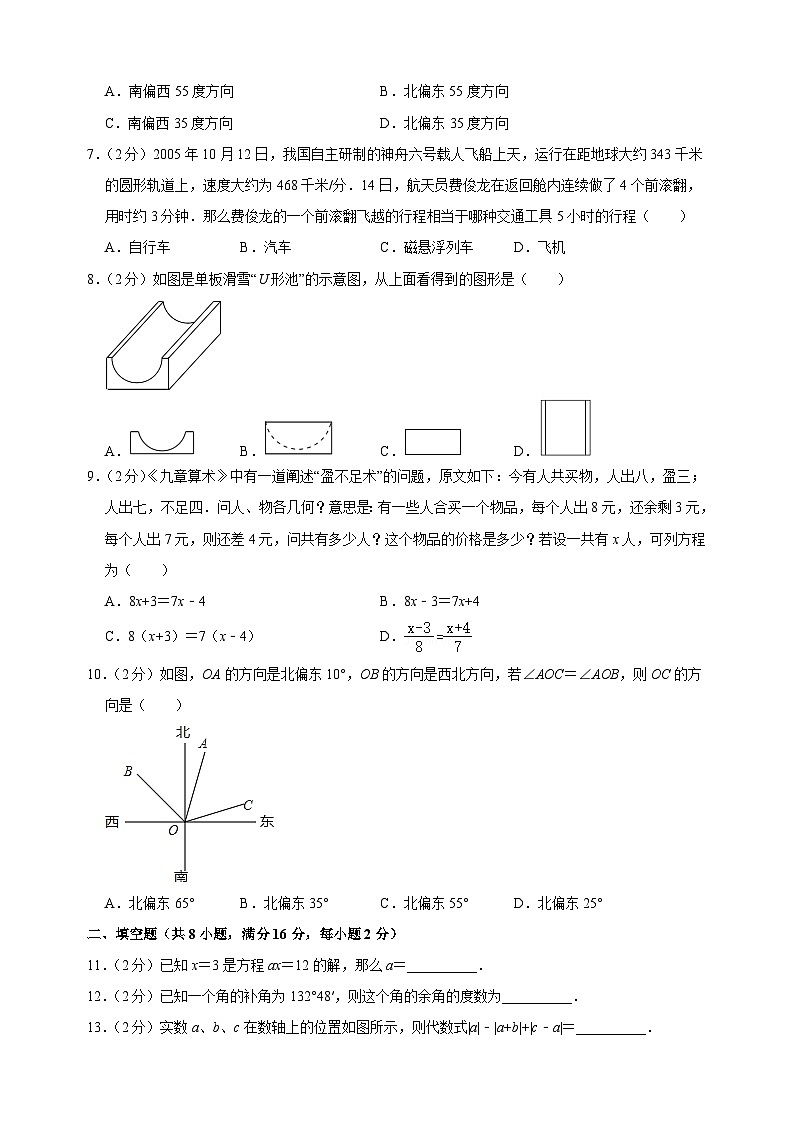
6．（2分）小明家位于学校的北偏东35度方向，那么学校位于小明家的（ ）
A．南偏西55度方向B．北偏东55度方向
C．南偏西35度方向D．北偏东35度方向
7．（2分）2005年10月12日，我国自主研制的神舟六号载人飞船上天，运行在距地球大约343千米的圆形轨道上，速度大约为468千米/分．14日，航天员费俊龙在返回舱内连续做了4个前滚翻，用时约3分钟．那么费俊龙的一个前滚翻飞越的行程相当于哪种交通工具5小时的行程（ ）
A．自行车B．汽车C．磁悬浮列车D．飞机
8．（2分）如图是单板滑雪“U形池”的示意图，从上面看得到的图形是（ ）
A．B．C．D．
9．（2分）《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四．问人、物各几何？意思是：有一些人合买一个物品，每个人出8元，还余剩3元，每个人出7元，则还差4元，问共有多少人？这个物品的价格是多少？若设一共有x人，可列方程为（ ）
A．8x+3＝7x﹣4B．8x﹣3＝7x+4
C．8（x+3）＝7（x﹣4）D．
10．（2分）如图，OA的方向是北偏东10°，OB的方向是西北方向，若∠AOC＝∠AOB，则OC的方向是（ ）
A．北偏东65°B．北偏东35°C．北偏东55°D．北偏东25°
二、填空题（共8小题，满分16分，每小题2分）
11．（2分）已知x＝3是方程ax＝12的解，那么a＝__________．
12．（2分）已知一个角的补角为132°48′，则这个角的余角的度数为__________．
13．（2分）实数a、b、c在数轴上的位置如图所示，则代数式|a|﹣|a+b|+|c﹣a|＝__________．
14．（2分）要使代数式的值为非负数，则x的最小整数解是__________．
15．（2分）如图，点E，F分别在长方形ABCD的边AD，CD上，连接BE．将长方形ABCD沿BE对折，点A落在A′处；将∠DEA′对折，点D落在EA′的延长线上的D′处，得到折痕EF，若∠BEA′＝70°，∠FED′＝__________．
16．（2分）甲种蔬菜保鲜的适宜温度（单位：℃）是1≤t≤5，乙种蔬菜保鲜的适宜温度是3≤t≤8，将这两种蔬菜放在一起同时保鲜，则保鲜的适宜温度t（单位：℃）的范围是__________．
17．（2分）（2022秋•益阳期末）如图，C，D是线段AB上的两点，E是AC的中点，F是BD的中点，若EF＝m，CD＝n，则AB＝__________．
18．（2分）（2023春•校级月考）图中各正方形中的四个数之间都有相同的规律，则根据这种规律，第四个正方形中的n与最后一个正方形中的m之和，n+m＝__________．
三、解答题（共10小题，满分64分）
19．（6分）计算：
（1）24+（﹣14）+（﹣16）+8； （2）（﹣81）÷×÷（﹣8）．
20．（5分）（2023春•肇东市期末）“计算（2x3﹣3x2y﹣2xy2）﹣（x3﹣2xy2+y3）+（﹣x3+3x2y﹣y3）的值，其中x＝，y＝﹣1”．甲同学把“x＝”错抄成“x＝﹣”，但他计算的最后结果，与其他同学的正确结果都一样．试说明理由，并求出这个结果
21．（8分）（2023春•潞城区校级期末）（1）解方程：．
（2）小明解不等式的过程如下，请认真阅读并完成相应任务．
解：去分母，得1﹣3（x+1）≤2（x﹣1），…第一步
去括号，得1﹣3x﹣3≤2x﹣2，…第二步
移项，得﹣3x﹣2x≤﹣2﹣1+3，…第三步
合并同类项，得﹣5x≤0，…第四步
系数化为1，得x≥0．…第五步
任务一：①以上求解过程中，去分母是依据__________进行变形的．
A．等式的基本性质B．分式的基本性质C．不等式的性质
②第__________步开始出现错误，错误的原因是____________________．
任务二：该不等式的正确解集是__________．
任务三：请你根据平时的学习经验，就解不等式需要注意的事项给其他同学提一条建议．
22．（6分）（2022春•洮北区期末）如图，在边长为1个单位的正方形网格中，△ABC经过平移后得到△A'B'C'，点B的对应点为点B'．
（1）画出A′B′C′，线段AC扫过的图形的面积为__________；
（2）在AB的右侧找到一个格点Q，使△ABQ的面积和△ABC的面积相等．
23．（5分）如图，直线AB和CD相交于点O，若∠BOD＝40°，OA平分∠EOC，求∠EOD的度数．
24．（6分）已知M＝3a2﹣2ab+b2，N＝2a2+ab﹣3b2．
（1）化简2M﹣3N；
（2）若2（7a﹣1）2+3|b+1|＝0，求2M﹣3N的值．
25．（8分）我们学习过了有理数的五种运算和研究运算的方法，现在定义了一个新运算：a⊗b＝■，定义的内容被遮盖住了，根据下面各式，回答问题：
观察下列式子：
1⊗3＝1×4+3＝7；
3⊗（﹣1）＝3×4﹣1＝11；
（﹣8）⊗5＝（﹣8）⊗4+5＝﹣27；
（﹣4）⊗（﹣3）＝（﹣4）×4﹣3＝﹣19．
（1）请你补全定义内容：a⊗b＝__________；（用含a、b的代数式表示）
（2）当a≠b时，这种新定义的运算是否满足交换律，即a⊗b＝b⊗a是否成立，请说明理由；
（3）如果a⊗（﹣6）＝3⊗a，请求出a的值．
26．（6分）某文艺团体为“希望工程”募捐组织了一场义演，共售出1000张票，筹出票款6920元，且每张成人票8元，学生票5元．
（1）问成人票与学生票各售出多少张？
（2）若票价不变，仍售出1000张票，所得的票款可能是7290元吗，为什么？
27．（6分）（2022秋•江岸区期末）某种包装盒的形状是长方体，长AD比高AE的三倍多2，宽AB的长度为3分米，它的展开图如图所示．（不考虑包装盒的黏合处）
（1）设该包装盒的高为m，则该长方体的长为__________分米，边FG的长度为__________分米；（用含m的式子表示）
（2）若FG的长为12分米，现对包装盒外表面涂色，每平方分米涂料的价格是6元，求为每个包装盒涂色的费用是多少？（注：包装盒内壁不涂色）
28．（8分）（2022秋•高新区期末）两个完全相同的长方形ABCD、EFGH，如图所示放置在数轴上．
（1）长方形ABCD的面积是__________。
（2）若点P在线段BE上，且PA+PB＝5，求点P在数轴上表示的数。
（3）若长方形ABCD、EFGH分别以每秒2个单位长度、1个单位长度在数轴上相向而行。设两个长方形重叠部分的面积为S，移动时间为t。
①在整个运动过程中，S的最大值是__________，持续时间是__________；
②当S是长方形ABCD面积一半时，求t的值。
参考答案
一、选择题（共10小题，满分20分，每小题2分）
1．A
解：∵2.5＞2，∴﹣2.5＜﹣2，∴﹣2.5＜﹣2＜0＜，∴最小的数是﹣2.5，故选：A．
2．C
解：6098万＝60980000＝6.098×107．故选：C．
3．C
解：A、的系数是π，故原说法不正确，选项A不符合题意；
B、xy2的系数是，故原说法不正确，选项B不符合题意；
C、3x2的系数是3，故原说法正确，选项C符合题意；
D、﹣5x2的系数为﹣5，故原说法不正确，选项D不符合题意；
故选：C．
4．C
解：A、如果2x＝3，那么，（a≠0），故此选项错误；
B、如果x＝y，那么x﹣5＝y﹣5，故此选项错误；
C、如果x＝y，那么﹣2x＝﹣2y，正确；
D、如果x＝6，那么x＝12，故此选项错误；
故选：C．
5．D
解：x+3k＝2，
x＝2﹣3k，
∵关于x的方程x+3k＝2的解是非负数，
∴2﹣3k≥0，
解得：k≤．故选：D．
6．C
解：如图所示：
∵小明家位于学校的北偏东35度方向，∴∠1＝35°，
∵∠1＝∠2，∴∠2＝35°，∴学校位于小明家南偏西35度方向；故选：C．
7．B
解：根据题意可知，分×468千米/分＝351千米，351千米÷5小时＝70.2千米/时．70.2千米/时相当于汽车的速度．故选：B．
8．D
解：由题意知，单板滑雪“U形池”的俯视图为：故选：D．
9．B
解：由题意，得：8x﹣3＝7x+4．故选：B．
10．A
解：∠AOB＝45°+10°＝55°，则∠AOC＝∠AOB＝55°，OC与正北方向的夹角是55+10＝65°．
则OC在北偏东65°．故选：A．
二、填空题（共8小题，满分16分，每小题2分）
11． 4 ．
解：由题意得，3a＝12．
∴a＝4．
故答案为：4．
12． 42°48′ ．
解：设这个角为x°，则补角为（180°﹣x°），余角为（90°﹣x°），
由题意得，180°﹣x°＝132°48′，
解得：x°＝47°12′，
∴90°﹣47°12′＝42°48′．
即这个角的余角的度数为42°48′．
故答案为：42°48′．
13． ﹣a+b+c． ．
解：由数轴上点的位置得：b＜a＜0＜c，
∴a＜0，a+b＜0，c﹣a＞0，
则|a|﹣|a+b|+|c﹣a|＝﹣a+a+b+c﹣a＝﹣a+b+c．
故答案为：﹣a+b+c．
14． ﹣2 ．
解：由题意得：≥0，
∴x+2≥0，
∴x≥﹣2，
∴x的最小整数解是﹣2．
故答案为：﹣2．
15． 20° ．
解：由翻折的性质可知：∠BEA＝∠BEA′＝70°，∠DEF＝∠FED′，
∠BEF＝∠BEA′+∠FED′＝∠AEA′+∠DED′＝×180°＝90°．
∴∠FED′＝90°﹣∠BEA′＝90°﹣70°＝20°．
故答案为：20°．
16． 3≤t≤5
解：根据题意可知，
解得3≤t≤5．
故答案为：3≤t≤5．
17． 2m﹣n ．
解：由题意得，EC+FD＝m﹣n，
∵E是AC的中点，F是BD的中点，
∴AE+FB＝EC+FD＝EF﹣CD＝m﹣n，
又∵AB＝AE+FB+EF，
∴AB＝m﹣n+m＝2m﹣n，
故答案为：2m﹣n．
18． 222 ．
解：根据前三个正方形的规律可知，左上、左下、右上为相邻的三个偶数，
所以n＝10；
最后一个正方形中，左下、右上两数分别为14、16，
所以m＝14×16﹣12＝212；
所以n+m＝222，
故答案为：222．
三、解答题（共10小题，满分64分）
19．
解：（1）24+（﹣14）+（﹣16）+8
＝24﹣14﹣16+8
＝32﹣30
＝2；
（2）（﹣81）÷×÷（﹣8）
＝81×××
＝2．
20．
解：原式＝2x3﹣3x2y﹣2xy2﹣x3+2xy2﹣y3﹣x3+3x2y﹣y3
＝﹣2y3，
由结果可知：化简结果与x无关，所以答案一样，
所以原式＝2．
21．
解：（1），
去分母，得：2（x﹣4）＝15x，
去括号，得：2x﹣8＝15x，
移项，得2x﹣15x＝8，
合并同类项，得：﹣13x＝8，
系数化为1，得：；
（2）任务一：①以上求解过程中，去分母是依据不等式的性质进行变形的，
故选：C；
②第一步开始出现错误，错误的原因是去分母时，1漏乘6，
故答案为：一；去分母时，1漏乘6；
任务二：，
去分母，得：6﹣3（x+1）≤2（x﹣1），
去括号，得：6﹣3x﹣3≤2x﹣2，
移项及合并同类项，得：﹣5x≤﹣5，
系数化为1，得：x≥1，
故答案为：x≥1；
任务三：答案不唯一．建议一：去分母时，各项都要乘分母的最小公倍数；建议二：移项时注意变号．
22．
解：（1）如图，△A′B′C′即为所求，线段AC扫过的图形的面积＝四边形CTC′A′的面积＝10×1＝10．
故答案为：10；
（2）如图，点P即为所求（答案不唯一，图中的黑点，都满足条件）．
23．
解：∵∠BOD＝40°，
∴∠AOC＝∠BOD＝40°．
∵OA平分∠EOC，
∴∠COE＝2∠AOC＝80°．
∴∠EOD＝180°﹣∠COE＝180°﹣80°＝100°．
24．
解：（1）2M﹣3N
＝2（3a2﹣2ab+b2）﹣3（2a2+ab﹣3b2）
＝6a2﹣4ab+2b2﹣6a2﹣3ab+9b2
＝﹣7ab+11b2．
（2）∵（7a﹣1）2≥0，|b+1|≥0，
∴当2（7a﹣1）2+3|b+1|＝0时，7a﹣1＝0，b+1＝0．
∴a＝，b＝﹣1，
∴2M﹣3N＝﹣7ab+11b2＝﹣7×+11×（﹣1）2＝12．
25．
解：（1）根据题意知：a⊗b＝4a+b；
故答案为：4a+b；
（2）a⊗b＝b⊗a不成立，理由如下：
由（1）知，a⊗b＝4a+b．
b⊗a＝4b+a．
当a⊗b＝b⊗a时，4a+b＝4b+a，
此时a＝b，与a≠b相矛盾，
所以a⊗b＝b⊗a不成立；
（3）由a⊗（﹣6）＝3⊗a得，4a﹣6＝3×4+a．
解得a＝6．
26．
根据题意列方程得：
8x+5（1000﹣x）＝6920，
解得：x＝640张．
∴1000﹣x＝360张．
故成人票640张，学生票360张．
（2）解：设成人票x张，则学生票就是1000﹣x张，
根据题意列方程得：
8x+5（1000﹣x）＝7290，
解得：x＝763.33333．
票都是整张卖的，所以不可能．
27．
解：（1）∵长AD比高AE的三倍多2，高AE＝m，
∴则该长方体的长为（3m+2）分米，边FG的长度为（8m+4）分米；
故答案为：（3m+2），（8m+4）；
（2）∵FG的长为12分米，
∴8m+4＝12，
解得m＝1，
∴AD＝5分米，AE＝1分米，
∴长方体的表面积为2×1×5+2×1×3+2×3×5＝46（平方分米），
∴6×46＝276（元），
答：每个包装盒涂色的费用是276元．
28．
解：（1）由图形可得：EF＝5﹣2＝3，AB＝﹣1﹣（﹣5）＝4，
∵两个完全相同的长方形ABCD、EFGH，
∴AD＝EF＝3，
∴长方形ABCD的面积是3×4＝12；
故答案为：12；
（2）设点P在数轴上表示的数是x，
则PA＝x﹣（﹣5）＝x+5，PB＝x﹣（﹣1）＝x+1，
因为PA+PB＝5，
所以（x+5）+（x+1）＝5，
解得x＝﹣，
答：点P在数轴上表示的数是﹣；
（3）①整个运动过程中，S的最大值是3×3＝9，
当点B与F重合时，（2﹣1）t＝6，解得：t＝6，
当点A与E重合时，（2﹣1）t＝7，解得：t＝7，
∴7﹣6＝1，
∴整个运动过程中，S的最大值是9，持续时间是1秒；
故答案为：9；1；
②由题意知移动t秒后，
情况一：当点B在E、F之间时，BF＝1时，重叠部分的面积为6，
此时（2﹣1）t＝5
解得t＝5，
情况二：当点A在E、F之间时，AE＝1时，重叠部分的面积为6，
此时（2﹣1）t＝8，
解得t＝8，
综上所述，当S是长方形ABCD面积一半时，t＝5或8