第2章 一元一次不等式和一元一次不等式组（回顾与思考） 北师大版八年级数学下册同步教学课件

这是一份第2章 一元一次不等式和一元一次不等式组（回顾与思考） 北师大版八年级数学下册同步教学课件，共32页。

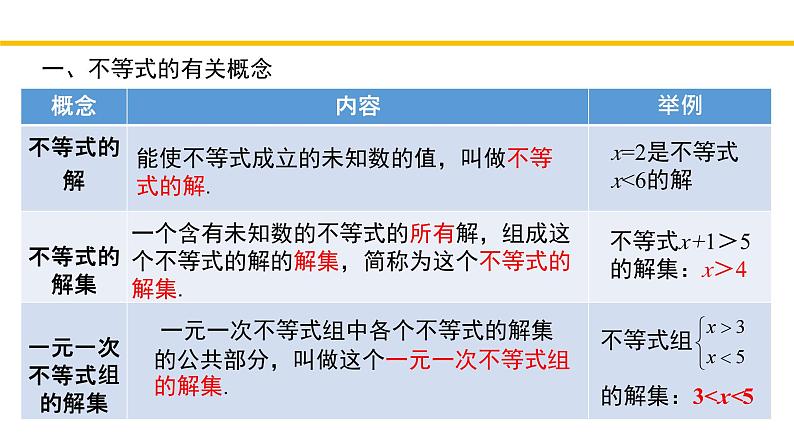
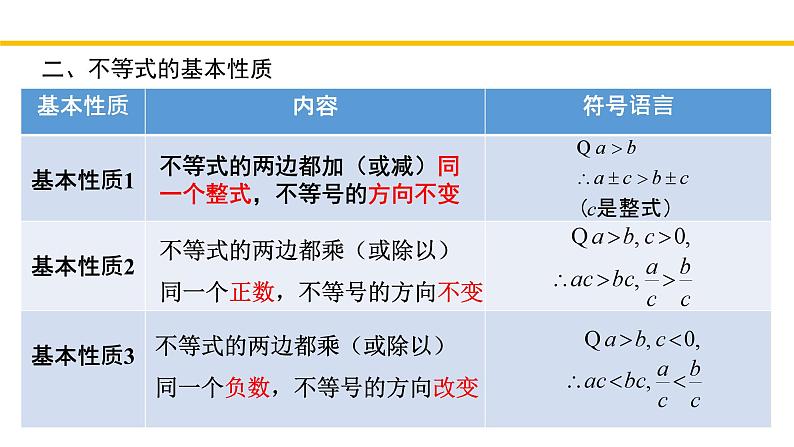
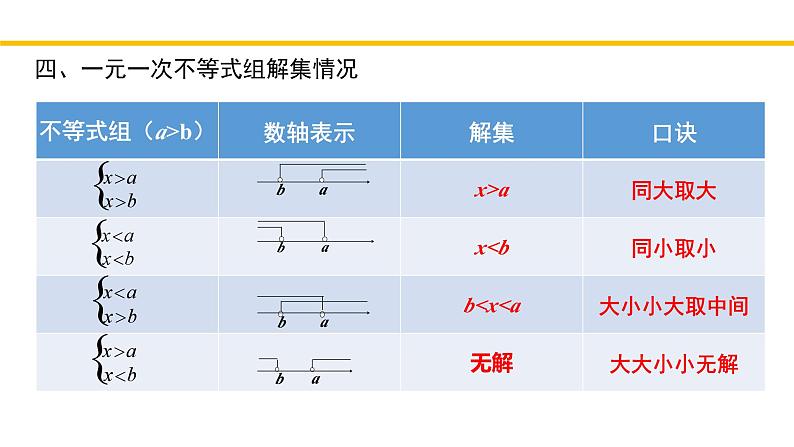
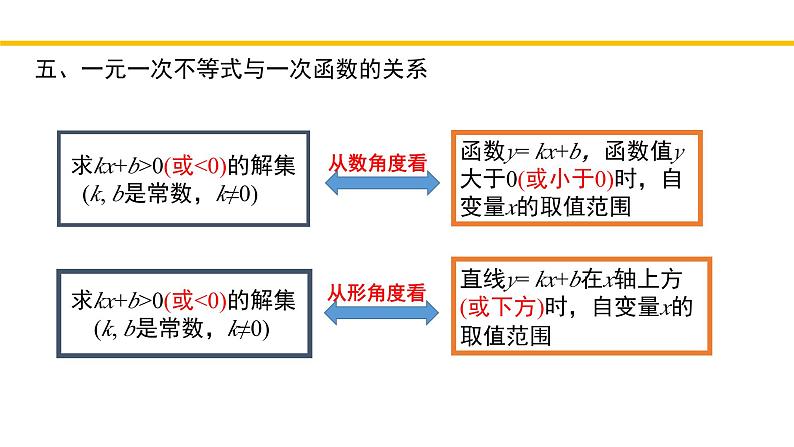
回顾与思考第二章 一元一次不等式与 一元一次不等式组北师大版·八年级下册一、不等式的有关概念用不等号“>”(或“≥”)，“<”(或“≤”)连接的式子叫做不等式.左右两边都是整式，只含有一个未知数，并且未知数的最高次数是1的不等式，叫做一元一次不等式 3x+2 > x–1关于同一未知数的几个一元一次不等式合在一起，就组成一个一元一次不等式组4x+3y<0 一元一次不等式组中各个不等式的解集的公共部分，叫做这个一元一次不等式组的解集.能使不等式成立的未知数的值，叫做不等式的解.一个含有未知数的不等式的所有解，组成这个不等式的解的解集，简称为这个不等式的解集.x=2是不等式x<6的解不等式x+1＞5的解集：x＞4一、不等式的有关概念二、不等式的基本性质不等式的两边都乘（或除以）同一个正数，不等号的方向不变不等式的两边都乘（或除以）同一个负数，不等号的方向改变不等式的两边都加（或减）同一个整式，不等号的方向不变三、解一元一次不等式(组)去分母、去括号、移项、合并同类项、化未知数系数为1，将不等化为xa的形式系数化为1时,不等式的两边都乘或除以同一个负数,这时不等号的方向要改变.(1)求出不等式组中各个不等式的解集；(2)利用数轴或规律，找出这些不等式解集的公共部分；(3)写出了这个不等式组的解集四、一元一次不等式组解集情况五、一元一次不等式与一次函数的关系 求kx+b>0(或<0)的解集 (k, b是常数，k≠0)函数y= kx+b，函数值y大于0(或小于0)时，自变量x的取值范围直线y= kx+b在x轴上方(或下方)时，自变量x的取值范围 求kx+b>0(或<0)的解集 (k, b是常数，k≠0)从数角度看从形角度看六、利用一元一次不等式（组）解决实际问题1.根据题意，适当设出未知数2.找出题中能概括数量间关系的不等关系3.用未知数表示不等关系中的数量4.列出不等式(组)并求出其解集5.检验并根据实际问题的要求写出符合题意的解或解集，并写出答案D 二、考点精讲考点一：不等式(组)的概念例2．下列命题正确的是 （ ）A. 若a>b，bc B. 若a>b，则ac>bcC. 若a>b，则ac2>bc2 D. 若ac2>bc2，则a>bD二、考点精讲考点二：不等式的基本性质B二、考点精讲考点二：不等式的基本性质例4．已知点P（2x+6，x﹣4）在第四象限，则实数x的取值范围在数轴上表示正确的为（　　）A． B． C． D．二、考点精讲考点三：不等式(组)的解集C例5．如果不等式组 的解集是x>3，那么m的取值范围是 ( )A．m≥3　　　　　B．m≤3C．m＝3 D．m<3B二、考点精讲考点三：不等式(组)的解集解：去分母，得 2(2x-1)-(9x+2)≤6， 去括号，得 4x-2-9x-2≤6， 移项，得 4x-9x≤6+2+2， 合并同类项，得 -5x≤10， 系数化1，得 x≥-2. 不等式的解集在数轴上表示如图.二、考点精讲考点四：解一元一次不等式（组）解：解不等式，得 x≤3, 通过观察数轴可知该不等式组的整数解为2,3.二、考点精讲考点四：解一元一次不等式（组）例8． 如图是一次函数y=kx+b的图象，当y＜2时，x的取值范围是 （ ）A．x＜1 B．x＞1 C．x＜3 D．x＞3 C二、考点精讲考点五：一元一次不等式与一次函数关系例9．如图,一次函数y1＝mx+n与y2＝﹣x+a的图象，则0＜mx+n＜﹣x+a的解集为（　　）A．x＞3 B．x＜2 C．2＜x＜3 D．0＜x＜2二、考点精讲考点五：一元一次不等式与一次函数关系C例10．临近期末某班需要购买一些奖品，经过市场考察得知，购买10个钢笔礼盒和1个水杯需要242元，购买1个钢笔礼盒和10个水杯需要341元．（1）你能求出每个钢笔礼盒、每个水杯各多少元？（用二元一次方程组解）（2）根据班级情况，需购进钢笔礼盒和水杯共30个，现要求钢笔礼盒的个数不大于购进水杯的2倍，总费用不超过800元，请你通过计算求出有几种购买方案？哪种方案费用最低？ 二、考点精讲考点六： 不等式(组)的实际应用（2）根据班级情况，需购进钢笔礼盒和水杯共30个，现要求钢笔礼盒的个数不大于购进水杯的2倍，总费用不超过800元，请你通过计算求出有几种购买方案？哪种方案费用最低？二、考点精讲考点六： 不等式(组)的实际应用方案一：当钢笔礼盒15个，则水杯15个时，总费用：15×21+15×32＝795（元）；方案二：当钢笔礼盒16个，则水杯14个时，总费用：16×21+14×32＝784（元）；方案三：当钢笔礼盒17个，则水杯13个时，总费用：17×21+13×32＝773（元）；方案四：当钢笔礼盒18个，则水杯12个时，总费用：18×21+12×32＝762（元）；方案五：当钢笔礼盒19个，则水杯11个时，总费用：19×21+11×32＝751（元）；方案三：当钢笔礼盒20个，则水杯10个时，总费用：20×21+10×32＝740（元）；∴有6种购买方案，购进钢笔礼盒20个，购进水杯10个费用最低． （2）根据班级情况，需购进钢笔礼盒和水杯共30个，现要求钢笔礼盒的个数不大于购进水杯的2倍，总费用不超过800元，请你通过计算求出有几种购买方案？哪种方案费用最低？1．下列不等式中不一定成立的是（　　）A．若x＞y，则﹣x＜﹣y B．若x＞y，则x2＞y2 C．若x＜y，则 ＜ D．若x+m＜y+m，则x＜y三、课堂练习B2. 不等式组 的解集在数轴上表示正确的是（　　） A． B． C． D．B．三、课堂练习2 三、课堂练习4．如图，一次函数y＝kx+b的图象与x轴交于点（4，0），与y轴交于点（0，2），则不等式kx+b＜0的解集为（　　）A．x＜2 B．x＜4 C．x＞2 D．x＞4三、课堂练习B5．如图，在平面直角坐标系中，直线y＝﹣2x和y＝ax+2相交于点A（m，1），则不等式﹣2x＜ax+2的解集为（　　）A．x＜-0.5 B．x＜1 C．x＞1 D．x＞-0.5三、课堂练习D6．如图，已知一次函数y1＝kx＋b(k，b为常数，且k≠0)的图象与x轴交于点A(3，0)，若正比例函数y2＝mx(m为常数，且m≠0)的图象与一次函数的图象相交于点P，且点P的横坐标为1，则关于x的不等式(k－m)x＋b<0的解集为( )A. x<1B．x>1C．x<3D．x>3B三、课堂练习三、课堂练习7．八年级某小组同学去植树，若每人平均植树7棵，则还剩9棵，若每人平均植树9棵，则有1位同学植树的棵数不到2棵．设同学人数为x人，植树的棵数为（7x+9）棵，下列能准确的求出同学人数与种植棵数的不等关系是（　　）A．7x+9≤2+9（x﹣1） B．7x+9≥9（x﹣1） C． D. DC三、课堂练习解：解不等式①得x>－4，解不等式②得x≥－1，所以不等式组的解集 x≥－1.三、课堂练习10.某小区计划购进甲、乙两种树苗，已知甲、乙两种树苗每株分别为8元、6元.若购买甲、乙两种树苗共360株，并且甲树苗的数量不少于乙树苗的一半，请你设计一种费用最少的购买方案.解：设购买甲树苗的数量为x株，依题意得解得 x≥120. ∴购买甲树苗120株，乙树苗240株，此时费用最省.∵甲树苗比乙树苗每株多2元，∴要节省费用，则要尽量少买甲树苗. 又x最小为120， 三、课堂练习11. 某生态体验园推出了甲、乙两种消费卡，设入园次数为x时，所需费用为y元，选择这两种卡消费时，y与x的函数关系如图所示．(1)分别求出选择这两种卡消费时，y关于x的函数表达式；(2)请根据入园次数确定选择哪种卡消费比较合算．解：(1)设y甲＝k1x，根据题意得5k1＝100，解得k1＝20，∴y甲＝20x；设y乙＝k2x＋100，根据题意得：20k2＋100＝300，解得k2＝10，∴y乙＝10x＋100(2)①当y甲y乙时，即20x>10x＋100，解得x>10，当入园次数大于10次时，选择乙消费卡比较合算三、课堂练习课本61页复习题六、布置作业