人教A版 (2019)必修 第二册10.3 频率与概率教学设计

这是一份人教A版 (2019)必修 第二册10.3 频率与概率教学设计，共8页。教案主要包含了教学目标，教学重点，教学难点，孟德尔遗传规律等内容，欢迎下载使用。


教学基本信息
课题
10.3.1频率的稳定性
学科
数学
学段： 高中
年级
高一
教材
书名： 普通高中教科书·数学必修第二册·A版
出版社：人民教育出版社 出版日期： 2019年 6月
教学设计参与人员
姓名
单位
联系方式
设计者
赵燕
北京丰台二中
实施者
赵燕
北京丰台二中
指导者
康舒真
北京教育学院丰台分院
课件制作者
其他参与者
教学目标及教学重点、难点
【教学目标】
（1）了解频率与概率、频率的特性、概率与频率的关系，频率的稳定性等，同时结合实例，会用频率估计概率；
（2）通过观察、比较发现频率的特征（随机性和稳定性），提升直观想象和数据分析素养；
（3）增强基于数据表达现实问题的意识，形成通过数据认识事物的思维品质，积累依托数据探索事物本质、关联和规律的活动经验。
【教学重点】
频率的稳定性
【教学难点】
对频率的稳定性规律的理解
教学过程(表格描述)
教学环节
主要教学活动
设置意图
引入
通过前面的学习，我们知道，对于样本点等可能的试验，可以通过用古典概型公式计算有关事件的概率，例如，抛掷一枚质地均匀的硬币，“正面朝上”的概率为。但是在现实生活中，很多试验的样本点往往不是等可能或者是否等可能不容易判断。例如，抛掷一枚质地不均匀的骰（tu）子，无法判断“正面朝上”和“反面朝上”是否等可能，或者抛掷一枚图钉，无法判断“针尖朝上”和“针尖朝下”是否等可能，在这种情况下就无法通过古典概型公式计算有关事件的概率，需要寻求新的求概率的方法。
引出新课，思考寻求新的求概率的方法
新课
知识回顾
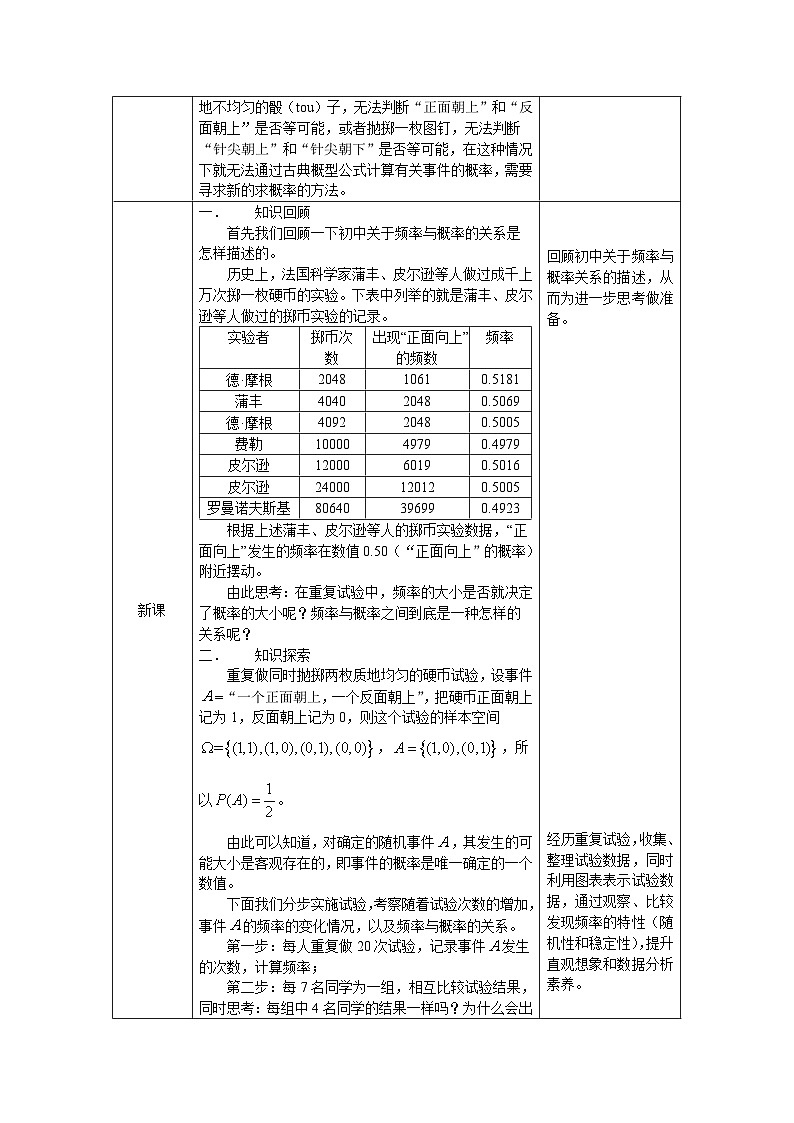
首先我们回顾一下初中关于频率与概率的关系是怎样描述的。
历史上，法国科学家蒲丰、皮尔逊等人做过成千上万次掷一枚硬币的实验。下表中列举的就是蒲丰、皮尔逊等人做过的掷币实验的记录。
实验者
掷币次数
出现“正面向上”的频数
频率
德·摩根
2048
1061
0.5181
蒲丰
4040
2048
0.5069
德·摩根
4092
2048
0.5005
费勒
10000
4979
0.4979
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
罗曼诺夫斯基
80640
39699
0.4923
根据上述蒲丰、皮尔逊等人的掷币实验数据，“正面向上”发生的频率在数值0.50（“正面向上”的概率）附近摆动。
由此思考：在重复试验中，频率的大小是否就决定了概率的大小呢？频率与概率之间到底是一种怎样的关系呢？
知识探索
重复做同时抛掷两枚质地均匀的硬币试验，设事件=“一个正面朝上，一个反面朝上”，把硬币正面朝上记为1，反面朝上记为0，则这个试验的样本空间，，所以。
由此可以知道，对确定的随机事件，其发生的可能大小是客观存在的，即事件的概率是唯一确定的一个数值。
下面我们分步实施试验，考察随着试验次数的增加，事件的频率的变化情况，以及频率与概率的关系。
第一步：每人重复做20次试验，记录事件发生的次数，计算频率；
第二步：每7名同学为一组，相互比较试验结果，同时思考：每组中4名同学的结果一样吗？为什么会出现这样的情况？
第三步：各组统计事件发生的次数，计算事件发生频率，然后汇总数据。
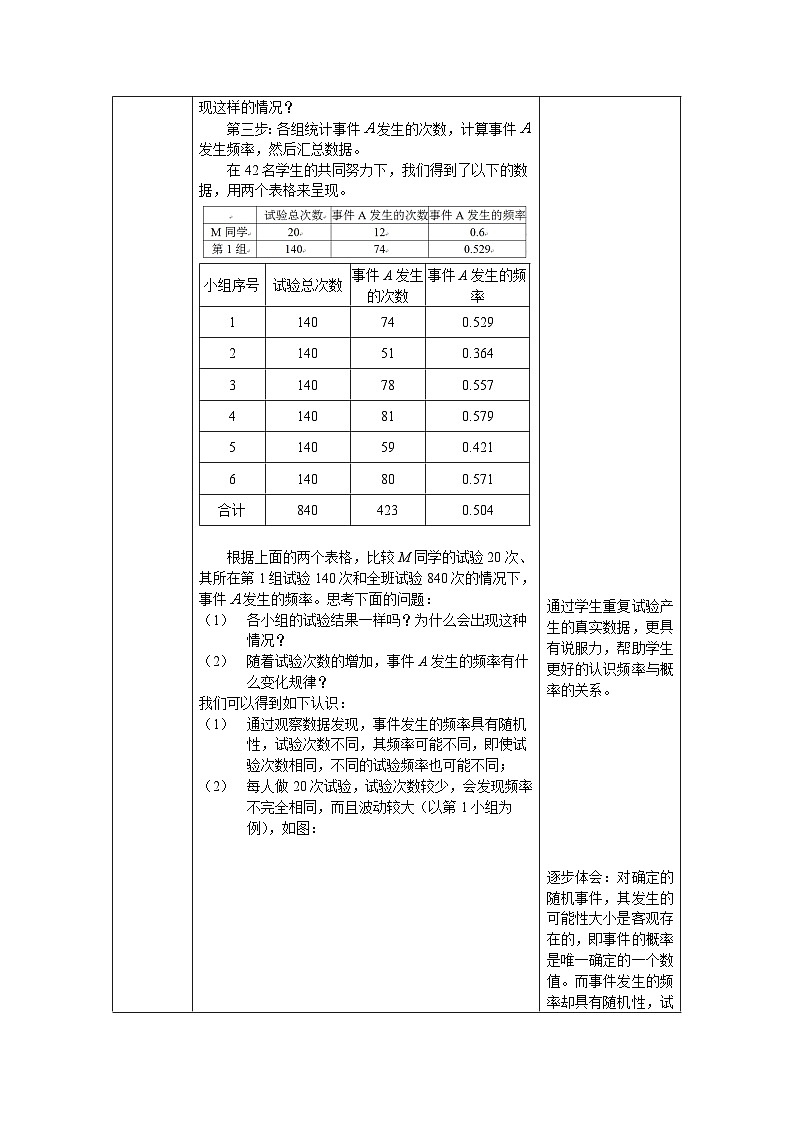
在42名学生的共同努力下，我们得到了以下的数据，用两个表格来呈现。
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
根据上面的两个表格，比较M同学的试验20次、其所在第1组试验140次和全班试验840次的情况下，事件发生的频率。思考下面的问题：
各小组的试验结果一样吗？为什么会出现这种情况？
随着试验次数的增加，事件A发生的频率有什么变化规律？
我们可以得到如下认识：
通过观察数据发现，事件发生的频率具有随机性，试验次数不同，其频率可能不同，即使试验次数相同，不同的试验频率也可能不同；
每人做20次试验，试验次数较少，会发现频率不完全相同，而且波动较大（以第1小组为例），如图：
每个小组做140次试验，再比较各组得到事件A的频率，会发现频率也不完全相同，但是跟第1组比较，波动变小，如图：
汇总42名学生的试验结果，有840次试验会发现频率0.504非常接近事件A的概率0.5。
下面把42位同学试验840次得到的数据0.504与历史上数学家掷币试验所得的数据做对比。
从整体来看，频率在概率0.5附近波动。当试验次数较少时，波动幅度较大；当试验次数较大时，波动幅度较小。但试验次数多的波动幅度并不全都比次数少的小，比如说我们试验840次的频率与0.5的差为0.004，而数学家掷币2048次的频率与0.5的差为0.0181，波动要更大。
随着试验次数的增大，频率偏离概率的幅度会缩小，即事件A发生的频率会逐渐稳定于事件A发生的概率。我们频率的这个性质为频率的稳定性。因此我们用频率估计概率。
【资料】雅各布第一·伯努利（Jakb I Bernulli,1654-1705）瑞士数学家，被公认为概率论的先驱，他给出了著名的大数定律。大数定律阐述了随着试验次数的增加，频率稳定在概率附近。
回顾初中关于频率与概率关系的描述，从而为进一步思考做准备。

经历重复试验，收集、整理试验数据，同时利用图表表示试验数据，通过观察、比较发现频率的特性（随机性和稳定性），提升直观想象和数据分析素养。
通过学生重复试验产生的真实数据，更具有说服力，帮助学生更好的认识频率与概率的关系。
逐步体会：对确定的随机事件，其发生的可能性大小是客观存在的，即事件的概率是唯一确定的一个数值。而事件发生的频率却具有随机性，试验次数不同，其概率的可能不同，即使试验次数相同，不同的试验频率也可能不同。
进一步体会频率与概率的关系，用频率估计概率，比较严格的表述为：“当试验次数较少时，用频率估计概率误差较小的可能性较小；当试验次数足够多时，用频率估计概率误差较小的可能性大”。
对于频率与概率的关系，初中、高中和大学课程中都会出现，学生的认识也是根据自身的思维发展水平逐步加深的，阅读资料中的内容可以推动学生的认识，为将来的学习做准备。
例题
例：新生婴儿性别比是每100名女婴对应的男婴数。通过抽样调查得知，我国2014年，2015年出生的婴儿性别比分别为115.88和113.51.
分别估计我国2014年和2015年男婴的出生率（新生儿中男婴的比率，精确到0.001）；
根据估计结果，你认为“生男孩和生女孩是等可能的”这个判断可靠吗？
第（1）问分析；
首先我们来看性别比是什么意思？根据抽样调查结果，2014年新生儿性别比是115.88，意味着每100名女婴对应的男婴数为115.88，如果样本中2014年新生儿中女婴的频数为100（为某个正实数），那么男婴的频数就应该是115.88（为某个正实数），由此我们可以求出2014年男婴出生的频率。
其次根据频率的稳定性估计男婴的出生率。
下面先给出第（1）问的解答。
假设在抽查的样本中，2014年的女婴数为100（为某个正实数），2015年的女婴数为100（为某个正实数）.
2014年男婴出生的频率为
,
2015年男婴出生的频率为
,
由于调查新生儿人数的样本非常大，根据频率的稳定性，可以估计，我国2014年男婴出生率约为0.537,2015年男婴出生率为0.532.
第（2）问分析：
从决定新生儿性别的生物学理论看，“生男孩和生女孩是等可能的”，平常我们也是接受这样的理论的。这个理论是否绝对正确呢？通过对例题中大量调查数据的分析，来判断“生男孩和生女孩是等可能的”这个理论是否正确。
根据第（1）问的计算结果，可以整理下面的表格：
男婴出生率
女婴出生率
2014年
0.537
0.463
2015年
0.532
0.468
发现生男孩的频率和生女孩的频率有明显的差异，根据频率的稳定性，上述对男婴出生率的估计具有较高的可信度。因此，我们有理由怀疑“生男孩和生女孩是等可能的”的结论。
当然这样的判断还需要经过更客观的假设检验加以确认。
这道例题是根据频率和概率的关系，利用调查数据来判断“生男孩和生女孩是等可能的”的正确性。也就是说对于男婴出生率这样的随机现象，根据生物学知识中有理论概率模型（认为男婴出生率为0.5），然后通过重复试验，用频率进行验证。
反过来，对某个事件，是不是也可以通过大量重复试验发现规律，从而建立概率模型呢？
【孟德尔遗传规律】
奥地利遗传学家孟德尔在1858-1865年的8年间做了大量豌豆杂交试验。他把子叶为黄色和绿色的豌豆杂交，第一年收获的豌豆的子叶都是黄色的；第二年，当他把第一年收获的子叶都是黄色的豌豆再种下时，收获的豌豆的子叶颜色既有黄色也有绿色。同样地，他把圆粒和皱粒豌豆杂交，第一年收获的都是圆粒豌豆；第二年，当他把这种杂交圆粒豌豆再种下时，收获的却既有圆粒豌豆，又有皱粒豌豆。试验的具体数据如下：
豌豆杂交试验的子二代结果
性状
表现1
表现2
表现1：表现2
子叶的颜色
黄色
6022
绿色
2001
3.01:1
种子的形状
圆粒
5474
皱粒
1850
2.96:1
为什么表面完全相同的豌豆会长出这样不同的后代呢？而且每次试验第二年收获的结果比例都接近3:1，非常稳定。孟德尔认为其中一定有某种遗传规律，经过长期的、坚持不懈的研究，孟德尔终于找到了规律，并提出了一种遗传机理的概率模型。这一发现为近代遗传学奠定了基础，孟德尔本人也成为遗传学的奠基人。孟德尔提出的概率模型究竟是怎样的呢？感兴趣的同学可以在课下的时候进一步研究。
【例】
在足球比赛中，若比赛的两只球队均非主场球队，就需要投掷硬币进行开球的优先权，由双方队长各自选择正反面，猜中的队优先开球。你认为这样的开球方式公平吗？
分析：要判断这种方法是否公平，只要看所选取的方法使这两个队选取比赛场地的可能性是否相等即可．因为一枚硬币只有正反两面，所以正面朝上或朝下的概率均为，即两个队选择场地的可能性相等，所以这种方法公平．
总结一下：一个游戏包含两个随机事件A和B，规定事件A发生则甲获胜，事件B发生则乙获胜。判断游戏是否公平的标准是事件A和B发生的概率是否相等。
【问题】在游戏过程中甲发现：玩了10次时，双方各胜5次；但玩到1000次时，自己才胜出300次，而乙却胜了700次。据此，乙认为游戏公平，因为当游戏玩了10次时，甲、乙获胜的频率都为0.5；甲认为游戏不公平，因为当游戏玩到1000次时，甲获胜的频率为0.3，乙获胜的频率为0.7.你更支持谁的结论？为什么？
分析：由于频率的随机性，如果玩的次数较少，难以从双方获胜的频率判断他们获胜的概率是否相等；如果玩的次数足够多，根据频率的稳定性，可以以很大的把握从双方获胜的频率判断他们获胜的概率是否相等。
相对于10次游戏，1000次游戏时的频率接近概率的可能性更大，因此我们更愿意相信1000次游戏的频率离概率更近。而游戏玩到1000次时，甲乙获胜的频率存在较大的差距，所以有理由认为游戏时不公平的，此时支持甲对游戏公平性的判断比支持乙对游戏公平性的判断犯错的可能性要小。因此，应该支持甲对游戏公平性的判断。
本例题是根据频率和概率的关系，利用调查数据来判断“生男孩和生女孩是等可能的”的正确性，也就是利用试验验证概率模型的合理性。
体会通过试验发现规律从而建立概率理论模型的思想。
通过足球比赛赛前掷硬币这一现象，引发对于公平性的思考。
通过甲乙双方胜负的频率来判断“游戏是否公平”，进一步理解频率和概率的关系。
总结
本节课，我们结合具体的随机试验，通过具体的试验来认识频率与概率的关系。概括起来有以下三步：
通过重复试验，探究频率的稳定性规律；
频率与概率的区别与联系；
频率估计概率的应用实例。
频率的稳定性是概率论的理论基础，用频率估计概率是获得随机事件概率的方法之一，也是一种重要的概率思想。
通过小结梳理本节课的主要内容，形成完整的认识。
作业
1.据统计ABO血型具有民族和地区差异。在我国H省调查了30488人，四种血型的人数如下：
血型
A
B
O
AB
人数/人
7704
10765
8970
3049
频率
计算H省各种血型发的频率并填表（精确到0.001）；
如果从H省任意调查一个人的血型，那么他是O型血的概率大约是多少？
2.用掷两枚硬币做胜负游戏，规定：两枚硬币同时出现正面或者同时出现反面算甲胜，一个正面、一个方面算乙胜。这个游戏公平吗？
通过作业巩固本节课知识。