必修 第二册8.1 基本立体图形教案

这是一份必修 第二册8.1 基本立体图形教案，共17页。教案主要包含了【单元目标】，【单元知识结构框架】，【学情分析】，【教学设计思路/过程】，【教学问题诊断分析】，【教学成果自我检测】，【教学反思】等内容，欢迎下载使用。

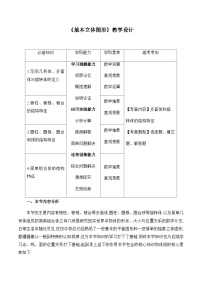
一、【单元目标】
1．知识与技能：
1．通过对实物模型的观察，归纳认知简单多面体——柱、锥、台、球的结构特征．
2．能运用柱、锥、台、球的结构特征来判断、描述现实生活中的实物模型．
3．与平面几何体的有关概念、图形和性质进行适当类比，初步学会用类比的思想分析问题和解决问题．
2．数学学科素养
1.数学抽象：多面体与旋转体等概念的理解；
2.逻辑推理：柱、锥、台、球的结构特点；
3.直观想象：判断空间几何体；
4.数学建模：通过平面展开图将空间问题转化为平面问题解决，体现了转化的思想方法.
二、【单元知识结构框架】
三、【学情分析】
立体几何是研究三维空间中物体的形状、大小、位置关系的一门数学学科，而三维空间是人们生存发展的现实空间，学习立体几何对我们更好地认识客观世界，更好地生存与发展具有重要意义。在立体几何初步部分,学生将先从对空间几何体观察入手、认识空间图形；再以长方体为载体，直观认识和理解空间点、线、面的位置关系。本节内容既是义务教育阶段“空间与图形”课程的延续和提高，也是后续研究空间点、线、面位置关系的基础，既巩固了前面所学的内容，又为后面内容的学习做了知识上和方法上的准备，在教材中起着承前启后的作用。
四、【教学设计思路/过程】
课时安排： 约2课时
第一课时：棱柱、棱锥、棱台的结构特征
第二课时：圆柱、圆锥、圆台、球、简单组合体的结构特征
教学重点：掌握柱、锥、台、球的结构特征；
教学难点：掌握柱、锥、台、球的相关计算.
教学方法/过程：
五、【教学问题诊断分析】
第一课时：棱柱、棱锥、棱台的结构特征
问题1：空间几何体的定义是什么？
【答案】如果只考虑物体的形状和大小，而不考虑其它因素，那么这些由物体抽象出来的空间图形就叫做空间几何体。
【破解方法】在平面几何中，我们认识了三角形，正方形，矩形，菱形，梯形，圆，扇形等平面图形.但我们知道在我们周围存在着各种各样的物体，它们都占据着空间的一部分，利用物体的形状和大小归纳出空间几何体的概念.
问题2：空间几何体分为哪几类？
【答案】空间几何体分为多面体与旋转体，
多面体的定义：由若干平面多边形围成的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面；相邻两个面的公共边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点．
旋转体的定义：由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体．
【破解方法】观察一个物体，将它抽象成空间儿何体，并描述它的结构特征，应先从整体人手，想象围成物体的每个面的形状、面与面之间的关系，并注意利用平面图形的知识.例如像纸箱，金字塔、茶叶盒、金刚石、储物箱等物体有相同的特点:围成它们的每个面都是平面图形，并目都是平面多边形;纸杯、腰鼓、奶粉罐、篮球和足球、铅锤等物体也有相同的特点:围成它们的面不全是平面图形，有些面是曲面.
问题3：常见的多面体有哪些？
【答案】常见的多面体有棱柱、棱锥、棱台.
【破解方法】通过定义及具体例子可以得出常见的多面体的分类。
问题4：棱柱、棱锥、棱台有哪些结构特征？
【答案】棱柱、棱锥、棱台的结构特征
续表
【破解方法】通过定义及具体例子可以得出棱柱、棱锥、棱台的结构特征，提高学生的解决问题、分析问题的能力。
【典型例题】
题型一：棱柱的结构特征
例1．下列关于棱锥、棱台的说法正确的是
A．有两个面平行且相似，其他各面都是梯形的多面体是棱台
B．用一个平面去截棱锥，底面与截面之间部分所围成的几何体叫做棱台
C．棱台的侧面展开图是由若干个等腰梯形组成的
D．棱台的各侧棱延长后必交于一点
【分析】通过棱台的定义判断，；棱台的性质判断，即可．
【解答】解：对于，棱台的各侧棱的延长线交于一点，因此有两个面平行且相似，其他各面都是梯形的多面体不一定是棱台，故错；
对于，用一个平行于底面的平面去截棱锥，底面与截面之间部分所围成的几何体叫做棱台，故错误；
对于，棱台的侧面展开图不一定是由若干个等腰梯形组成的，故错误；
对于，棱台是由平行于棱锥底面的平面截得的，故棱台的各侧棱延长后必交于一点，故正确．
故选：．
【方法总结】
棱柱结构特征的辨析技巧
（1）扣定义：判定一个几何体是否是棱柱的关键是棱柱的定义．
①看“面”，即观察这个多面体是否有两个互相平行的面，其余各面都是四边形；②看“线”，即观察每相邻两个四边形的公共边是否平行．
（2）举反例：通过举反例，如与常见几何体或实物模型、图片等不吻合，给予排除．
题型二：棱锥、棱台的结构特征
例2．下列关于棱柱的说法正确的是
A．所有的棱柱两个底面都平行
B．所有的棱柱一定有两个面互相平行，其余各面都是四边形，每相邻两个四边形的公共边互相平行
C．有两个面互相平行，其余各面都是四边形的几何体一定是棱柱
D．棱柱至少有五个面
【分析】根据棱柱的定义判断．
【解答】解：由棱柱的定义：有两个面互相平行，其余各面都是四边形且相邻四边形的公共边互相平行的几何体是棱柱，知、正确的；
对于，如棱台，有两个面互相平行，其余各个面都是四边形，但它不是棱柱，所以错误；
对于，三棱柱有五个面，楼柱有个面，所以正确，
故选：．
【方法总结】
判断棱锥、棱台形状的两种方法
（1）举反例法
结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确．
（2）直接法
题型三：空间几何体的平面展开图
例3：（1）水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的平面展开图（图中数字写在正方体的外表面上），若图中的“2”在正方体的上面，则这个正方体的下面是（ ）
A．1 B．9
C．快 D．乐
（2）如图是三个几何体的侧面展开图，请问各是什么几何体？
【解】（1）选B.由题意，将正方体的展开图还原成正方体，“1”与“乐”相对，“2”与“9”相对，“0”与“快”相对，所以下面是“9”．
（2）题图①中，有5个平行四边形，而且还有两个全等的五边形，符合棱柱的特点；题图②中，有5个三角形，且具有共同的顶点，还有一个五边形，符合棱锥的特点；题图③中，有3个梯形，且其腰的延长线交于一点，还有两个相似的三角形，符合棱台的特点，把侧面展开图还原为原几何体，如图所示：
所以①为五棱柱，②为五棱锥，③为三棱台．
【方法总结】
多面体展开图问题的解题策略
（1）绘制展开图：绘制多面体的平面展开图要结合多面体的几何特征，发挥空间想象能力或者是亲手制作多面体模型．在解题过程中，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面，便可得到其平面展开图．
（2）由展开图复原几何体：若是给出多面体的平面展开图，来判断是由哪一个多面体展开的，则可把上述过程逆推，同一个几何体的平面展开图可能是不一样的，也就是说，一个多面体可有多个平面展开图．
第二课时 圆柱、圆锥、圆台、球、简单组合体
问题1：旋转体包含哪些图形？
【答案】旋转体包含有圆柱、圆锥、圆台、球.
【破解方法】通过示由平面图形绕着一边进行旋转从而得出各个旋转体，体现从具体到抽象的处理思路.
问题2：圆柱、圆锥、圆台、球是怎样定义的？又有什么结构特点？
【答案】圆柱、圆锥、圆台和球的结构特征
（1）圆柱的结构特征
（2）圆锥的结构特征
（3）圆台的结构特征
（4）球的结构特征
【破解方法】通过定义及实际举例，让学生构建空间感，让学生感受到由平面到空间的变化.
问题3：什么是简单组合体，有几种构成形式？
【答案】（1）概念：由简单几何体组合而成的几何体叫做简单组合体．
（2）两种构成形式：①由简单几何体拼接而成；②由简单几何体截去或挖去一部分而成．
【破解方法】在具体研究方法的指导下，带领学生由整体到局部，去认识空间几何体，对常见简单组合体有深入了解，经历数学抽象的过程，体会刻画几何体结构特征的数学方式。
【典型例题】
题型一：圆柱、圆锥、圆台、球的概念
例1．给出下列说法：
①圆柱的底面是圆面；
②经过圆柱任意两条母线的截面是一个矩形面；
③圆台的任意两条母线的延长线可能相交，也可能不相交；
④夹在圆柱的两个截面间的几何体还是一个旋转体．
其中说法正确的是
A．①②B．①③C．②③D．③④
【分析】根据圆柱的结构特征判断①②是否正确；根据圆台的结构特征判断③错误；举例说明④错误．
【解答】解：对于①，圆柱的底面是两个全等的圆面，所以①正确；
对于②，圆柱的母线都平行且相等，且都垂直于底面，所以经过圆柱任意两条母线的截面是一个矩形面，②正确；
对于③，圆台是由平行于圆锥底面的平面截圆锥得到的，所以圆台的任意两条母线所在的直线都相交，③错误；
对于④，当两个截面不平行或截面平行但不与底面平行时，两个截面间的几何体不是旋转体，所以④错误．
所以正确的命题序号是①②．
故选：．
【归纳总结】
（1）判断简单旋转体结构特征的方法
①明确由哪个平面图形旋转而成；
②明确旋转轴是哪条直线．
（2）简单旋转体的轴截面及其应用
①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量；
②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想．
题型二：简单组合体的结构特征
例2．如图所示的几何体是由下面哪一个平面图形旋转而形成的
A．B．C．D．
【分析】几何体是一个圆柱、两个圆台和一个圆锥的组合体，由此能求出结果．
【解答】解：几何体是一个圆柱、两个圆台和一个圆锥的组合体，
它是由选项中的平面图形旋转而成的．
故选：．
【归纳总结】
不规则平面图形旋转形成几何体的结构特征的分析策略
（1）分割：首先要对原平面图形适当分割，一般分割成矩形、梯形、三角形或圆（半圆或四分之一圆）等基本图形．
（2）定形：然后结合圆柱、圆锥、圆台、球的形成过程进行分析．
题型三：旋转体中的计算问题
例3．已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为 ．
【分析】根据圆锥的侧面展开图为一个半圆，底面圆的周长等于半圆的弧长，由此求出圆锥的母线长．
【解答】解：圆锥的底面半径为，其侧面展开图为一个半圆，
所以，
解得，
所以该圆锥的母线长为．
故答案为：．
【归纳总结】
解决旋转体中计算问题的方法
用平行于底面的平面去截柱、锥、台等几何体，注意抓住截面的性质（与底面全等或相似），同时结合旋转体中的轴截面（经过旋转轴的截面）的几何性质，利用相似三角形中的相似比，列出相关几何变量的方程（组）而解得．
在研究与截面有关的问题时，要注意截面与物体的相对位置的变化．由于相对位置的改变，截面的形状也会随之发生变化．
六、【教学成果自我检测】
1．课前预习
设计意图：落实与理解教材要求的基本教学内容.
1．如图所示，观察四个几何体，其中判断正确的是
A．（1）是棱台B．（2）是圆台C．（3）是棱锥D．（4）不是棱柱
【分析】利用几何体的结构特征进行分析判断，能够求出结果．
【解答】解：图（1）不是由棱锥截来的，所以（1）不是棱台；
图（2）上、下两个面不平行，所以（2）不是圆台；
图（3）是棱锥．
图（4）前、后两个面平行，其他面是平行四边形，且每相邻两个四边形的公共边平行，所以（4）是棱柱．
故选：．
2．将选项中所示的三角形绕直线旋转一周，可以得到如图所示的几何体的是
A．B．
C．D．
【分析】几何体的是有相同底面的两个圆锥的组合体，应该是钝角三角形绕直线旋转一周而成．
【解答】解：如图所示的几何体的是有相同底面的两个圆锥的组合体，
应该是钝角三角形绕直线旋转一周，
结合选项中所示的三角形，
应该是中三角形绕直线旋转一周，图示的几何体．
故选：．
3．下列结论中正确的是
A．半圆弧以其直径为轴旋转一周所形成的曲面叫做球
B．直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥
C．夹在圆柱的两个平行截面间的几何体还是一个旋转体
D．用一个平面截圆锥底面与截面组成的部分是圆台
【分析】根据题意，分析选项中的命题，判断命题是否正确即可．
【解答】解：对于，因为半圆弧以其直径为轴旋转一周所成的曲面叫做球面，
球面围成的几何体叫做球体，所以错误；
对于，当以直角三角形的直角边所在直线为轴旋转时，
其余各边旋转形成的面所围成的几何体是圆锥，所以正确；
对于，当两个平行截面不平行于上、下两个底面时，
两个平行截面间的几何体不是旋转体，所以错误；
对于，圆锥的截面不与底面平行时，
圆锥底面与截面组成的部分不是圆台，所以错误．
故选：．
4．如图所示，下列四个几何体：
其中不是棱柱的序号是
A．①B．②C．③D．④
【分析】利用棱柱的定义，判断几何体的正误即可．
【解答】解：根据棱柱的定义，有两个面互相平行，其余各面都是四边形，
并且每相邻两个四边形的公共边都互相平行，
由这些面所围成的多面体，可知
①是三棱柱；②是多面体，不是棱柱；③是四棱柱；④是四棱柱．
故选：．
2．课堂检测
设计意图：例题变式练.
【变式1】下列说法错误的是
A．长方体有6个面
B．三棱锥有4个顶点
C．三棱台有9条棱
D．三棱柱的侧面是全等的平行四边形
【分析】根据几何体的结构特征进行分析，判断面、棱、顶点个数．
【解答】解：长方体属于四棱柱，故长方体有4个侧面，2个底面，故正确；
三棱锥底面为三角形，底面有3个顶点，三棱锥的3个侧面还有1个公共顶点，
故三棱锥有4个顶点，故正确；
三棱台上底面有3条棱，下底面有3条棱，还有3条侧棱，故三棱台有9条棱，故正确；
三棱柱的底面边长不一定相等，故三棱柱的侧面不一定全等，故错误．
故选：．
【变式2】如图所示的组合体，其结构特征是
A．由两个圆锥组合成的
B．由两个圆柱组合成的
C．由一个棱锥和一个棱柱组合成的
D．由一个圆锥和一个圆柱组合成的
【分析】由图形知该几何体是上边为圆锥体，下边为圆柱体的组合体．
【解答】解：由图形知，该几何体由一个圆锥和一个圆柱组成的简单组合体．
故选：．
【变式3】下面关于空间几何体叙述不正确的是
A．底面是正多边形的棱锥是正棱锥
B．棱柱的侧面都是平行四边形
C．直平行六面体是长方体
D．直角三角形以其一边所在直线为轴旋转一周形成的几何体是圆锥
【分析】对于，顶点在底面的射影是底面正多边形的中心，即可判断；
对于，由棱柱的性质可判断；
对于，由侧棱与底面不垂直进行判断；
对于，直角三角形以其一直角边所在直线为旋转轴旋转一周形成的曲面所围成的几何体是圆锥，由此即可判断．
【解答】解：对于，底面是正多边形，顶点在底面的射影是底面正多边形的中心的棱锥是正棱锥，故错误；
对于，由棱柱的性质可得棱柱的侧面都是平行四边形，故正确；
对于，直平行六面体是平行六面体的侧棱与底面垂直，底面可以是平行四边形，它不是长方体，故错误；
对于，直角三角形以其一直角边所在直线为旋转轴旋转一周形成的曲面所围成的几何体是圆锥，故错误．
故选：．
【变式4】下列命题中错误的是
A．有两个面平行，其余各面都是四边形的几何体叫棱柱
B．有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
C．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台
D．有两个面平行，其余各面都是平行四边形的几何体叫棱柱
【分析】直接利用棱柱的定义，棱台的定义判断、、、的结论．
【解答】解：对于：如图所示：
有两个面平行，其余各面都是四边形的几何体，
例如两个倒扣的棱柱满足该条件，但是不叫棱柱，故错误；
对于：有两个面平行，其余各面都是四边形，
并且每相邻两个四边形的公共边都互相平行的几何体，满足棱柱的定义，叫棱柱，故正确；
对于：用一个平行于底面的平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台，故错误；
对于：有两个面平行，其余各面都是平行四边形的几何体，
例如两个倒扣的棱柱满足该条件，图形和一样，但是不叫棱柱，故错误；
故选：．
【变式5】如图所示，用一个平行于圆锥底面的平面截这个圆锥，截得的圆台上、下底面的面积之比为，截去的圆锥的底面半径是，圆锥的高为．
（1）求圆台的母线长；
（2）若该棱锥中有一内接正方体，试求正方体的棱长．
【分析】（1）设圆台的母线长为，由截得的圆台上、下底面面积之比为，得到，进而利用勾股定理求解即可；
（2）过正方体的体对角线作圆锥的轴截面，设正方体的棱长为，得到，求解即可．
【解答】解：（1）设圆台的母线长为，由截得的圆台上、下底面面积之比为，
可设截得圆台的上、下底面的半径分别为，，过轴作截面，如图所示，
则△，，
，，
，．
又，
，，
，即圆台的母线长为．
（2）如图，过正方体的体对角线作圆锥的轴截面，设正方体的棱长为，
则，
因为，即，
解得，
故正方体的棱长为．
3．课后作业
设计意图：巩固提升.
1.课本104页练习
2.课本习题8.1复习巩固及综合运用
七、【教学反思】
结构特征及分类
图形及记法
棱柱
结构特征
（1）有两个面（底面）互相平行
（2）其余各面都是四边形
（3）相邻两个四边形的公共边都互相平行
记作棱柱
ABCDEF­A′B′C′D′E′F′
分类
按底面多边形的边数分为三棱柱、四棱柱…
结构特征及分类
图形及记法
棱锥
结构特征
（1）有一个面（底面）是多边形
（2）其余各面（侧面）都是有一个公共顶点的三角形
记作
棱锥S­ABCD
分类
按底面多边形的边数分为三棱锥、四棱锥……
棱台
结构特征
（1）上下底面互相平行，且是相似图形
（2）各侧棱延长线相交于一点
（或用一个平行于棱锥底面的平面去截棱锥，底面与截面之间那部分多面体叫做棱台）
记作
棱台ABCD­A′B′C′D′
分类
由三棱锥、四棱锥、五棱锥……截得的棱台分别为三棱台、四棱台、五棱台……
棱锥
棱台
定底面
只有一个面是多边形，此面即为底面
两个互相平行的面，即为底面
看侧棱
相交于一点
延长后相交于一点
定义
以矩形的一边所在直线为旋转轴，其余三边旋转一周形成的面所围成的旋转体
图示及相关概念
轴：旋转轴叫做圆柱的轴
底面：垂直于轴的边旋转而成的圆面
侧面：平行于轴的边旋转而成的曲面
母线：无论旋转到什么位置，平行于轴的边
柱体：圆柱和棱柱统称为柱体
定义
以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体
图示及相关概念
轴：旋转轴叫做圆锥的轴
底面：垂直于轴的边旋转而成的圆面
侧面：直角三角形的斜边旋转而成的曲面
母线：无论旋转到什么位置，不垂直于轴的边
锥体：圆锥和棱锥统称为锥体
定义
用平行于圆锥底面的平面去截圆锥，底面与截面之间的部分
图示及相关概念
轴：圆锥的轴
底面：圆锥的底面和截面
侧面：圆锥的侧面在底面和截面之间的部分
母线：圆锥的母线在底面与截面之间的部分
台体：圆台和棱台统称为台体
定义
以半圆的直径所在直线为旋转轴，旋转一周形成的曲面叫做球面，球面所围成的旋转体叫做球体，简称球
图示及相关概念
球心：半圆的圆心
半径：半圆的半径
直径：半圆的直径