人教A版 (2019)必修 第二册8.2 立体图形的直观图教案

这是一份人教A版 (2019)必修 第二册8.2 立体图形的直观图教案，共7页。教案主要包含了【单元目标】，【单元知识结构框架】，【学情分析】，【教学设计思路/过程】，【教学问题诊断分析】，【教学成果自我检测】等内容，欢迎下载使用。
一、【单元目标】
1．知识与技能：
（1）了解“斜二测画法”的概念并掌握斜二测画法的步骤．
（2）会用斜二测画法画出一些简单平面图形和立体图形的直观图．
2．过程与方法：
通过类比,利用斜二测画法画出平面图形和空间几何体的直观图.
3．情感态度与价值观：
（1）提高空间想象能力与直观感受
（2）体会类比在学习中的作用.
（3）感受几何作图在生产生活中的作用.
（4）通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。
二、【单元知识结构框架】
三、【学情分析】
1．认知基础
本节课选自《普通高中课程标准数学教科书-必修第二册》（人教A版）第八章《立体几何初步》，本节课主要平面图形、空间几何体的直观图的画法。
画出空间几何体的直观图是学生学好立体几何的必要条件。本节课主要是介绍了最常用的、直观性好的斜二测画法。而水平放置的平面图形的直观图画法,是画空间几何体直观图的基础。教学的重点是斜投影画平面图形直观图的方法,即斜二测画法。教材给出了正六边形、长方体、圆柱、圆柱和圆锥组合体直观图的画法。教学时可以适当延伸,讨论正五边形、圆锥、圆台、球的直观图画法。
画空间几何体的直观图，了解空间几何体的直观图，有助于提高学生的空间想象能力，是学生学习点、直线、平面之间位置关系的基础。
2.认知障碍
一方面，学生对于立体空间感没有建立，需要在老师的启发引导下探究体会由平面图形到立体图形的转换；另一方面，让学生体会横不变纵减半画图可以得出最佳立体感，培养学生的作图能力和直观想象能力.
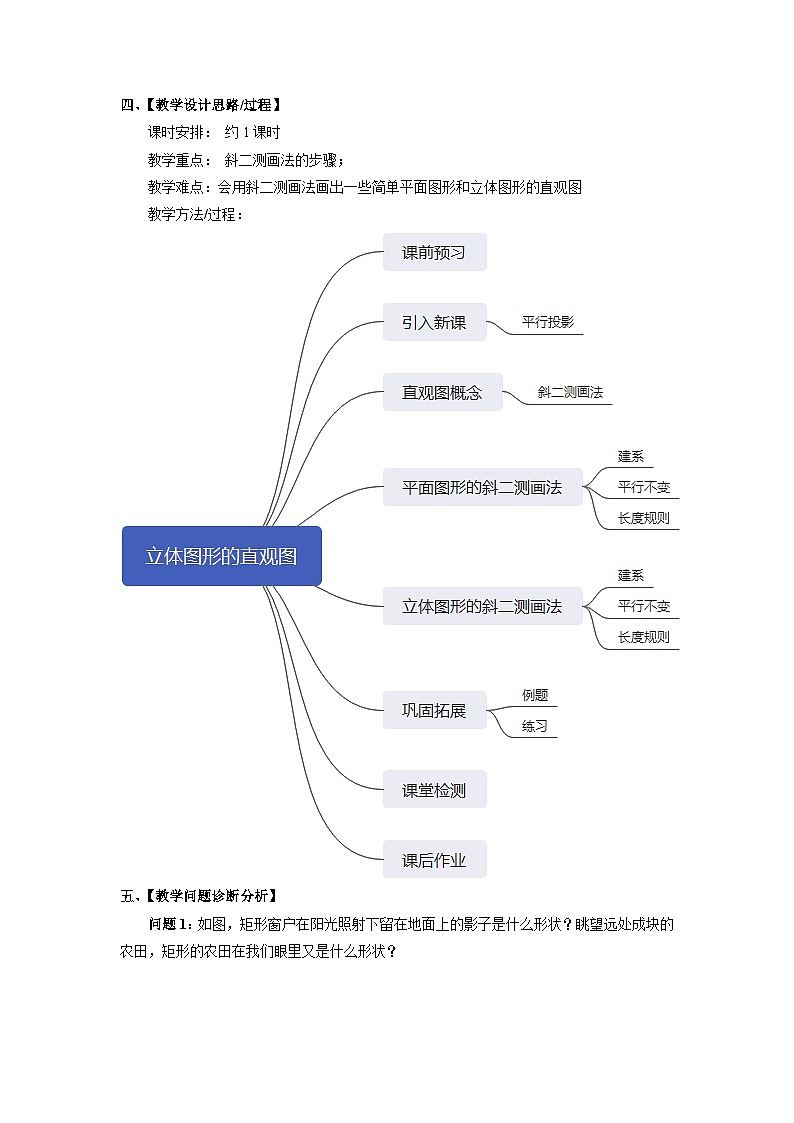
四、【教学设计思路/过程】
课时安排： 约1课时
教学重点： 斜二测画法的步骤；
教学难点：会用斜二测画法画出一些简单平面图形和立体图形的直观图
教学方法/过程：
五、【教学问题诊断分析】
问题1：如图，矩形窗户在阳光照射下留在地面上的影子是什么形状？眺望远处成块的农田，矩形的农田在我们眼里又是什么形状？
【答案】平行四边形
【破解方法】通过学生熟悉的身边环境，引发学生思考，让学生了解平面图形的的直观图，提高学生的解决问题、分析问题的能力。
问题2：利用平行投影，获得的画直观图的方法是什么？
【答案】斜二测画法
【破解方法】通过了解概念，从平行投影到平面图形的直观图的画法，根据总结得出最能体现出立体感的作图方法，即斜二测画法.
问题3：用斜二测画法画水平放置的平面图形的直观图的步骤是怎样的？
【破解方法】通过斜二测画法的讲解，让学生了解到斜二测画法作平面图形的关键：①建系；②平行关系；③长度规则.
【教学过程】用斜二测画法画水平放置的平面图形的直观图的步骤：
(1)在已知图形中取互相垂直的x轴和y轴，两轴相交于点O画直观图时，把它们画成对应的轴与轴，两轴相交于点 ，使(或 )，它们确定的平而表示水平面.
(2)已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于轴与轴的线段.
(3)已知图形中平行于x轴的线段。在直观图中保持原长度不变，平行于y轴的线段，在直观图中长度为原来的一半.
问题4：具体怎么用斜二测画法画水平放置的正方形的直观图？
【破解方法】通过讲解步骤，让学生了解注意画平面图形的直观图，提高学生分析问题、概括能力。
【教学过程】①以正方形的中心为原点，平行与边的直线为x轴，y轴建立如图所示的坐标系；
②建立=45°的坐标系
③平行于x、y轴的线段在斜二测坐标系中仍平行于轴与轴，但横向长度不变，纵向长度减半
问题5：用斜二测画法画空间几何体的直观图的步骤是什么？
【破解方法】和利用斜二测画平面图形的方法的对比，理解利用斜二测画法画空间几何体的直观图的步骤的异同，通过后面具体例题进一步巩固空间几何体直观图的画法，提高学生画图的能力、直观想象能力.
【教学过程】画几何体的直观图时，与画平面图形的直观图相比，只是多画一个与x轴、y轴都垂直的z轴，并且使平行于z轴的线段的平行性和长度都不变.
问题6：能具体说说怎么利用斜二测画法作已知长方体的长,宽,高分别是3cm,2cm,1.5cm的直观图吗？
【破解方法】通过具体例题进一步巩固利用斜二测画法作立体图形的直观图的步骤提高学生画图的能力、直观想象能力，与画平面图形的直观图相比，只是多画一个与x轴、y轴都垂直的z轴，作直观图是必须利用几个平行关系进行定位，充分理解长度的变与不变的应用.
【教学过程】画法：（1）画轴。画三轴交于点O，使。
画底面。在x轴正半轴上取线段AB，使AB=3cm，在y轴正半轴上取线段AD，使AD=1cm,过点B作y轴的平行线，过点D作x轴的平行线，设它们的交点为C,则平行四边形ABCD就是长方体的底面ABCD的直观图。
（3）画侧棱。在z轴正半轴上取线段，使，过B，C，D各点分别作z轴的平行线，并在这些平行线上分别截取1.5cm长的线段
（4）成图。顺次连接，并加以整理（去掉辅助线，将被遮挡部分改成虚线），就可得到长方体的直观图。
六、【教学成果自我检测】
1．课前预习
设计意图：落实与理解教材要求的基本教学内容.
用斜二测画法画水平放置的平面图形的直观图时，下列结论是否正确。
(1) 相等的线段在直观图中仍然相等。 （ ）
(2) 平行的线段在直观图中仍然平行。 （ ）
(3)一个角的直观图仍然是一个角。 （ ）
(4) 相等的角在直观图中仍然相等。 （ ）
【答案】（1）× （2）√ （3） √ （4） ×
【解析】对于（1）；利用斜二测画法横不变纵减半，所以相等的线段在直观图中不一定相等，（1）是假命题；
对于（2）；利用斜二测画法，平行的线段在直观图中仍然平行；所以，（2）是真命题；
对于（3）；利用斜二测画法，一个角的直观图仍然是一个角，是真命题；
对于（4）；因为直观图中横不变纵减半，则相等的角在直观图中不一定相等，所以，（4）是假命题；
2、用斜二测画法画水平放置的六边形的直观图
【解析】（1）在六边形ABCDEF中，取AD所在的直线为x轴，对称轴MN所在直线为y轴，两轴交于点O。画相应的轴和轴，两轴相交于点，使
（2）以为中心，在轴上取，在轴上 取，以点为中心，画平行与轴，并且等于BC；再以为中心，画平行于轴，并且等于EF。
（3）连接 ，并擦去辅助线轴和轴，便获正六边形ABCDEF水平放置的直观图 。
3、如图，平行四边形O′P′Q′R′是四边形OPQR的直观图，若O′P′＝3，O′R′＝1，则原四边形OPQR的周长为 ．
【答案】10
【解析】由直观图可知，原图形是矩形OPQR，且OP＝3，OR＝2.故原四边形OPQR的周长为10.
4．画出水平放置的四边形OBCD(如图所示)的直观图．
【解析】 (1)过点C作CE⊥x轴，垂足为点E，如图①所示，画出对应的x′轴、y′轴，使∠x′O′y′＝45°，如图②所示．
① ② ③
(2)如图②所示，在x′轴上取点B′，E′，使得O′B′＝OB，O′E′＝OE；在y′轴上取一点D′，使得O′D′＝eq \f(1,2)OD；过点E′作E′C′∥y′轴，使E′C′＝eq \f(1,2)EC.
(3)连接B′C′，C′D′，并擦去x′轴与y′轴及其他一些辅助线，如图③所示，
四边形O′B′C′D′就是所求的直观图．
2．课堂检测
设计意图：例题变式练.
【变式1】判断正误
用斜二测画法画水平放置的平面图形的直观图.
(1)原来相交的仍相交.( )
(2)原来垂直的仍垂直.( )
(3)原来平行的仍平行.( )
(4)原来共点的仍共点.( )
【答案】 (1)√ (2)× (3)√ (4)√
【解析】(1) 正确；利用斜二测画法，平行的仍然平行，原来相交的仍相交；
(2) 错；长度有可能改变，故垂直关系改变；
(3) 正确；利用斜二测画法，平行的仍然平行，原来相交的仍相交；
(4) 正确；利用斜二测画法，平行的仍然平行，原来相交的仍相交；
(6) 正确；规定:零向量与任意向量平行.
【变式2】利用斜二测画法画出边长为3 cm的正方形的直观图，正确的是( )
A B C D
【答案】C
【解析】正方形的直观图应是一个内角为45°的平行四边形，且相邻的两边之比为2∶1，故选C.
3．课后作业
设计意图：巩固提升.
1.课本109页练习
2.课本习题8.2复习巩固及综合运用