高中数学人教A版 (2019)选择性必修 第三册7.1 条件概率与全概率公式学案
展开1.通过实例,了解条件概率的概念;
2.掌握求条件概率的两种方法;
3.能利用条件概率公式解决一些简单的实际问题;
4.通过条件概率的形成过程,体会由特殊到一般的思维方法.
重点:运用条件概率的公式解决简单的问题
难点:条件概率的概念
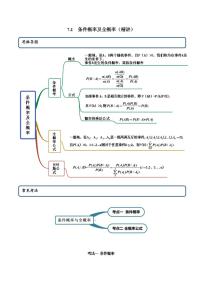
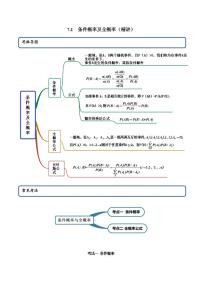
1.条件概率
一般地,当事件B发生的概率大于0时(即P(B)>0),已知事件B发生的条件下事件A发生的概率,称为条件概率,记作P(A|B), 而且P(A|B)=P(A⋂B)P(B).
2. 概率的乘法公式
由条件概率的定义,对任意两个事件A与B,若P(A)>0,则
P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式(multiplicatin frmula).
3.条件概率的性质
条件概率只是缩小了样本空间,因此条件概率同样具有概率的性质.
设P(A)>0,则
(1)P(Ω|A)=1;
(2)如果B和C是两个互斥事件,则P(BUC |A)=P(B | A)+P(C | A);
(3)设B和B互为对立事件,则P( B |A)=1- P(B|A).
问题探究
在必修“概率” 一章的学习中,我们遇到过求同一实验中两个事件A与B同时发生(积事件AB)的概率的问题,当事件A与B相互独立时,有
P(AB)=P(A)P(B)
如果事件A与B不独立,如何表示积事件AB的概率呢?下面我们从具体问题入手.
问题1 . 某个班级有45名学生,其中男生、女生的人数及团员的人数如表所示,
在班级里随机选一人做代表,
(1)选到男生的概率是多大?
(2)如果已知选到的是团员,那么选到的是男生的概率是多大?
问题2. 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭,随机选一个家庭,那么
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
分析:求P(B|A)的一般思想
AB
A
B
因为已经知道事件A 必然发生,所以只需在A 发生的范围内考虑问题,即现在的
样本空间为A.
因为在事件A发生的情况下事件B 发生,等价于事件A 和事件 B 同时发生,
即AB发生.所以事件A 发生的条件下,事件B 发生的概率P(B|A) = n(AB)n(A).
为了把这个式子推广到一般情形,不妨记原来的样本空间为W,则有
P(B|A) = n(AB)n(W)n(A)n(W)=P(AB)P(A).
一般地,当事件B发生的概率大于0时(即P(B)>0),已知事件B发生的条件下事件A发生的概率,称为条件概率,记作P(B|A), 而且P(B|A)=P(AB)P(A).
问题1. 如何判断条件概率?
问题2. P(B|A)与P(A|B)的区别是什么?
条件概率与事件独立性的关系
探究1:在问题1和问题2中,都有P(B|A)≠P(B).一般地, P(B|A)与P(B)不一定相等。如果P(B|A)与P(B)相等,那么事件A与B应满足什么条件?
探究2:对于任意两个事件A与B,如果已知P(A)与P(B|A),如何计算P(AB)呢?
二、典例解析
例1.在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例2:已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗?
例3: 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率。
跟踪训练1.一个盒子中有6只好晶体管,4只坏晶体管,任取两次,每次取一只,每一次取后不放回.若已知第一只是好的,求第二只也是好的的概率.
1.已知P(AB)=12,P(A)=35,则P(B|A)等于( )
A.56B.910 C.310D.110
2.下列说法正确的是( )
A.P(A|B)=P(B|A) B.P(B|A)>1
C.P(A∩B)=P(A)·P(B|A) D.P((A∩B)|A)=P(B)
3.设A,B为两个事件,若事件A和B同时发生的概率为310,在事件A发生的条件下,事件B发生的概率为12,则事件A发生的概率为 .
4.某气象台统计,该地区下雨的概率为415,刮四级以上风的概率为215,既刮四级以上的风又下雨的概率为110.设A为下雨,B为刮四级以上的风,求P(B|A).
5.在100件产品中,有95件合格品,5件不合格品,现从中不放回地取两次,每次任取1件产品.试求:
(1)第一次取到不合格品的概率;
(2)在第一次取到不合格品后,第二次再次取到不合格品的概率.
6.在某次考试中,要从20道题中随机地抽出6道题,若考生至少答对其中的4道题即可通过;若至少答对其中5道题就获得优秀.已知某考生能答对其中10道题,并且知道他在这次考试中已经通过,求他获得优秀成绩的概率.
参考答案:
知识梳理
学习过程
问题探究
问题1 .随机选择一人作代表,则样本空间?包含45个等可能的样本点.用A表示事件“选到团员”, B表示事件“选到男生” ,根据表中的数据可以得出n(Ω)=45, n(A)=30, n(B)=25.
(1)根据古典概型知识可知选到男生的概率
P(B) = n(B)n(Ω)=2545=59.
(2)“在选择团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生” 的概率,记为P(B|A).此时相当以A为样本空间来考虑B发生概率,而在新的样本空间中事件B就是积事件AB,包含了样本点数nAB=16.根据古典概型知识可知:P(B|A) = n(AB)n(A)=1630=815.
问题2.观察两个小孩的性别,用b表示男孩,g表示女孩,则样本空间Ω=bb,bg,bg,gg,且所有样本点是等可能的.用A表示事件“选择家庭中有女孩” ,B表示事件“选择家庭中两个孩子都是女孩” ,A =bg,gb,gg, B=gg.
(1) 根据古典概型知识可知,该家庭中两个小孩都是女孩的概率
P(B) = n(B)n(Ω)=14.
(2)“在选择的家庭有女孩的条件下,两个小孩都是女孩” 的概率就是在“事件A发生的条件下,事件B发生” 的概率,记为P(B|A) ,此时A成为样本空间,事件B就是积事件AB,根据古典概型知识可知
P(B|A) = n(AB)n(A)=13.
问题1. 题目中出现“在已知……前提下(或条件下)”“在A发生的条件下”等关键词,表明这个前提已成立或条件已发生,此时通常涉及条件概率.
问题2. P(B|A)表示在事件A发生的条件下,B发生的概率.
P(A|B)表示在事件B发生的条件下,A发生的概率.
条件概率与事件独立性的关系
探究1: 直观上看,当事件A与B相互独立时,事件A发生与否不影响事件B发生的概率,
这等价于P(B|A)=P(B)成立.
事实上,若事件A与B相互独立,即PAB=PAPB,且PA>0,则
PBA=P(AB)PA=PAPBPA=PB;
反之,若PBA=PB,且PA>0,则
PB=PABPA ⇒ PAB=PAPB
探究2:由条件概率的定义,对任意两个事件A与B,若P(A)>0,则
P(AB)=P(A)P(B|A).
我们称上式为概率的乘法公式(multiplicatin frmula).
二、典例解析
例1.分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率.可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”。
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB.从5道试题中每次不放回地随机抽取2道,试验的样本空间Ω包含20个等可能的样本点,即nΩ=A52=5×4=20。
因为n(AB)= A31×A21=3×2=6
P(AB) = n(AB)n(Ω)=620=310.
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率。显然P(A)=35.利用条件概率公式,得
P(B|A) = n(AB)n(A)=31035=12.
解法2:在缩小的样本空间A上求P(B|A).已知第1次抽到代数题,这时
还余下4道试题,其中代数题和几何题各2道.因此,事件A发生的条件下,
事件B发生的概率为
P(B|A)=12.
又P(A)= 35 ,利用乘法公式可得
P(AB)=P(A) P(B|A)= 35 ×12= 310.
从例1可知,求条件概率有两种方法:
方法一:基于样本空间Ω,先计算P(A)和P(AB),再利用条件概率公式求
P(B|A);
方法二:根据条件概率的直观意义,增加了“A发生”的条件后,样本空间缩小为A,求P(B|A)就是以A为样本空间计算AB的概率。
例2:解:用A,B,C分别表示甲、乙、丙中奖的事件,则B=AB,C=AB.PA=13;
PB=PAB=PAPB|A=23×12=13
PC=PAB=PAPB|A=23×12=13
因为P(A)= P(B)= P(C),所以中奖的概率与抽奖的次序无关。
例3: 解:(1)设Ai=“第i次按对密码”(i=1,2),则事件“不超过2次就按对密码”可表示为A=A1UA1A2.
事件A1与事件A1A2互斥,由概率的加法公式及乘法公式,得
P(A)=P(A1)+P( A1A2 )= P(A1) +P (A1 ) P( A2 | A1 ) =110+910× 19= 15
因此,任意按最后1位数字,不超过2次就按对的概率为15.
(2)设B=“最后1位密码为偶数”,则
P(A|B)=P(A1|B)+P(A1A2|B)=15+4×15×4= 25;
因此,如果记得密码的最后1位是偶数,不超过2次就按对的概率为25.
跟踪训练1.解:方法一(定义法)
设Ai={第i只是好的}(i=1,2).由题意知要求出P(A2|A1).因为P(A1)=610=35,P(A1A2)=6×510×9=13,
所以P(A2|A1)=P(A1A2)P(A1)=59.
方法二(直接法)
因为事件A1已发生(已知),故我们只研究事件A2发生便可,在A1发生的条件下,盒中仅剩9只晶体管,其中5只好的,即n(AB)=5,n(A)=9,所以P(A2|A1)=n(AB)n(A)=59.
达标检测
1.解析:P(B|A)=P(AB)P(A)=1235=56.
答案:A
2.解析:由P(B|A)=P(A⋂B)P(A)知,P(A∩B)=P(A)·P(B|A).
答案:C
3.解析:由题意知,P(A∩B)=310,P(B|A)=12.
由P(B|A)=P(A⋂B)P(A),得P(A)=P(A⋂B)P(B|A)=35.
答案:35
4.解:由题意知P(A)=415,P(A∩B)=110,
故P(B|A)=P(A⋂B)P(A)=110415=38.
5.分析:由题意可知,100件产品中共有5件不合格品,不合格率为 5100.在第一次取到不合格品的条件下,第二次又取到不合格品的概率为条件概率.
解:设第一次取到不合格品为事件A,第二次取到不合格品为事件B,则有:
(1)P(A)=5100=0.05.
(2)方法一:第一次取到一件不合格品,还剩下99件产品,其中有4件不合格品,95件合格品,于是第二次又取到不合格品的概率为499,由于这是一个条件概率,
所以P(B|A)=499.
方法二:根据条件概率的定义,先求出事件A,B同时发生的概率P(AB)=C52C1002=1495,
所以P(B|A)=P(AB)P(A)=14955100=499.
6.解:设事件A为“该考生6道题全答对”,事件B为“该考生答对了其中5道题而另一道答错”,事件C为“该考生答对了其中4道题而另2道题答错”,事件D为“该考生在这次考试中通过”,事件E为“该考生在这次考试中获得优秀”,则A,B,C两两互斥,且D=A∪B∪C,E=A∪B,由古典概型的概率公式及加法公式可知P(D)=P(A∪B∪C)=P(A)+P(B)+P(C)
=C106C206+C105C101C206+C104C102C206=12 180C206,P(E|D)=P(A∪B|D)=P(A|D)+P(B|D)
=P(A)P(D)+P(B)P(D)=210C20612 180C206+2 520C20612 180C206=1358,即所求概率为1358.
团员
非团员
合计
男生
16
9
25
女生
14
6
20
合计
30
15
45
数学选择性必修 第三册第七章 随机变量及其分布7.5 正态分布学案: 这是一份数学选择性必修 第三册<a href="/sx/tb_c4000360_t4/?tag_id=42" target="_blank">第七章 随机变量及其分布7.5 正态分布学案</a>,共16页。
高中人教A版 (2019)第七章 随机变量及其分布7.1 条件概率与全概率公式导学案: 这是一份高中人教A版 (2019)<a href="/sx/tb_c4000356_t4/?tag_id=42" target="_blank">第七章 随机变量及其分布7.1 条件概率与全概率公式导学案</a>,共10页。学案主要包含了典例解析等内容,欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第三册7.1 条件概率与全概率公式优质导学案: 这是一份高中数学人教A版 (2019)选择性必修 第三册7.1 条件概率与全概率公式优质导学案,共6页。学案主要包含了学习目标,自主学习,小试牛刀,经典例题,跟踪训练,当堂达标,参考答案等内容,欢迎下载使用。