2024中考数学几何压轴专题训练-专题06圆形之定理问题（含解析）

这是一份2024中考数学几何压轴专题训练-专题06圆形之定理问题（含解析），共20页。
专题06 圆形之定理问题
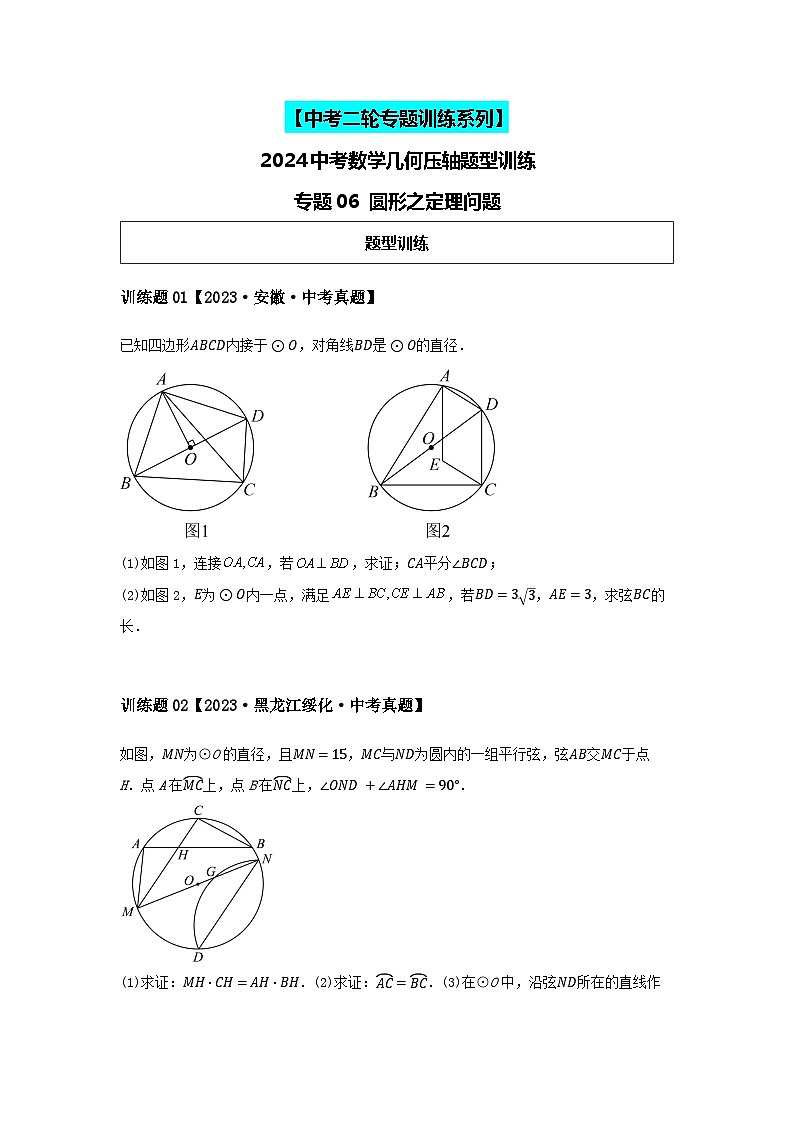
训练题01【2023·安徽·中考真题】
已知四边形ABCD内接于⊙O，对角线BD是⊙O的直径．

(1)如图1，连接，若，求证；CA平分∠BCD；
(2)如图2，E为⊙O内一点，满足，若BD=33，AE=3，求弦BC的长．
训练题02【2023·黑龙江绥化·中考真题】
如图，MN为⊙O的直径，且MN=15，MC与ND为圆内的一组平行弦，弦AB交MC于点H．点A在MC上，点B在NC上，∠OND+∠AHM=90°．

(1)求证：MH⋅CH=AH⋅BH．(2)求证：AC=BC．(3)在⊙O中，沿弦ND所在的直线作劣弧ND的轴对称图形，使其交直径MN于点G．若sin∠CMN=35，求NG的长．
训练题03【2023·北京·中考真题】
如图，是的半径，是的弦，于点D，是的切线，交的延长线于点E．若，，则线段的长为 ．

训练题04【2023·浙江嘉兴·九年级校联考】
阿基米德折弦定理：如图1， AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC>AB，M是ABC的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD=AB+BD．下面是运用“截长法”证明CD=AB+BD的部分证明过程．
证明：如图2，在CB上截取CG=AB，连接MA，MB，MC和MG．∵M是ABC的中点， ∴MA=MC
任务：（1）请按照上面的证明思路，写出该证明的剩余部分；
（2）填空：如图（3），已知等边△ABC内接于⊙O，AB=2，D为⊙O上 一点, ∠ABD=45°，AE⊥BD与点E,则△BDC的周长是 ．
训练题05【2023·陕西咸阳·校考二模】
【问题提出】（1）如图①，AB为⊙O的一条弦，圆心O到弦AB的距离为4，若⊙O的半径为7，则⊙O上的点到弦AB的距离最大值为_______；
【问题探究】（2）如图②，在△ABC中，∠BAC=60°,AD为BC边上的高，若AD=6，求△ABC面积的最小值；
【问题解决】（3）“双减”是党中央、国务院作出的重大决策部署，实施一年多来，工作进展平稳，取得了阶段性成效，为了进一步落实双减政策，丰富学生的课余生活，某校拟建立一块综合实践基地，如图③，△ABC为基地的大致规划示意图，其中∠ABC=90°，BD平分∠ABC交AC于点D，点P为BC上一点，学校计划将四边形ABPD部分修建为农业实践基地，并沿BD铺设一条人行走道，△CDP部分修建为兴趣活动基地．根据规划要求，BD=802米，∠CDP=45°．且农业实践基地部分（四边形ABPD）的面积应尽可能小，问四边形ABPD的面积是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．

训练题06【2022·江苏无锡·中考真题】
如图，边长为6的等边三角形ABC内接于⊙O，点D为AC上的动点（点A、C除外），BD的延长线交⊙O于点E，连接CE．
(1)求证△CED∽△BAD；
(2)当DC=2AD时，求CE的长．
训练题07【2022·广西桂林·中考真题】
如图，某雕塑MN位于河段OA上，游客P在步道上由点O出发沿OB方向行走．已知∠AOB＝30°，MN＝2OM＝40m，当观景视角∠MPN最大时，游客P行走的距离OP是 米．

训练题08【2022·广东深圳·宝安中学校考三模】
弗朗索瓦·韦达是十六世纪法国最杰出的数学家之一，最早提出“切割线定理”（圆幂定理之一），指的是从圆外一点引圆的切线和割线，则切线长是这点到割线与圆交点的两条线段长的比例中项，下面紧跟着圆的切线作图的思路尝试证明与运用．
(1)作图（保留作图痕迹）：
已知AB是圆O的直径，点P是BA延长线上的一点，
①作线段OP的中垂线MN交OP于点Q；
②以Q为圆心，PQ为半径作圆，交圆O于点E、F；
③连接PE和PF；
试说明PE是圆O切线的理由．
(2)计算：
若圆O半径OB=4，PB=14，尝试证明“切割线定理”并计算出PE的长度．
训练题09【2021·湖北随州·中考真题】
如图，在Rt△ABC中，∠ACB=90°，O为AB的中点，OD平分∠AOC交AC于点G，OD=OA，BD分别与AC，OC交于点E，F，连接AD，CD，则OGBC的值为 ；若CE=CF，则CFOF的值为 ．
训练题10【2021·山东济南·中考真题】
已知：如图，AB是⊙O的直径，C，D是⊙O上两点，过点C的切线交DA的延长线于点E，DE⊥CE，连接CD，BC．
（1）求证：∠DAB=2∠ABC；
（2）若tan∠ADC=12，，求⊙O的半径．
题型训练
答案&解析
训练题01【2023·安徽·中考真题】
【答案】(1)见解析
(2)BC=32
【分析】（1）利用垂径定理的推论和圆周角的性质证明即可．
(2)证明四边形AECD平行四边形，后用勾股定理计算即可．
【详解】（1）∵对角线BD是⊙O的直径，
∴AB=AD，
∴，
∴CA平分∠BCD．
（2）∵对角线BD是⊙O的直径，
∴∠BAD=∠BCD=90°，
∴DC⊥BC,DA⊥AB
∵，
∴DC∥AE,DA∥CE，
∴四边形AECD平行四边形，
∴DC=AE=3，
又∵BD=33，
∴BC=332-32=32．
训练题02【2023·黑龙江绥化·中考真题】
【答案】(1)见解析(2)见解析(3)215
【分析】（1）证明△AMH∽△CBH即可；（2）连接OC，交AB于点F，根据平行线的性质和已知条件证明垂直平分即可；（3）利用对称的性质作辅助线，根据已知条件，转化为解直角三角形问题即可．
【详解】（1）∵∠ABC和∠AMC是AC所对的圆周角，∴∠ABC=∠AMC，
∵∠AHM=∠CHB，∴△AMH∼△CBH，∴AHCH=MHBH，∴MH⋅CH=AH⋅BH．
（2）连接OC，交AB于点F，

∵MC与ND为一组平行弦，即：MC∥ND，∴∠OND=∠OMC，
∵OM=OC，∴∠OMC=∠OCM，
∵∠OND+∠AHM=90°，∴∠OCM+∠AHM=∠OCM+∠CHB=90°，
∴∠HFC=90°，∴OC⊥AB，∴OC是AB的垂直平分线，AC=BC．
（3）连接DM、DG，过点D作，垂足为E，设点G的对称点G'，连接G'D、G'N，
∵，∠G'ND=∠GND，∴DM=DG'�，∴DG'=DM，
∴DG=DM，∴△DGM是等腰三角形，
∵，∴GE=ME，∵DN∥CM，∴∠CMN=∠DNM，
∵MN为直径，∴∠MDN=90°，∴∠MDE+∠EDN=90°，
∵，∴∠DEN=90°，∴∠DNM+∠EDN=90°，
sin∠EDM=sin∠DNM=sin∠CMN=35，在Rt△MND中，MN=15，
sin∠DNM=MDMN=35，MD15=35，∴MD=9，
在Rt△MED中，sin∠EDM=35=MEMD，ME9=35∴ME=275，
∴NG=MN-MG=MN-2ME=15-2×275=215∴NG=215故答案为：215．
训练题03【2023·北京·中考真题】
【答案】
【分析】根据，得出，，根据等腰直角三角形的性质得出，即，根据，，得出为等腰直角三角形，即可得出．
【详解】解：∵，
∴，．
∵，
∴为等腰直角三角形，
∴，
∴．
∵是的切线，
∴，
∵，
∴为等腰直角三角形，
∴．
故答案为：．
训练题04【2023·浙江嘉兴·九年级校联考】
【答案】（1）证明见解析；（2）2+22．
【分析】（1）首先证明△MBA≌△MGC，进而得出MB＝MG，再利用等腰三角形的性质得出BD＝GD，即可得出答案；（2）方法一、首先证明△ABF≌△ACD，进而得出AF＝AD，以及CD＋DE＝BE，进而求出DE的长即可得出答案．方法二、先求出，再用（1）的结论得出CD＋DE＝BE，即可得出结论．
【详解】（1）证明：如图2，在CB上截取CG=AB，连接MA，MB，MC和MG．
∵M是ABC的中点， ∴MA=MC

在△MBA和△MGC中BA＝GC∠A＝∠CMA＝MC∴△MBA≌△MGC，∴MB＝MG，
又∵， ∴BD＝GD，∴DC＝GC＋GD＝AB＋BD；
（2）解：方法一、如图3，截取BF＝CD，连接AF，AD，CD，
由题意可得：AB＝AC，∠ABF＝∠ACD，
在△ABF和ACD中AB＝AC∠ABF＝∠ACDBF＝DC，∴△ABF≌△ACD，∴AF＝AD，
∵AE⊥BD，∴FE＝DE，则CD＋DE＝BE，
∵∠ABD＝45°，∴BE=AB2=2，则△BDC的周长是2+22．故答案为2+22．
方法二、∵△ABC是等边三角形，∴BC＝AB＝2，∠ABC＝∠ACB，
∴由（1）的结论得，CD＋DE＝BE，
∵∠ABD＝45°，AB＝2，∴BE=2，∴DE+CE=2，
∴则△BDC的周长是BC＋BD＋CD＝BC＋BE＋DE＋CD＝2+22．故答案为2+22．
训练题05【2023·陕西咸阳·校考二模】
【答案】（1）11；（2）123；（3）四边形ABPD的面积存在最小值，最小值为64002平方米
【分析】（1）根据圆的性质直接可得答案；
（2）作△ABC的外接圆⊙O，连接OA、OB、OC，过点O作OE⊥BC于点E，设OA=OB=OC=R，则OE=12R，根据垂线段最短可得R的最小值，从而得出BC的最小值，进而得出答案；
（3）过点D作DE⊥AB于点E,DF⊥BC于点F，则DE=DF，在BF上截取FG=AE，连接DG，利用SAS证明△DFG≌△DEA，则∴S四边形ABPD=S四边形BEDF+S△DPF+S△DEA=6400+S△DPG，要使四边形ABPD的面积最小，只需△DPG的面积最小，由（2）同理求出△DPG面积的最小值即可．
【详解】解：（1）∵圆心O到弦AB的距离为4，若⊙O的半径为7，
∴⊙O上的点到弦AB的距离最大值为4+7=11，
故答案为：11；
（2）作△ABC的外接圆⊙O，连接OA、OB、OC，过点O作OE⊥BC于点E，如图．

∵∠BAC=60°,∴∠BOC=120°,∴∠OBC=∠OCB=30°．
设OA=OB=OC=R，则OE=12R，
由OA+OE≥AD，得R+12R≥6，即R≥4，
∴BE=OB2-OE2=32R，
∴BC=2BE=3R≥43，
∴SABC=12BC⋅AD≥12×43×6=123．
即△ABC面积的最小值为123
（3）过点D作DE⊥AB于点E,DF⊥BC于点F，
∵BD平分∠ABC，
∴DE=DF．
又∵BD=BD,∠ABD=∠CBD，
∴△BDE≌△BDF．
∵BD=802米，∠DBE=∠DBF12∠ABC=45°，∠BED=∠BFD=90°，
∴△BDE、△BDF为等腰直角三角形，
∴DE=DF=BE=BF=80米，
∴SBDE=12BE⋅DE=3200（平方米），
S四边形BEDF=2S△BDE=6400平方米．
在BF上截取FG=AE，连接DG，如图．

∵FG=AE,∠DFG=∠DEA=90°,DF=DE，
∴△DFG≌△DEASAS，
∴S四边形ABPD=S四边形BEDF+S△DPF+S△DEA=6400+S△DPG，
∴要使四边形ABPD的面积最小，只需△DPG的面积最小．
∵∠CDP=45°,∴∠ADP=180°-45°=135°，
∴∠ADE+∠PDF=∠PDG=45°，
作△DPG的外接圆⊙O，如图，连接OP、OD、OG，作OH⊥PG于点H，
则∠POG=2∠PDG=90°，
∴∠POH=∠GOH=45°．
设OH=m，则OP=OD=OG=2m,PG=2m．
由OD+OH≥DF，得m+2m≥80，解得m≥801+2，
∴PG≥1601+2米，
∴SPDG=12PG⋅DF≥12×1601+2×80=64002-6400（平方米），
∴S四边形ABPD≥6400+64002-6400=64002（平方米）．
即四边形ABPD的面积存在最小值，最小值为64002平方米．
训练题06【2022·江苏无锡·中考真题】
【答案】(1)见解析
(2)CE=1277
【分析】（1）根据同弧所对圆周角相等可得∠A=∠E，再由对顶角相等得∠BDA=∠CDE，故可证明绪论；
（2）根据DC=2AD可得AD=2,CD=4，由△CED∽△BAD可得出BD·DE=8,连接AE，可证明△ABD∽△EBA，得出AB2=BD·BE=BD2+BD·BE, 代入相关数据可求出BD=27，从而可求出绪论．
【详解】（1）∵BC所对的圆周角是∠A,∠E，
∴∠A=∠E，
又∠BDA=∠CDE，
∴△CED∽△BAD；
（2）∵△ABC是等边三角形，
∴AC=AB=BC=6
∵DC=2AD，
∴AC=3AD,
∴AD=2,DC=4,
∵ΔCED~ΔBAD,
∴ADDE=BDCD=ABCE，
∴2DE=BD4,
∴BD⋅DE=8;
连接AE,如图，
∵AB=BC,
∴AB=BC
∴∠BAC=∠BEA,
又∠ABD=∠EBA，
∴△ABD~ΔEBA,
∴ABBE=BDAB，
∴AB2=BD⋅BE=BD⋅(BD+DE) =BD2+BD⋅DE,
∴62=BD2+8，
∴BD=27（负值舍去）
∴6CE=274，
解得，CE=1277
训练题07【2022·广西桂林·中考真题】
【答案】203
【分析】先证OB是⊙F的切线，切点为E，当点P与点E重合时，观景视角∠MPN最大，由直角三角形的性质可求解．
【详解】解：如图，取MN的中点F，过点F作FE⊥OB于E，以直径MN作⊙F，

∵MN＝2OM＝40m，点F是MN的中点，∴MF＝FN＝20m，OF＝40m，
∵∠AOB＝30°，EF⊥OB，∴EF＝20m，OE＝3EF＝203m，∴EF＝MF，
又∵EF⊥OB，∴OB是⊙F的切线，切点为E，
∴当点P与点E重合时，观景视角∠MPN最大，此时OP＝203m，故答案为：203．
训练题08【2022·广东深圳·宝安中学校考三模】
【答案】(1)见解析
(2)证明见解析，EP=221
【分析】（1）按要求作图，根据MN是OP的中垂线，得到OQ=OP，点O在圆Q上，OQ=EQ=PQ，根据三角形内角和定理和等腰三角形的性质可得∠OEP=90°，即可证明；
（2）根据切线的性质和圆周角定理的推论可得∠EBO=∠AEP，证得△AEP∽△EBP，所以APEP=EPBP，EP2=AP·BP，根据OB=4，PB=14，求出AP的长度，代入计算即可．
【详解】（1）作图如下：
连接OE，EQ，
∵以Q为圆心，PQ为半径作圆，交圆O于点E、F；
∴QE=QP，
∵MN是OP的中垂线，
∴OQ=OP，点O在圆Q上，
∴OQ=EQ=PQ，
∴∠EOQ=∠OEQ，∠PEQ=∠EPQ，
∵∠EOP+∠OEQ+∠QEP+∠EPQ=180°，
∴2（∠OEQ+∠QEP）=180°，
∴∠OEQ+∠QEP=90°，即∠OEP=90°，OE垂直EP，
∴PE是圆O的切线．
（2）证明：连接BE，OA，
∵EP是圆O的切线， AB为圆O的直径，
∴∠OEP=90°，∠BEA=90°，
∴∠BEO=∠AEP
∵OE和OB为圆O的半径，
∴∠BEO=∠EBO，
∴∠EBO=∠AEP，
∵∠EPB=∠EPA，
∴△AEP∽△EBP，
∴APEP=EPBP，
∴EP2=AP·BP．
∵OB=4，PB=14，
∴AB=2OB=8，AP=BP－AB=14－8=6，
∴EP2=6×14=84，
∴EP=221．
训练题09【2021·湖北随州·中考真题】
【答案】 12 2
【分析】（1）根据条件，证明△AOD≅△COD，从而推断∠OGA=90∘，进一步通过角度等量，证明△AOG∼△ABC，代入推断即可.（2）通过OA=OD=OC=OB，可知 四点共圆，通过角度转化，证明△ODF∼△CBF，代入推断即可.
【详解】解：（1）∵∠ACB=90°，O为AB的中点∴OA=OC 又∵OD平分∠AOC∴∠AOD=∠COD
又∵OD=OD ∴△AOD≅△COD ∴AD=CD ∴OD⊥AC ∴∠OGA=90∘
在△AOG与△ABC中∠GAO=∠BAC,∠OGA=∠BCA=90∘∴△AOG∼△ABC OGBC=AOAB=12
（2∵OA=OD=OC=OB ∴ 四点共圆，如下图：
∵CE=CF∴∠CEF=∠CFE 又∵ ∴∠CEF=∠BFO
∵△AOD≅△COD∴AD=CD∴AD=CD ∴∠OBF=∠CBE
∴∠BFO+∠OBF=∠CEF+∠CBE=90∘ 即
∵OB=OC ∴BC=2OC=2OA=2OD ∵∠OGA=∠BCA=90∘ ∴∠ODB=∠FBC
∵∠OFD=∠CFB ∴△ODF∼△CBF ∴CFOF=BCOD=2故答案为：12；2
训练题10【2021·山东济南·中考真题】
【答案】（1）见解析；（2）5
【分析】（1）连接OC，根据切线的性质，已知条件可得DE//OC，进而根据平行线的性质可得∠DAB=∠AOC，根据圆周角定理可得∠AOC=2∠ABC，等量代换即可得证；
（2）连接AC，根据同弧所对的圆周角相等，可得∠D=∠B，进而根据正切值以及已知条件可得AC的长，勾股定理即可求得AB，进而即可求得圆的半径．
【详解】（1）连接OC，如图，
∵是⊙O的切线，
∴OC⊥CE，
∵DE⊥CE，
∴OC//DE，
∴∠DAB=∠AOC，
∵AC=AC，
∴∠AOC=2∠ABC，
∴∠DAB=2∠ABC．
（2）连接AC
∵AB是⊙O的直径，
，
∵AC=AC，
∴∠ADC=∠ABC，
tan∠ADC=12，
∴tan∠ABC=12=ACBC，
∵，
∴AC=2，
，
∴AO=12AB=5．
即⊙O的半径为5．