湖南省张家界市慈利县2024届九年级上学期期中教学质量检测数学试卷(含解析)

这是一份湖南省张家界市慈利县2024届九年级上学期期中教学质量检测数学试卷(含解析)，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
考生注意：全卷共有三道大题，满分120分，时量120分钟．
一、选择题（每小题3分，共10道小题，合计30分）
1. 下列函数是反比例函数的是（ ）
A. B. C. D.
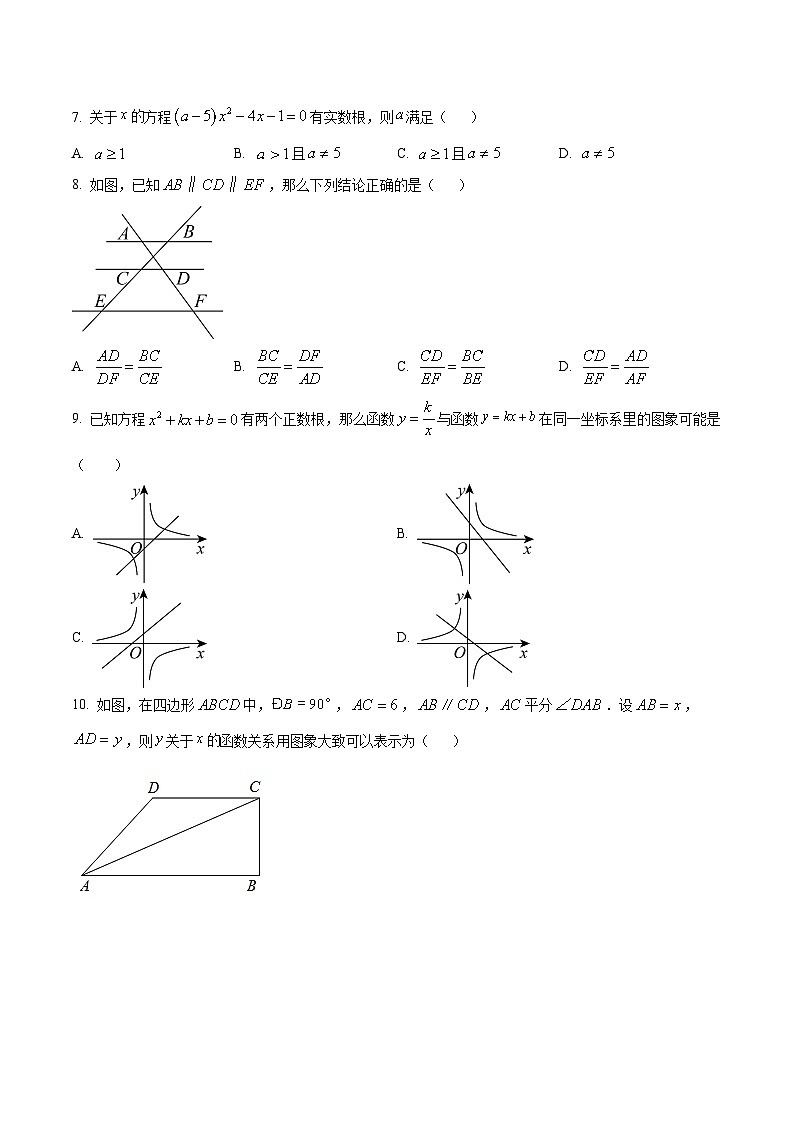
2. 若x＝1是关于x的一元二次方程x2+mx﹣3＝0的一个根，则m的值是（ ）
A. ﹣2B. ﹣1C. 1D. 2
3. 下列四组长度的线段中，是成比例线段的是（ ）
A. 4cm，5cm，6cm，7cmB. 3cm，4cm，5cm，8cm
C. 5cm，15cm，3cm，9cmD. 8cm，4cm，1cm，3cm
4. 已知点，，三点都在反比例函数的图像上，则下列关系正确的是（ ）
A. B. C. D.
5. 生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下与全身的高度比值接近0．618，可以增加视觉美感，若图中为2米，则约为（ ）
A. 1．24米B. 1．38米C. 1．42米D. 1．62米
6. 用配方法解方程时，原方程应变形为( )
A. B. C. D.
7. 关于方程有实数根，则满足（ ）
A. B. 且C. 且D.
8. 如图，已知，那么下列结论正确的是（ ）
A. B. C. D.
9. 已知方程有两个正数根，那么函数与函数在同一坐标系里的图象可能是（ ）
A. B.
C. D.
10. 如图，在四边形中，，，，平分．设，，则关于函数关系用图象大致可以表示为（ ）
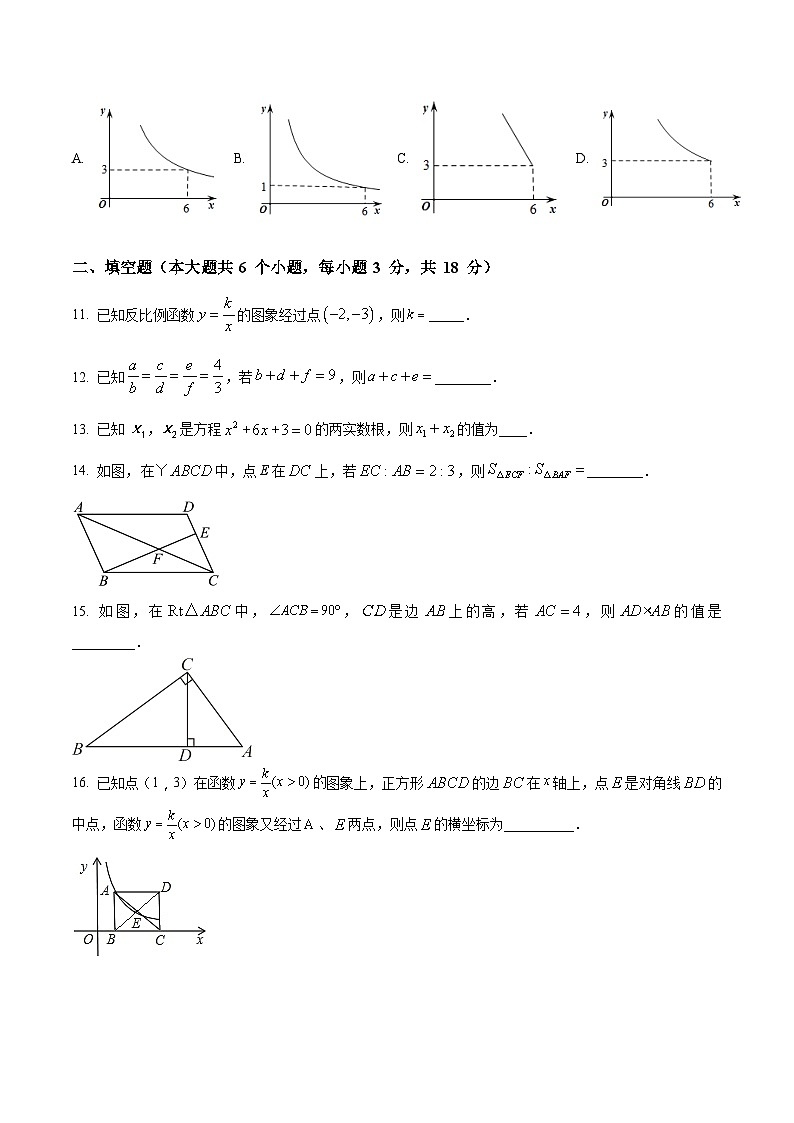
A. B. C. D.
二、填空题（本大题共 6 个小题，每小题 3 分，共 18 分）
11. 已知反比例函数的图象经过点，则_____．
12. 已知，若，则________．
13. 已知 ，是方程的两实数根，则的值为____．
14. 如图，中，点E在上，若，则________．

15. 如图，在中，，是边上的高，若，则的值是_________．
16. 已知点（1，3）在函数图象上，正方形的边在轴上，点是对角线的中点，函数的图象又经过、两点，则点的横坐标为__________．
三、解答题（本大题共9小题，共72分）
17. 解方程
（1）；
（2）．
18. 如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上、已知纸板的两条边DF＝0.5m，EF＝0.3m，测得边DF离地面的高度AC＝1.5m，CD＝10m，求树高AB．
19. 已知某蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．
（1）求这个反比例函数的解析式；
（2）如果以此蓄电池为电源的用电器的限制电流不能超过3A，那么用电器可变电阻应控制在什么范围？
20. 如图，在中，，D是边上一点，．求证．
21. 某超市于今年年初以每件25元的进价购进一批商品．当商品售价为40元时，一月份销售256件．二、三月该商品十分畅销．销售量持续走高．在售价不变的基础上，三月底的销售量达到400件．设二、三这两个月的月平均增长率不变．
（1）求二、三这两个月的月平均增长率；
（2）从四月份起，商场决定采用降价促销的方式回馈顾客，经调查发现，该商品每降价1元，销售量增加5件，当商品降价多少元时，商场获利4250元？
22. 关于x的一元二次方程．
（1）证明：不论m为何值，方程总有两个不相等的实数根；
（2）若方程的两根为且满足，求m的值．
23. 如图，已知中，，点D是边上一点，且．

（1）求证：；
（2）求证：．
24. 如图，已知一次函数的图象与轴、轴分别交于，两点，与反比例函数的图象分别交于两点．
（1）求一次函数与反比例函数的解析式；
（2）当时，求自变量x的取值范围；
（3）若点在轴上，且，求点的坐标．
25. 如图，在四边形中， ， ， ， ， ，动点P从点D出发，沿线段 的方向以每秒2个单位长的速度运动；动点Q从点 C出发，在线段 上以每秒1个单位长的速度向点 运动；点P， 分别从点D，C同时出发，当点 运动到点 时，点Q随之停止运动，设运动的时间为t秒）.
（1）当 时，求 的面积；
（2）若四边形为平行四边形，求运动时间 .
（3）当 为何值时，以 B、P、Q为顶点三角形是等腰三角形？
二○二三秋季期中教学质量检测
九年级 数学答案
一、选择题（每小题3分，共10道小题，合计30分）
1. B
解：A、，是正比例函数，不是反比例函数；
B、是反比例函数；
C、不是反比例函数；
D、不是反比例函数；
故选：B.
2. D
解：把x=1代入方程x2+mx-3=0得：1+m-3=0，
解得：m=2．
故选：D．
3. C
解析：A、∵，∴4cm，5cm，6cm，7cm不是成比例线段，故该选项不符合题意；
B、∵，∴3cm，4cm，5cm，8cm不是成比例线段，故该选项不符合题意；
C、∵，∴5cm，15cm，3cm，9cm是成比例线段，故该选项符合题意；
D、∵，∴8cm，4cm，1cm，3cm不是成比例线段，故该选项不符合题意；
故选C．
4. C
解析：∵，
∴，，
∴．
故选C．
5. A
解析：由题意可知，a:b≈0.618，代入b=2，
∴a≈2×0.618=1.236≈1.24．
故答案为：A
6. A
解析：，
，
；
故选：A．
7. A
解析：分类讨论：
当即时，方程变为，此时方程一定有实数根；
当即时，
关于的方程有实数根
，
．
的取值范围为．
故选：A．
8. A
解析：∵，
∴，选项A正确，符合题意；
选项B错误，不符合题意；
∵，
∴，
∴，
∴选项C、D均错误，不符合题意；
故选：A．
9. D
解析：∵方程有两个正数根，
∴两根之和为，两根之积为，
∴，，
∴函数的图象过二，四象限，函数的图象过一、二、四象限，
∴满足题意的，只有选项D．
故选D．
10. D
解析：∵，∴，
∵平分，∴，
∴，则，即为等腰三角形，
过点做于点．
则垂直平分，，，
∵，，
∴，
∴，
∴，
∴，
∵在中，，
∴，
故选D．
二、填空题（本大题共 6 个小题，每小题 3 分，共 18 分）
11. 6
解析：由，得，
反比例函数图象经过点，
．
故答案为：6．
12. 12
解析：，
由等比性质，得，
所以．
故答案为：12．
13.
解析：由题意得：，
故答案为：．
14.
解析：中，，
，，
，
，
即，
故答案为：．
15. 16
解析：∵，于点D，
∴，，
∴，
又∵，
∴，
∴，而，
∴，
故答案为：16．
16.
解析：把(1,3)代入到y=得：k=3，
故函数解析式为y=，
设A(a, )(a>0),根据图象和题意可知,点E(a+,)，
因为y=的图象经过E，
所以将E代入到函数解析式中得： (a+)=3，
即=，
求得：a=或a=− (不合题意,舍去)，
∴a=，
∴a+=，
则点E的横坐标为.
故答案为.
三、解答题（本大题共9小题，共72分）
17. （1）解：，
∴，
∴或，
解得：，；
（2），
∴，
∴，
∴，
∴，
解得：，．
18. 解：∵∠DEF＝∠BCD＝90°，∠D＝∠D，
∴△DEF∽△DCB，
∴，
∵DF＝0.5 m，EF＝0.3 m，AC＝1.5 m，CD＝10 m，
由勾股定理得DE＝＝0.4 m，
∴，
∴BC＝7.5m，
∴AB＝AC+BC＝1.5+7.5＝9（m），
答：树高AB是9m．
19. （1）解：（1）电流I是电阻R的反比例函数，设I=，
∵图象经过（20，1.8），
∴1.8=，
解得k=1.8×20=36，
∴I=；
（2）解：∵I≤3，I=，
∴≤3，
∴R≥12，
即用电器可变电阻应控制在12Ω以上的范围内．
20.证明：∵，，
∴．
∴．
∵，
∴．
21.（1）解：设二、三这两个月的月平均增长率为x，根据题意可得：
，
解得：，（不合题意舍去）．
答：二、三这两个月的月平均增长率为；
（2）解：设当商品降价m元时，商品获利4250元，根据题意可得：
，
解得：，（不合题意舍去）．
答：当商品降价5元时，商品获利4250元．
22. （1）∵
∴不论m为何值，方程总有两个不相等的实数根；
（2）∵方程的两根为
∴,
∵
∴
解得：
23.（1）证明：，
∴，，
，
，
，
．
（2）证明：，
，
由（1）知：，
，
，
，
．
24. （1）解：将的坐标代入反比例函数得，
，
∴反比例函数的关系式为，
将，的坐标代入一次函数得，
，
解得，
∴一次函数的关系式为，
（2）由于方程组
的解为，，
∴一次函数与反比例的交点坐标为和(-4，)，
又∵，
∴，
∴当时，自变量x的取值范围是或，
故答案为：或；
（3）∵
，
设点，则，
由，
，
解得或，
∴点或．
25.（1）过点作于，则四边形为矩形．
，
，
．
把代入得到：；
（2）当四边形是平行四边形时，，
即，
解得：，
当时，四边形是平行四边形．
（3）由图可知，，，若以、、为顶点的三角形是等腰三角形，可以分三种情况：
①若，在中，，由得，解得；
②若，在中，，由得，即，
此时，△，
所以此方程无解，．
③若，由得得，（不合题意，舍去）．
综上所述，当或时，以，，三点为顶点的三角形是等腰三角形．