第6章 实数 复习小结 七年级下册大单元教学课件

这是一份第6章 实数 复习小结 七年级下册大单元教学课件，共22页。

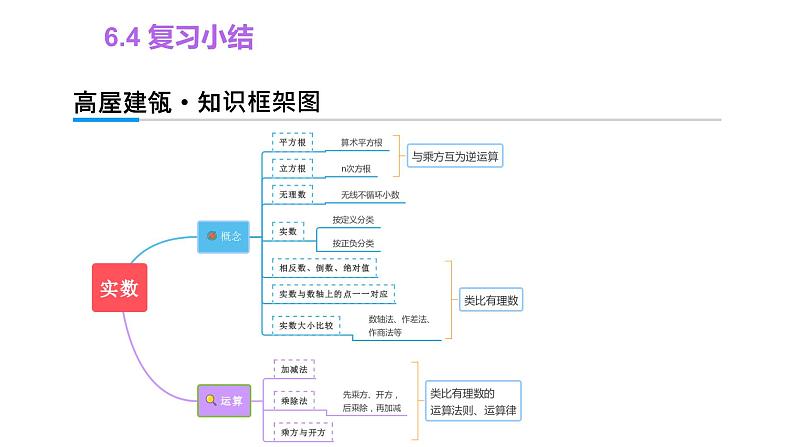
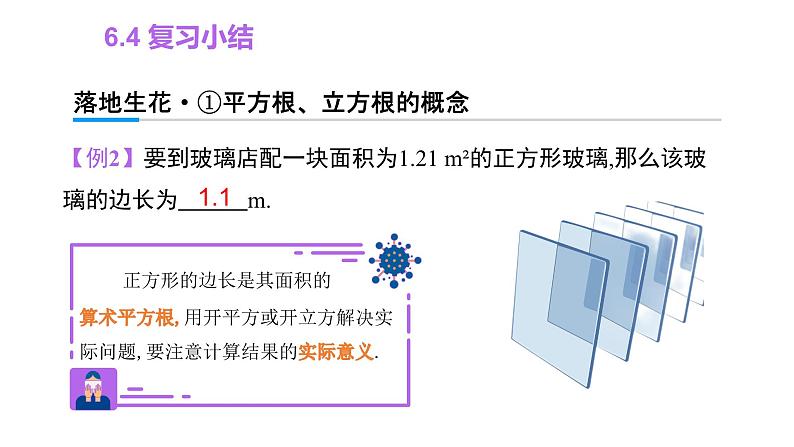
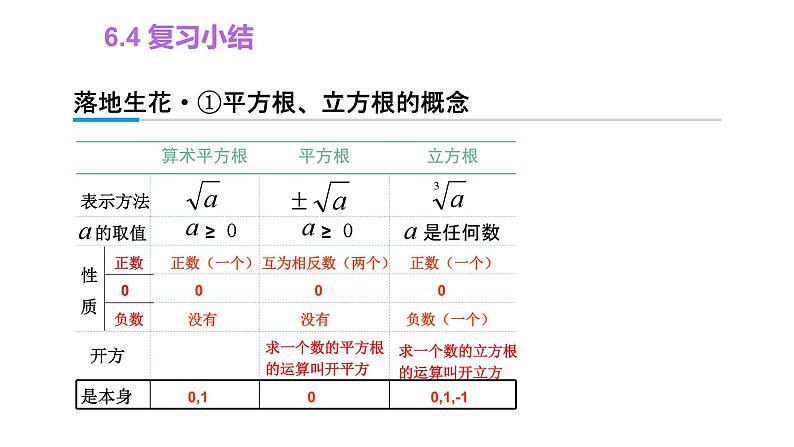
6.4复习小结6.4 复习小结高屋建瓴·知识框架图6.4 复习小结落地生花·①平方根、立方根的概念【例1】1. 求下列各数的平方根：2. 求下列各数的立方根：【归纳拓展】解题时，要注意题目的要求，是求平方根、立方根还是求算术平方根，要注意所求结果处理.6.4 复习小结落地生花·①平方根、立方根的概念6.4 复习小结落地生花·①平方根、立方根的概念【变式2】（1）求下列各式的值：答案：（2）填空：64±8-4-4,-3,-2,-1,0,1,2,36.4 复习小结落地生花·①平方根、立方根的概念【例2】要到玻璃店配一块面积为1.21 m²的正方形玻璃,那么该玻璃的边长为　　　m.1.16.4 复习小结落地生花·①平方根、立方根的概念【变式3】已知b=a3+2c,其中b的算术平方根为19,c的平方根是±3,求a的值.解:因为b的算术平方根是19,所以b=192=361.因为c的平方根是±3,所以c=(±3)2=9.所以a3=b-2c=361-18=343, a=7.6.4 复习小结落地生花·①平方根、立方根的概念表示方法性质开方正数0负数正数（一个）0没有互为相反数（两个）0没有正数（一个）0负数（一个）求一个数的平方根的运算叫开平方求一个数的立方根的运算叫开立方是本身0,100,1,-16.4 复习小结落地生花·②实数的有关概念A. 1 B. 2 C. 3 D. 4【归纳拓展】对实数进行分类不能只看表面形式，应先化简，再根据结果去判断.B6.4 复习小结落地生花·②实数的有关概念A. 1 个 B. 2 个 C. 3 个 D. 4 个AB6.4 复习小结落地生花·③实数的估算与大小比较【例4】(1) 位于相邻整数 和 之间. (2) 实数 a，b 在数轴上的位置如图所示，化简= .-2a【归纳拓展】1. 实数与数轴上的点是一一对应的关系；2. 在数轴上表示的数，右边的数总是比左边的数大.456.4 复习小结落地生花·③实数的估算与大小比较= .6.4 复习小结落地生花·③实数的估算与大小比较【例5】比较 与 的大小. 解:【变式6】比较 与 的大小. 解:6.4 复习小结落地生花·④实数的运算【例6】（1） ； （2） .60y - 1【例7】已知 ， ， ，则 = __， = . 0.0813837.77【例8】计算： = .【归纳拓展】开立方运算时要注意小数点的变化规律，开立方是三位与一位的关系，开平方是二位与一位的关系.6.4 复习小结锦上添花·⑤数形结合【例9】实数a,b在数轴上的位置如图所示,化简 解析:去绝对值和根号,此时只要分别判断a+b和b-a的符号即可.解:由图可知a<0,b>0,且|a|>|b|.所以a+b<0 , b-a>0,所以原式=-(a+b)+(b-a)=-2a.6.4 复习小结锦上添花·⑤数形结合【变式7】已知数轴上有A,B两点,且这两点之间的距离为 ,若点A在数轴上表示的数为 ,则点B在数轴上表示的数为 　　 　.  解析：本题运用绝对值的知识来解，若数轴上A点表示的数为a,B点表示的数为b，则A、B两点之间的距离为|a－b|，设B点在数轴上表示的数为b,则| －b|= ，解得b= 或 .6.4 复习小结锦上添花·⑥非负数的性质及应用【例10】若 与 互为相反数，则 　　 　.  解：6.4 复习小结锦上添花·⑥非负数的性质及应用【变式8】若 与 互为相反数，则 　　 　.  解：6.4 复习小结学以致用·刻意练习 1. 写出两个大于 1 小于 4 的无理数____、____. 2. 的整数部分为____,小数部分为_ ____. 3. 一个立方体的棱长是 4 cm，若把它的体积扩大为 原来的 8 倍，则扩大后的立方体的表面积是______.36.4 复习小结学以致用·刻意练习4. 求下列各式中的 x.（1）(x - 1)2 = 64； （2） .( x = 9 或 -7 )( x = -18 )6.4 复习小结学以致用·刻意练习解：∵ |3a + 4|≥0，且 (4b - 3)2≥0，而 |3a + 4| + (4b - 3)2 = 0，∴ |3a + 4| = 0，且 (4b - 3)2 = 0.∴ a = ，b = .∴ -ab = -( × ) = 1.∴ 1 的平方根是 ±1.6.4 复习小结学以致用·刻意练习7.计算：解：原式 = 3.6.解：原式 = -4.