初中数学北师大版八年级下册3 线段的垂直平分线课时训练

这是一份初中数学北师大版八年级下册3 线段的垂直平分线课时训练，共13页。
1. 理解线段垂直平分线的概念.
2. 探索并证明线段垂直平分线的性质定理.
【知识点梳理】
知识点1 ：线段垂直平分线
1.定义
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫线段的中垂线。
2.线段垂直平分线的作图
1. 分别以点 A、B 为圆心，以大于AB 的长为半径作弧，两弧相交于 C、D 两点；
2. 作直线 CD，CD 为所求直线

知识点2 ：线段垂直平分线性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
知识点3：线段的垂直平分线逆定理
到一条线段两个端点距离相等的点，在这条线段的垂直平分线上
【典例分析】
【考点1 ：垂直平分线的性质】
【典例1】（秋•慈溪市期末）如图，△ABC中，DE是AC的垂直平分线，AE＝5，△ABD的周长为16，则△ABC的周长为（ ）
A．18B．21C．24D．26
【变式1-1】（2021春•罗湖区校级期末）如图，在△ABC中，BC＝8，AB的垂直平分线分别交AB、AC于点D、E，△BCE的周长为18，则AC的长等于（ ）
A．12B．10C．8D．6
【变式1-2】（大石桥市模拟）如图，△ABC中，DE是AC的垂直平分线，AE＝4cm，△ABD的周长为14cm，则△ABC的周长为（ ）
A．18 cmB．22 cmC．24 cmD．26 cm
【变式1-3】（2021春•高明区校级期末）如图，在△ABC中，边AB的垂直平分线分别交AB、BC于点D、E，边AC的垂直平分线分别AC、BC于点F、G、若BC＝4，则△AEG的周长为（ ）
A．12B．10C．8D．4
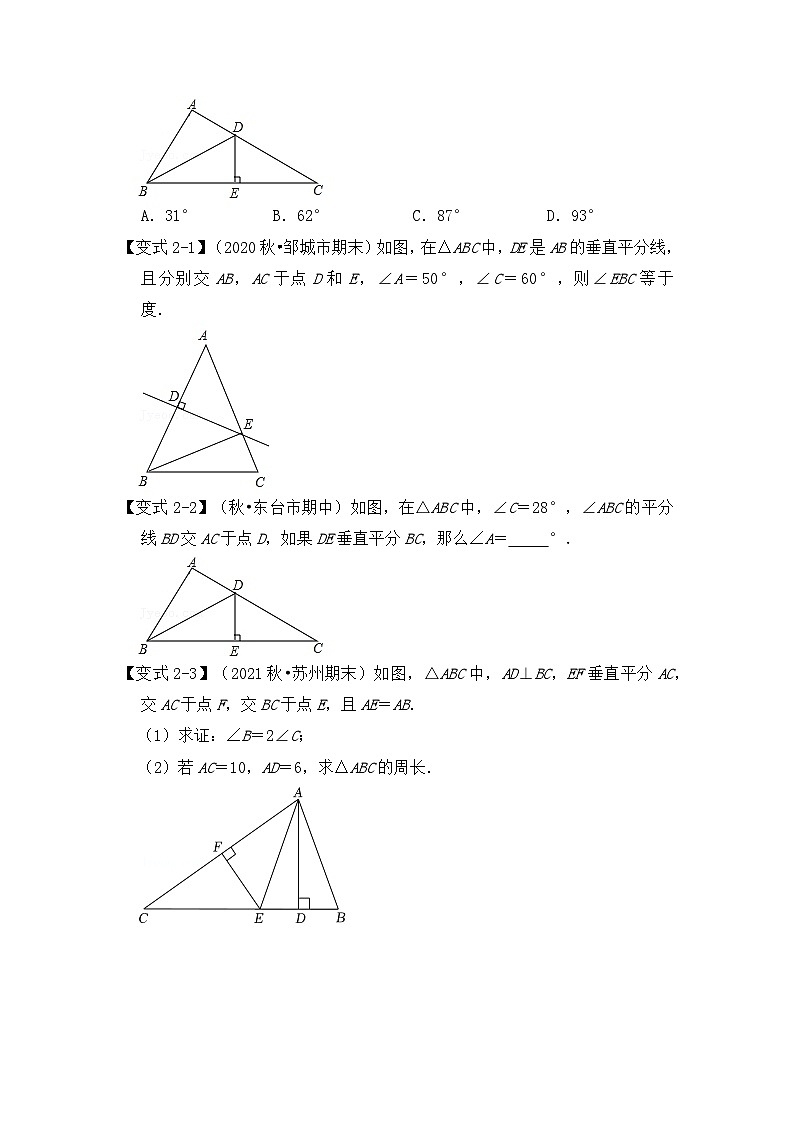
【典例2】（2021春•崂山区期末）如图，在△ABC中，∠C＝31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A的度数为（ ）
A．31°B．62°C．87°D．93°
【变式2-1】（2020秋•邹城市期末）如图，在△ABC中，DE是AB的垂直平分线，且分别交AB，AC于点D和E，∠A＝50°，∠C＝60°，则∠EBC等于 度．
【变式2-2】（秋•东台市期中）如图，在△ABC中，∠C＝28°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A＝ °．
【变式2-3】（2021秋•苏州期末）如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且AE＝AB．
（1）求证：∠B＝2∠C；
（2）若AC＝10，AD＝6，求△ABC的周长．
【考点2：垂直平分线的逆定理】
【典例3】如图，已知AB=AC,∠ABD=∠ACD，求证：AD是线段BC的垂直平分线．
【变式3】如图，P是∠MON的平分线上的一点，PA⊥OM,PB⊥ON,垂足分别为A、B．求证：PO垂直平分AB．
【考点3：尺规作图】
【典例5】电信部门要修建一座电视信号发射塔P，按照设计要求，发射塔P到两城镇A、B的距离必须相等，到两条高速公路m和n的距离也必须相等．请在图中作出发射塔P的位置．（尺规作图，不写作法，保留作图痕迹）
【变式5】（2020秋•西山区期末）尺规作图：已知∠AOB和C，D两点，请在图中用尺规作图找出一点E，使得点E到OA，OB的距离相等，而且E点到C，D的距离也相等．（不写作法，保留作图痕迹）
专题1.4 垂直平分线（知识解读）
【学习目标】
1. 理解线段垂直平分线的概念.
2. 探索并证明线段垂直平分线的性质定理.
【知识点梳理】
知识点1 ：线段垂直平分线
1.定义
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫线段的中垂线。
2.线段垂直平分线的作图
1. 分别以点 A、B 为圆心，以大于AB 的长为半径作弧，两弧相交于 C、D 两点；
2. 作直线 CD，CD 为所求直线

知识点2 ：线段垂直平分线性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
知识点3：线段的垂直平分线逆定理
到一条线段两个端点距离相等的点，在这条线段的垂直平分线上
【典例分析】
【考点1 ：垂直平分线的性质】
【典例1】（秋•慈溪市期末）如图，△ABC中，DE是AC的垂直平分线，AE＝5，△ABD的周长为16，则△ABC的周长为（ ）
A．18B．21C．24D．26
【答案】D
【解答】解：∵DE是AC的垂直平分线，
∴DA＝DC，AE＝CE＝5，
而△ABD的周长是16，即AB+BD+AD＝16，
∴AB+BC+AC＝AB+BD+CD+AC＝16+10＝26，
即△ABC的周长是26．
故选：D
【变式1-1】（2021春•罗湖区校级期末）如图，在△ABC中，BC＝8，AB的垂直平分线分别交AB、AC于点D、E，△BCE的周长为18，则AC的长等于（ ）
A．12B．10C．8D．6
【答案】B
【解答】解：∵DE是AB的垂直平分线，
∴EA＝EB，
由题意得，BC+CE+BE＝18，
则BC+CE+AE＝18，即BC+AC＝18，又BC＝8，
∴AC＝10，
故选：B．
【变式1-2】（大石桥市模拟）如图，△ABC中，DE是AC的垂直平分线，AE＝4cm，△ABD的周长为14cm，则△ABC的周长为（ ）
A．18 cmB．22 cmC．24 cmD．26 cm
【答案】B
【解答】解：∵DE是AC的垂直平分线，
∴DA＝DC，AE＝EC＝4cm，
而△ABD的周长为14cm，即AB+BD+AD＝14cm，
∴AB+BD+DC＝14cm，
∴AB+BC+AC＝14cm+8cm＝22cm，
即△ABC的周长为22cm．
故选：B．
【变式1-3】（2021春•高明区校级期末）如图，在△ABC中，边AB的垂直平分线分别交AB、BC于点D、E，边AC的垂直平分线分别AC、BC于点F、G、若BC＝4，则△AEG的周长为（ ）
A．12B．10C．8D．4
【答案】D
【解答】解：∵ED，GF分别是AB，AC的垂直平分线，
∴AE＝BE，AG＝GC，
∴△AEG的周长为AE+AG+EG＝BC＝4．
故选：D．
【典例2】（2021春•崂山区期末）如图，在△ABC中，∠C＝31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A的度数为（ ）
A．31°B．62°C．87°D．93°
【答案】C
【解答】解：∵DE垂直平分BC，
∴DB＝DC，
∴∠DBC＝∠C＝31°，
∵BD平分∠ABC，
∴∠ABD＝∠CBD＝31°，
∴∠A＝180°﹣31°×3＝87°，
故选：C．
【变式2-1】（2020秋•邹城市期末）如图，在△ABC中，DE是AB的垂直平分线，且分别交AB，AC于点D和E，∠A＝50°，∠C＝60°，则∠EBC等于 度．
【答案】20
【解答】解：∵A＝50°，∠C＝60°，
∴∠ABC＝180°﹣50°﹣60°＝70°，
∵DE是AB的垂直平分线，
∴EA＝EB，
∴∠EBA＝∠A＝50°，
∴∠EBC＝∠ABC﹣∠EBA＝70°﹣50°＝20°，
故答案为：20．
【变式2-2】（秋•东台市期中）如图，在△ABC中，∠C＝28°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A＝ °．
【答案】96
【解答】解：∵DE垂直平分BC，
∴DB＝DC，
∴∠DBC＝∠C＝28°，
∵BD是∠ABC的平分线，
∴∠ABD＝∠DBC＝28°，
∴∠A＝180°﹣28°×3＝96°，
故答案为：96°．
【变式2-3】（2021秋•苏州期末）如图，△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且AE＝AB．
（1）求证：∠B＝2∠C；
（2）若AC＝10，AD＝6，求△ABC的周长．
【解答】解：（1）∵AD⊥BC，AE＝AB，EF垂直平分AC，
∴AB＝AE＝EC，
∴∠C＝∠CAE，∠B＝∠AEB，
∴∠B＝∠AEB＝∠C+∠CAE＝2∠C．
（2）在直角三角形ACD中，
∵∠ADC＝90°，
∴＝8，
∵AD⊥BC，AE＝AB，EF垂直平分AC，
∴AB＝AE＝EC，DE＝BE，
∴AB+BC＝AB+BD+DE+CE＝2DE+2CE＝2CD＝2×8＝16，
∴△ABC的周长＝AB+BC+AC＝16+10＝26．
【考点2：垂直平分线的逆定理】
【典例3】如图，已知AB=AC,∠ABD=∠ACD，求证：AD是线段BC的垂直平分线．
【解析】证明：∵ AB=AC（已知）
∴∠ABC=∠ACB (等边对等角)
又∵∠ABD=∠ACD (已知)
∴∠ABD-∠ABC =∠ACD-∠ACB (等式性质)
即 ∠DBC=∠DCB
∴DB=DC （等角对等边）
∵AB=AC（已知）
DB=DC（已证）
∴点A和点D都在线段BC的垂直平分线上（和一条线段两个端点距离相等的点，在这条线段的垂直平分线上）
∴AD是线段BC的垂直平分线。
【变式3】如图，P是∠MON的平分线上的一点，PA⊥OM,PB⊥ON,垂足分别为A、B．求证：PO垂直平分AB．
【解析】证明：∵OP是角平分线，
∴∠AOP=∠BOP
∵PA⊥OM,PB⊥ON,
∴∠OAP=∠OBP=90°
∴在△AOP 和△BOP中
∴△AOP≌△BOP（AAS）
∴OA=OB
∴PO垂直平分AB（和一条线段两个端点距离相等的点，在这条线段的垂直平分线上）.
【考点3：尺规作图】
【典例5】电信部门要修建一座电视信号发射塔P，按照设计要求，发射塔P到两城镇A、B的距离必须相等，到两条高速公路m和n的距离也必须相等．请在图中作出发射塔P的位置．（尺规作图，不写作法，保留作图痕迹）
【解析】解：设两条公路相交于O点．P为线段AB的垂直平分线与∠MON的平分线交点或是与∠QON的平分线交点即为发射塔的位置．如图，满足条件的点有两个，即P、P′．
【变式5】（2020秋•西山区期末）尺规作图：已知∠AOB和C，D两点，请在图中用尺规作图找出一点E，使得点E到OA，OB的距离相等，而且E点到C，D的距离也相等．（不写作法，保留作图痕迹）
【答案】略
【解答】解：如图，点E即为所求．
因为点E到OA，OB的距离相等，而且E点到C，D的距离也相等，
所以作CD的垂直平分线，∠AOB的角平分线，
两条线相交于点E．