模拟真题湖南省怀化市中考数学三年高频真题汇总 卷（Ⅰ）（含答案及解析）

这是一份模拟真题湖南省怀化市中考数学三年高频真题汇总 卷（Ⅰ）（含答案及解析），共25页。试卷主要包含了如图，点B，有理数 m等内容，欢迎下载使用。
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、一元二次方程的根为（ ）
A．B．C．D．
2、利用如图①所示的长为a、宽为b的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的等式为（ ）
A．B．
C．D．
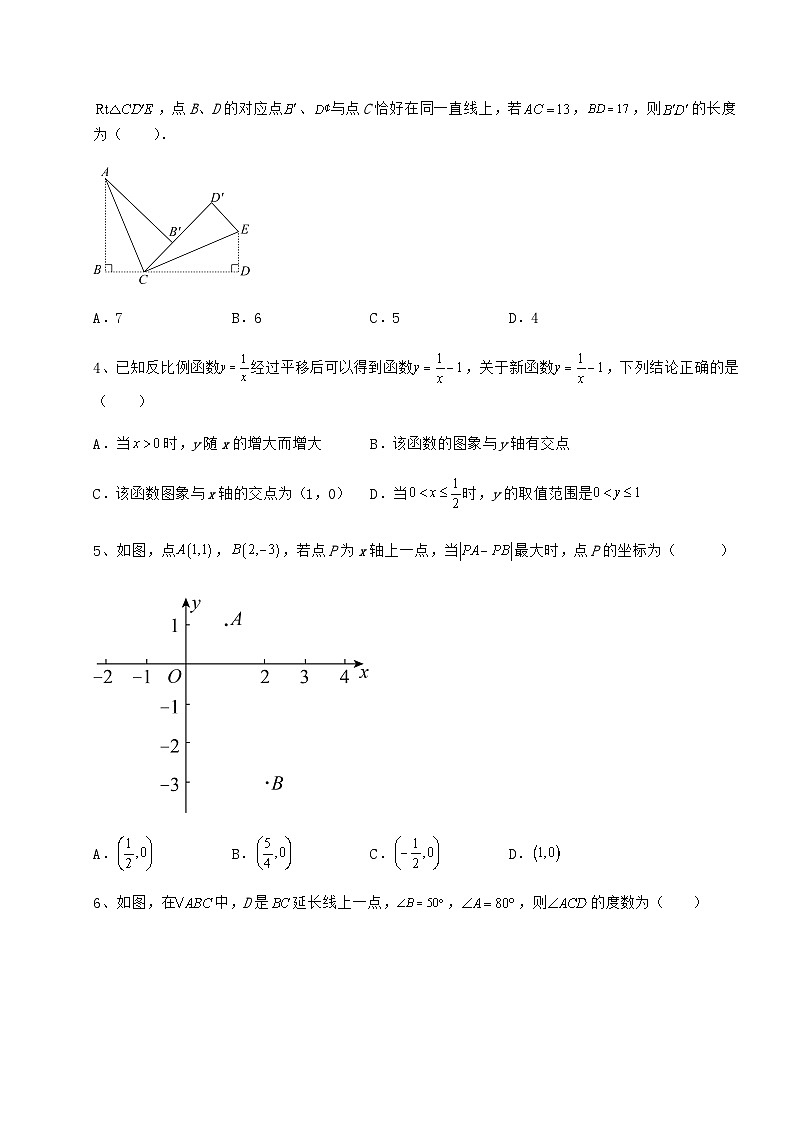
3、和按如图所示的位置摆放，顶点B、C、D在同一直线上，，，．将沿着翻折，得到，将沿着翻折，得，点B、D的对应点、与点C恰好在同一直线上，若，，则的长度为（ ）．
A．7B．6C．5D．4
4、已知反比例函数经过平移后可以得到函数，关于新函数，下列结论正确的是（ ）
A．当时，y随x的增大而增大B．该函数的图象与y轴有交点
C．该函数图象与x轴的交点为（1，0）D．当时，y的取值范围是
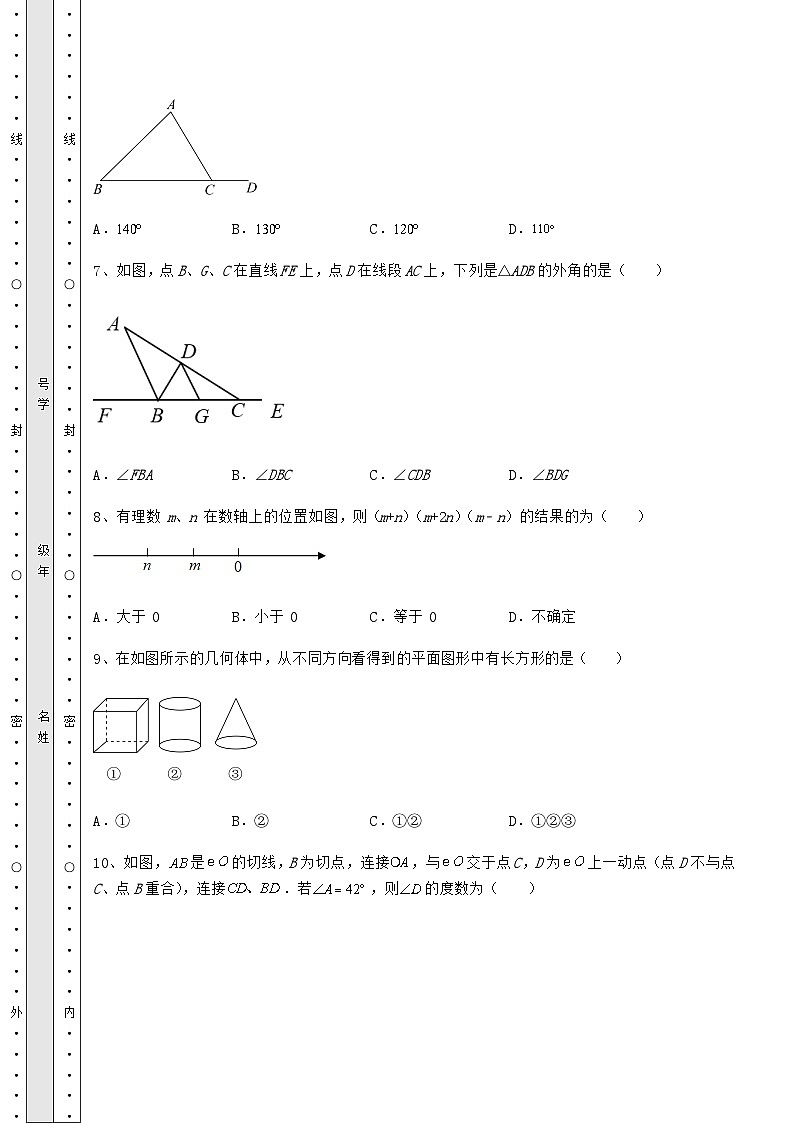
5、如图，点，，若点P为x轴上一点，当最大时，点P的坐标为（ ）
A．B．C．D．
6、如图，在中，D是延长线上一点，，，则的度数为（ ）
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
A．B．C．D．
7、如图，点B、G、C在直线FE上，点D在线段AC上，下列是△ADB的外角的是（ ）
A．∠FBAB．∠DBCC．∠CDBD．∠BDG
8、有理数 m、n 在数轴上的位置如图，则（m+n）（m+2n）（m﹣n）的结果的为（ ）
A．大于 0B．小于 0C．等于 0D．不确定
9、在如图所示的几何体中，从不同方向看得到的平面图形中有长方形的是（ ）
A．①B．②C．①②D．①②③
10、如图，是的切线，B为切点，连接，与交于点C，D为上一动点（点D不与点C、点B重合），连接．若，则的度数为（ ）
A．B．C．D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、、所表示的有理数如图所示，则________．
2、当a＝﹣1时，代数式2a2﹣a+1的值是 ___．
3、某树主干长出x根枝干，每个枝干又长出x根小分支，若主干、枝干和小分支总数共133根，则主干长出枝干的根数x为______．
4、如图，小明用一张等腰直角三角形纸片做折纸实验，其中∠C=90°，AC=BC=10，AB=10，点C关于折痕AD的对应点E恰好落在AB边上，小明在折痕AD上任取一点P，则△PEB周长的最小值是___________．
5、如图，在平面直角坐标系xOy中，P为函数图象上一点，过点P分别作x轴、y轴的垂线，垂足分别为M，N．若矩形PMON的面积为3，则m的值为______．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
三、解答题（5小题，每小题10分，共计50分）
1、已知：在四边形中，于E，且．
（1）如图1，求的度数；
（2）如图2，平分交于F，点G在上，连接，且．求证：；
（3）如图3，在（2）的条件下，，过点F作，且，若，求线段的长．
2、一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1，2，3．
（1）随机摸取一个小球的标号是奇数，该事件的概率为_______；
（2）随机摸取一个小球后放回，再随机摸取一个小球．求两次取出的小球标号相同的概率．
3、如图，在中，，．
（1）尺规作图：
①作边的垂直平分线交于点，交于点；
②连接，作的平分线交于点；（要求：保留作图痕迹，不写作法）
（2）在（1）所作的图中；求的度数．
解：∵垂直平分线段，
∴，（_________）（填推理依据）
∴，（__________）（填推理依据）
∵，∴，
∵，
∴__________，
∴__________，
∵平分，
∴__________．
4、解方程：
（1）；
（2）
5、现有面值为5元和2元的人民币共32张，币值共计100元，问：这两种人民币各有多少张？
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
-参考答案-
一、单选题
1、C
【分析】
先移项，把方程化为 再利用直接开平方的方法解方程即可.
【详解】
解：，

即
故选C
【点睛】
本题考查的是一元二次方程的解法，掌握“利用直接开平方的方法解一元二次方程”是解本题的关键.
2、A
【分析】
整个图形为一个正方形，找到边长，表示出面积；也可用1个小正方形的面积加上4个矩形的面积表示，然后让这两个面积相等即可．
【详解】
∵大正方形边长为：，面积为：；
1个小正方形的面积加上4个矩形的面积和为：；
∴．
故选：A．
【点睛】
此题考查了完全平方公式的几何意义，用不同的方法表示相应的面积是解题的关键．
3、A
【分析】
由折叠的性质得，，故，，推出，由，推出，根据AAS证明，即可得，，设，则，由勾股定理即可求出、，由计算即可得出答案．
【详解】
由折叠的性质得，，
∴，，
∴，
∵，
∴，
∴，
在与中，
，
∴，
∴，，
设，则，
∴，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
解得：，
∴，，
∴．
故选：A．
【点睛】
本题考查折叠的性质以及全等三角形的判定与性质，掌握全等三角形的判定定理和性质是解题的关键．
4、C
【分析】
函数的图象是由函数的图象向下平移1个单位长度后得到的，根据两个函数的图像，可排除A，B，C选项，将y=0代入函数可得到函数与x轴交点坐标为（1,0），故C选项正确．
【详解】
解：函数与函数的图象如下图所示：
函数的图象是由函数的图象向下平移1个单位长度后得到的，
A、由图象可知函数，当时，y随x的增大而减小，选项说法错误，与题意不符；
B、函数的图象是由函数的图象向下平移一个单位后得到的，所以函数与y轴无交点，选项说法错误，与题意不符；
C、将y=0代入函数中得，，解得，故函数与x轴交点坐标为（1,0），选项说法正确，与题意相符；
D、当时， ，有图像可知当时，y的取值范围是，故选项说法错误，与题意不符；
故选：C．
【点睛】
本题考查反比例函数的图象，以及函数图象的平移，函数与数轴的交点求法，能够画出图象，并掌握数形结合的方法是解决本题的关键．
5、A
【分析】
作点A关于x轴的对称点，连接并延长交x轴于P，根据三角形任意两边之差小于第三边可知，此时的最大，利用待定系数法求出直线的函数表达式并求出与x轴的交点坐标即可．
【详解】
解：如图，作点A关于x轴的对称点，则PA=，
∴≤（当P、、B共线时取等号），
连接并延长交x轴于P，此时的最大，且点的坐标为（1，－1），
设直线的函数表达式为y=kx+b，
将（1，－1）、B（2，－3）代入，得：
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
，解得：，
∴y=－2x+1，
当y=0时，由0=－2x+1得：x=，
∴点P坐标为（，0），
故选：A
【点睛】本题考查坐标与图形变换=轴对称、三角形的三边关系、待定系数法求一次函数的解析式、一次函数与x轴的交点问题，熟练掌握用三角形三边关系解决最值问题是解答的关键．
6、B
【分析】
根据三角形外角的性质可直接进行求解．
【详解】
解：∵，，
∴；
故选B．
【点睛】
本题主要考查三角形外角的性质，熟练掌握三角形外角的性质是解题的关键．
7、C
【分析】
根据三角形的外角的概念解答即可．
【详解】
解：A.∠FBA是△ABC的外角，故不符合题意；
B. ∠DBC不是任何三角形的外角，故不符合题意；
C.∠CDB是∠ADB的外角，符合题意；
D. ∠BDG不是任何三角形的外角，故不符合题意；
故选：C．
【点睛】
本题考查的是三角形的外角的概念，三角形的一边与另一边的延长线组成的角，叫做三角形的外角．
8、A
【分析】
从数轴上看出，判断出，进而判断的正负．
【详解】
解：由题意知：
∴
∴
故选A．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【点睛】
本题考查了有理数加减的代数式正负的判断．解题的关键在于正确判断各代数式的正负．
9、C
【分析】
分别找出每个图形从三个方向看所得到的图形即可得到答案．
【详解】
①正方体从上面、正面、左侧三个不同方向看到的形状都是正方形，符合要求；
②圆柱从左面和正面看都是长方形，从上边看是圆，符合要求；
③圆锥，从左边看是三角形，从正面看是三角形，从上面看是圆，不符合要求；故选：C．
【点睛】
本题考查了从不同方向看几何体，掌握定义是关键．注意正方形是特殊的长方形．
10、B
【分析】
如图：连接OB，由切线的性质可得∠OBA=90°，再根据直角三角形两锐角互余求得∠COB，然后再根据圆周角定理解答即可．
【详解】
解：如图：连接OB，
∵是的切线，B为切点
∴∠OBA=90°
∵
∴∠COB=90°-42°=48°
∴=∠COB=24°．
故选B．
【点睛】
本题主要考查了切线的性质、圆周角定理等知识点，掌握圆周角等于对应圆心角的一半成为解答本题的关键．
二、填空题
1、
【解析】
【分析】
根据数轴确定，得出，然后化去绝对值符号，去括号合并同类项即可．
【详解】
解：根据数轴得，
∴，
∴．
故答案为：．
【点睛】
本题考查数轴上点表示数，化简绝对值，整式加减运算，掌握数轴上点表示数，化简绝对值，整式加减运算，关键是利用数轴得出．
2、4
【解析】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
【分析】
把a=-1直接代入2a2-a+1计算即可．
【详解】
解：把a=-1代入2a2-a+1得
2a2-a+1
=2×（-1）2-（-1）+1
=2+1+1
=4；
故答案为：4．
【点睛】
本题考查了代数式的求值，掌握用数值代替代数式里的字母进行计算，正确计算结果是解题关键．
3、
【解析】
【分析】
某树主干长出x根枝干，每个枝干又长出x根小分支，则小分支有根，可得主干、枝干和小分支总数为根，再列方程解方程，从而可得答案.
【详解】
解：某树主干长出x根枝干，每个枝干又长出x根小分支，则



解得：
经检验：不符合题意；取
答：主干长出枝干的根数x为
故答案为：
【点睛】
本题考查的是一元二次方程的应用，理解题意，用含的代数式表示主干、枝干和小分支总数是解本题的关键.
4、
【解析】
【分析】
连接CE，根据折叠和等腰三角形性质得出当P和D重合时，PE+BP的值最小，即可此时△BPE的周长最小，最小值是BE+PE+PB=BE+CD+DB=BC+BE，先求出BC和BE长，代入求出即可．
【详解】
解：连接CE，
∵沿AD折叠C和E重合，
∴∠ACD=∠AED=90°，AC=AE=10，∠CAD=∠EAD，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴BE=10-10，AD垂直平分CE，即C和E关于AD对称，CD=DE，
∴当P和D重合时，PE+BP的值最小，即此时△BPE的周长最小，最小值是BE+PE+PB=BE+CD+DB=BC+BE，
∴△PEB的周长的最小值是BC+BE=10+10-10=10．
故答案为：10．
【点睛】
本题考查了折叠性质，等腰三角形性质，轴对称-最短路线问题，关键是求出P点的位置．
5、3
【解析】
【分析】
根据反比例函数的解析式是，设点，根据已知得出，即，求出即可．
【详解】
解：设反比例函数的解析式是，
设点是反比例函数图象上一点，
矩形的面积为3，
，
即，
故答案为：3．
【点睛】
本题考查了矩形的面积和反比例函数的有关内容的应用，解题的关键是主要考查学生的理解能力和运用知识点解题的能力．
三、解答题
1、
（1）120°；
（2）见解析；
（3）3．
【分析】
（1）取AD的中点F，连接EF，证明△AEF是等边三角形，进而求得∠B；
（2）作FM⊥BC于M，FN⊥AB于点N，先证明Rt△BFM≌Rt△BFN，再证明Rt△FMG≌Rt△FNA；
（3）连接AG，DF，DG，作FM⊥BC于M，先证明AF=GF=DF，从而得出∠AGH=∠AFD＝30°，进而得出∠DGC=∠DFC=120°，从而得出点G、C、D、F共圆，进而得出CA平分∠BCD，接着可证Rt△FMG≌Rt△FHD，△MCF≌△HCF，进而求得GM=CG=DH=，从而得出BM的值，进而求得BF．
（1）
解：如图1，取AD的中点F，连接EF，
∵DE⊥AC，
∴∠AED=90°，
∴AD=2AF=2EF，
∵AD=2AE，
∴AE=EF=AF，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∴∠CAD=60°，
∵∠B+∠CAD=180°，
∴∠B=120°；
（2）
证明：如图2，作FM⊥BC于M，FN⊥AB于点N，
∴∠BMF=∠BNF=90°，∠GMF=∠ANF=90°，
∵BF平分∠ABC，
∴FM=FN，
在Rt△BFM和Rt△BFN中，
，
∴Rt△BFM≌Rt△BFN（HL），
∴BM=BN，
在Rt△FMG和Rt△FNA中，
，
∴Rt△FMG≌Rt△FNA（HL），
∴MG=NA，
∴BN+NA=BM+MG，
∴AB=BG．
（3）
如图3，
连接AG，DF，DG，作FM⊥BC于M，延长GF交AD于N，
∵AF=AD，∠DAE=60°，
∴△ADF是等边三角形，
∴∠AFD=60°，AF=DF，
∵GF=AF，∠DFC=180°-∠AFD=120°，
∴AF=GF=DF，
∴∠FGD=∠FDG，∠FAG=∠FGA，
∴∠AGD=∠AFN+∠DFN=∠AFD=×60°＝30°，
∵∠ADC=120°，AD=DG，
∴∠DGA=∠DAG==30°，
∴∠DGC=180°-∠DGA-∠AGD=180°-30°-30°=120°，
∴∠DGC=∠DFC，
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
∵∠1=∠2，
∴180°-∠DGC-∠1=180°-∠DFC-∠2，
∴∠GCF=∠FDG，∠DCF=∠FGD，
∴∠GCF=∠DCF，
∵FH⊥CD，
∴FM=FH，
∵∠FMG=∠FHD=90°，
∴Rt△FMG≌Rt△FHD（HL），
∴DH=MG，
同理可得：△MCF≌△HCF（HL），
∴CM=CH=2CG，
∴GM=CG=DH，
∴3CG=CD=，
∴GM=CG=，
∴BM=BG-GM=AB-GM=5-=，
在Rt△BFM中，∠BFM=90°-∠FBM=90°-60°=30°，
∴BF=2BM=3．
【点睛】
本题考查了等边三角形的判定和性质，全等三角形的判定和性质，角平分线的性质等知识，解决问题的关键是正确作出辅助线．
2、
（1）
（2）（两次取出的小球标号相同）
【分析】
（1）直接由概率公式求解即可；
（2）画树状图，共有9种等可能的结果，两次取出小球标号相同的结果有3种，再由概率公式求解即可．
（1）
∵在1，2，3三个数中，其中奇数有1，3共2个数，
∴随机摸取一个小球的标号是奇数，该事件的概率为
故答案为：；
（2）
画树状图如下：
由树状图可知，随机摸取一个小球后放回，再随机摸取一个小球，共有9种等可能的结果，其中两次取出的小球标号相同的结果共有3种，
∴（两次取出的小球标号相同）.
【点睛】
此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率=所求情况数与总情况数之比．
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
3、（1）①图见解析；②图见解析；（2）线段垂直平分线上的点到这条线段两个端点的距离相等，等边对等角，110，80，40．
【分析】
（1）①根据线段垂直平分线的尺规作图即可得；
②先连接，再根据角平分线的尺规作图即可得；
（2）先根据线段垂直平分线的性质可得，再根据等腰三角形的性质可得，然后根据三角形的内角和定理可得，从而可得，最后根据角平分线的定义即可得．
【详解】
解：（1）①作边的垂直平分线交于点，交于点如图所示：
②连接，作的平分线交于点如图所示：
（2）∵垂直平分线段，
∴，（线段垂直平分线上的点到这条线段两个端点的距离相等）
∴，（等边对等角）
∵，
∴，
∵，
∴，
∴，
∵平分，
∴．
【点睛】
本题考查了线段垂直平分线和角平分线的尺规作图、线段垂直平分线的性质、等腰三角形的性质等知识点，熟练掌握尺规作图和线段垂直平分线的性质是解题关键．
4、
（1）x= ；
（2）x=
【分析】
（1）根据解一元一次方程的方法求解即可；
（2）根据解一元一次方程的方法求解即可．
（1）
解：去括号，得：6－9x=x+1，
移项、合并同类项，得：－10x=－5，
化系数为1，得：x= ；
（2）
解：去分母，得：2（2x+1）=6+(1－3x)，
去括号，得：4x+2=6+1－3x，
移项、合并同类项，得：7x=5，
化系数为1，得：x= ；
【点睛】
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 内 · · · · · · ○ · · · · · ·
号学级年名姓
· · · · · · 线 · · · · · · ○ · · · · · · 封 · · · · · · ○ · · · · · · 密 · · · · · · ○ · · · · · · 外 · · · · · · ○ · · · · · ·
本题考查解一元一次方程，熟练掌握一元一次方程的解法步骤是解答的关键．
5、面值为5元得人民币由12张，面值为2元得人民币由20张．
【分析】
设面值为5元得人民币由张，面值为2元得人民币由张，然后由面值共100元，列出方程，解方程即可．
【详解】
解答:解：设面值为5元得人民币由张，面值为2元得人民币由张，
根据题意得：，
解得：（张，
（张．
答：面值为5元得人民币由12张，面值为2元得人民币由20张．
【点睛】
此题属于一元一次方程的应用题，关键是由题意列出方程．