冀教版八年级下册21.1 一次函数教学演示课件ppt

这是一份冀教版八年级下册21.1 一次函数教学演示课件ppt，共16页。PPT课件主要包含了h15n，T-2t，归纳总结，②k≠0，试一试，问题探究，问题解决，∴m-1，练一练，∴m-2等内容，欢迎下载使用。
1.理解正比例函数的概念及掌握其解析式特点2.能根据问题列出函数解析式，并会识别正比例函数
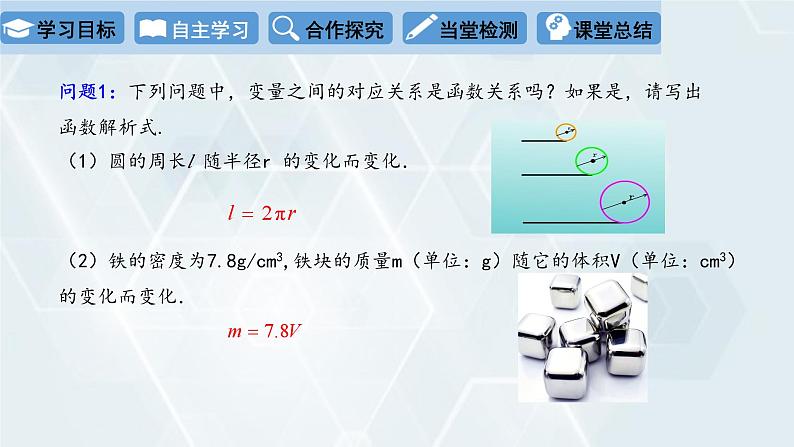
问题1：下列问题中，变量之间的对应关系是函数关系吗？如果是，请写出函数解析式.（1）圆的周长l 随半径r 的变化而变化．
（2）铁的密度为7.8g/cm3,铁块的质量m（单位：g）随它的体积V（单位：cm3）的变化而变化．
（3）每本练习本的厚度为1.5cm，一些练习本摞在一起的总厚度h（单位：cm）随练习本的本数n的变化而变化．
（4）冷冻一个0℃的物体，使它每分钟下降2℃，物体温度T（单位：℃）随冷冻时间t（单位：min）的变化而变化．
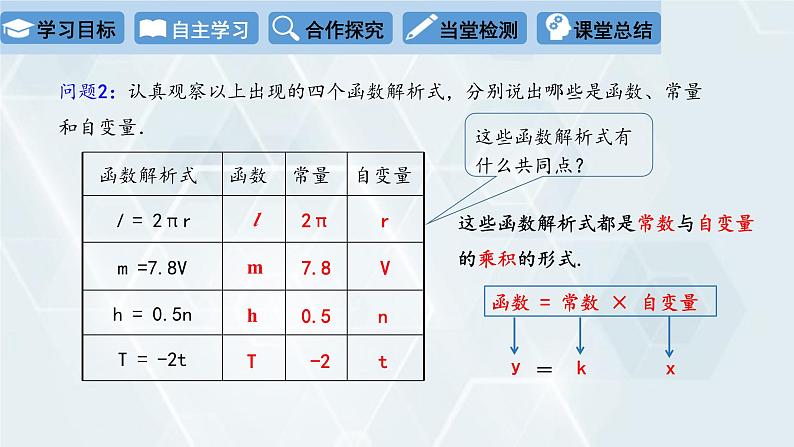
问题2：认真观察以上出现的四个函数解析式，分别说出哪些是函数、常量和自变量．
这些函数解析式有什么共同点？
这些函数解析式都是常数与自变量的乘积的形式.
函数 = 常数 × 自变量
一般地，形如y=kx（k是常数，k≠0）的函数，叫做正比例函数，其中k叫做比例系数．
注: 正比例函数y=kx(k≠0的常数)的结构特征：
③ x、y的次数是1.
①常量与自变量乘积的形式；
判断下列函数解析式是否是正比例函数？如果是，指出其比例系数是多少？
探究一 正比例函数的概念
即 m≠1，m=±1，
∴m-1≠0，m2=1，
1.正比例函数解析式有哪些特征？
(1)常量与自变量乘积的形式；
(2)常量k是不为0的常数；
(3)x、y的次数为1.
2.以上这些特征对你解题有什么启发？
m-1不为0，m2为1
即 m≠2，m=±2，
∴m-2≠0，|m|-1=1，
∴m-1≠0，m2-1=0，
探究二 正比例函数的简单应用
问题提出：已知某种小汽车的耗油量是每100km耗油15L,所使用的汽油为5元/L．（1）写出汽车行驶途中所耗油费y（元）与行程 x（km）之间的函数关系式，并指出y是x的什么函数；
1.题目中存在什么样的等量关系？
行驶途中的耗油费=行驶的路程×每行驶1km所用的汽油费
2.怎么求出每行驶1km所用的汽油费？
先根据“每100km耗油15L”求出1km耗油的量，
再根据“所使用的汽油为5元/L”求出1km耗油量需要的费用.
解：1km耗的油量为：
每1km的油量所需费用为：
∴汽车行驶途中所耗油费y(元)与行程x(km)之间的函数关系式为：
根据正比例函数的定义可知：
问题提出：已知某种小汽车的耗油量是每100km耗油15L,所使用的汽油为5元/L．（2）计算该汽车行驶220 km所需油费是多少？
该汽车行驶220 km是上述关系式中的哪个未知数？
答：该汽车行驶220 km所需油费为165元．
2.列式表示下列问题中y与x的函数关系，并指出哪些是正比例函数．（1）正方形的边长为x cm，周长为y cm.（2）某人一年内的月平均收入为x元，他这年（12个月）的总收入为y元．（3）一个长方体的长为2 cm，宽为1.5 cm，高为x cm ，体积为y cm3.
(2)y=12x，
(3)y=2×1.5x
1.下列说法正确的打“√”，错误的打“×”. （1）若y=kx，则y是x的正比例函数 （ ） （2）若y=2x2，则y是x的正比例函数 （ ） （3）若y=2(x-1)+2，则y是x的正比例函数 （ ） （4）若y=(2+k2)x，则y是x的正比例函数 （ ）
注意：（1）中k可能为0；
（4）中2+k2＞0，故y是x的正比例函数.
2.有一块10公顷的成熟麦田，用一台收割速度为0.5公顷每小时的小麦收割机来收割.（1）求收割的面积y（单位：公顷）与收割时间x（单位：时）之间的函数关系式，并指出y是x的什么函数；
（2）求收割完这块麦田需用的时间.
答：收割完这块麦田需用20小时.