初中数学冀教版八年级下册22.4 矩形图片课件ppt

这是一份初中数学冀教版八年级下册22.4 矩形图片课件ppt，共18页。PPT课件主要包含了判定定理，逆命题，矩形的判定定理1，矩形的判定定理2，问题探究，问题解决，又∵OAOD，∴ACBD，∴∠BAD90°，∴∠OAB40°等内容，欢迎下载使用。
1.会用矩形的定义来判定一个四边形为矩形.2.掌握矩形的判定定理,会证明一个四边形为矩形.3.能解决与矩形相关的几何问题.
工人师傅在做门窗或矩形零件时，如何确保图形是矩形呢？现在师傅带了两种工具（卷尺和量角器），他说用这两种工具的任意一种就可以解决问题，这是为什么呢？
类比平行四边形的定义也是判定平行四边形的一种方法，那么矩形的定义也是判定矩形的一种方法.
问题1：除了定义以外，判定矩形的方法还有没有呢？
矩形是特殊的平行四边形，类似的，我们也可以参照之前研究平行四边形判定定理的方法来研究矩形的判定方法.
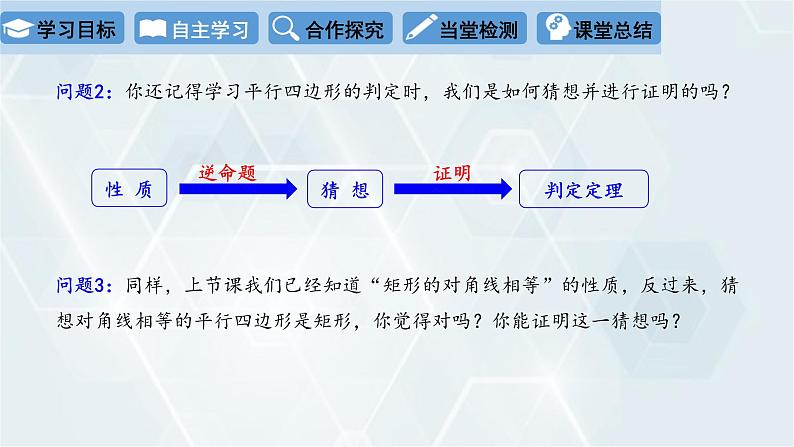
问题2：你还记得学习平行四边形的判定时，我们是如何猜想并进行证明的吗？
问题3：同样，上节课我们已经知道“矩形的对角线相等”的性质，反过来，猜想对角线相等的平行四边形是矩形，你觉得对吗？你能证明这一猜想吗？
证一证：已知：如图,在□ABCD中，AC、BD是它的两条对角线, AC=BD. 求证：□ABCD是矩形.
证明：在□ABCD中，由于AB=DC，AC=DB，BC=CB，
因此 △ABC≌△DCB. (SSS)
从而 ∠ABC=∠DCB.
又 ∠ABC +∠DCB =180°，
于是 ∠ABC=90°.
所以 □ABCD是矩形.
对角线相等的平行四边形是矩形.
问题4：上节课我们研究了矩形的四个角，知道它们都是直角，它的逆命题是什么？成立吗？
逆命题：四个角是直角的四边形是矩形.
问题5：至少有几个角是直角的四边形是矩形？
猜想：有三个角是直角的四边形是矩形.
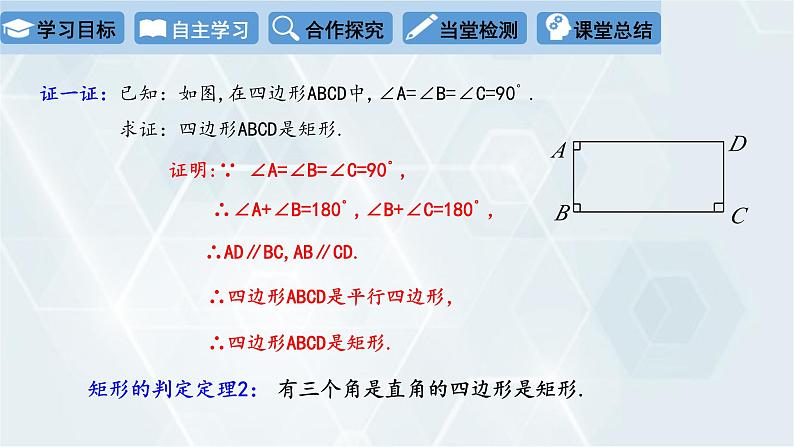
证一证：已知：如图,在四边形ABCD中,∠A=∠B=∠C=90°. 求证：四边形ABCD是矩形.
有三个角是直角的四边形是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°，
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形，
∴四边形ABCD是矩形.
探究 矩形判定定理的运用
问题提出1：如图，在□ABCD中，对角线AC，BD相交于点O，且OA=OD，∠OAD=50°．求∠OAB的度数．
(1)根据题目给出□ABCD和它的两条对角线，你能想到它的什么性质呢？
平行四边形的对角线互相平分
(2)再结合题目已知的OA=OD,我们可以得到什么结论？
可以根据矩形的判定定理1，证得矩形.
(3)最后根据已知∠OAD=50°，得出∠OAB的度数.
解：∵四边形ABCD是平行四边形，
∴四边形ABCD是矩形（对角线相等的平行四边形是矩形），
又∵∠OAD=50°，
问题提出2：如图，□ ABCD的四个内角的平分线分别相交于E、F、G、H，求证：四边形EFGH为矩形．
根据题中已知平行四边形我们可以得到关于边的关系： ，
结合平行线的性质,可知同旁内角 ,所以平行四边形两个邻角的和为 .
再观察题中给出的内角的平分线，可知这些平分线分别平分 ，
最后根据三角形的内角和度数，可分别求出四边形EFGH内角的度数，依据矩形的判定定理 即可得证.
证明：在□ ABCD中，AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、∠ABC的平分线,
∴四边形EFGH是矩形．
同理可证∠AED=∠EHG=90°（有三个角是直角的四边形是矩形）,
1.在判断“一个四边形门框是否为矩形”的数学活动课上，一个合作学习小组的4位同学分别拟定了如下的方案，其中正确的是（　　）A．测量对角线是否相等 B．测量两组对边是否分别相等 C．测量一组对角是否都为直角 D．测量其中三个角是否都为直角
2.如图，平行四边形ABCD中，对角线AC、BD相交于点O，延长OA到N，使ON＝OB，再延长OC至M，使CM＝AN.求证：四边形NDMB为矩形．
证明：∵四边形ABCD为平行四边形，
∴AO＝OC，OD＝OB.
∵AN＝CM，ON＝OB，
∴ON＝OM＝OD＝OB，
∴四边形NDMB为平行四边形，MN＝BD，
∴平行四边形NDMB为矩形．
3.如图，在四边形ABCD中，AB∥CD，∠BAD=90°，AB=5，BC=12，AC=13．求证：四边形ABCD是矩形．
证明：四边形ABCD中，AB∥CD，∠BAD=90°，
又∵△ABC中，AB=5，BC=12，AC=13，
满足132=52+122，即AB2+BC2=AC2,
∴△ABC是直角三角形，且∠B=90°，
∴四边形ABCD是矩形．
4.如图，在平行四边形ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG=AE，连接CG．（1）求证：△ABE≌△CDF；
证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，OB=OD，OA=OC，
∴∠ABE=∠CDF，
∵点E，F分别为OB，OD的中点，
在△ABE和△CDF中，
∴△ABE≌△CDF（SAS）；
（2）当线段AB与线段AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．
解：当AC=2AB时，四边形EGCF是矩形；理由如下：
∵AC=2OA，AC=2AB，
∵EG=AE，OA=OC，
∴OE是△ACG的中位线，
∴四边形EGCF是平行四边形,
∴四边形EGCF是矩形．