初中数学冀教版八年级下册 课件 第二十二章 复习课

这是一份初中数学冀教版八年级下册 课件 第二十二章 复习课，共25页。

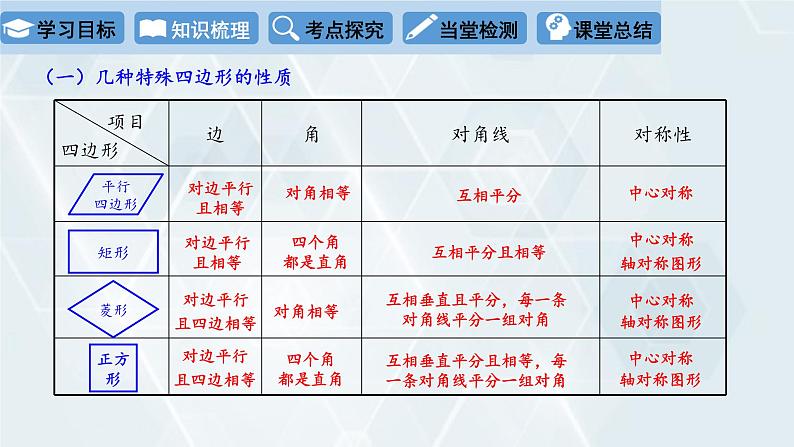
复习课第二十二章 四边形1.梳理掌握平行四边形、矩形、菱形、正方形的性质和判定2.进一步巩固三角形中位线的性质，能灵活运用性质解题3.会用多边形内角和定理、外角和定理解决问题（一）几种特殊四边形的性质平行四边形矩形菱形正方形对边平行且相等对角相等互相平分对边平行且相等四个角都是直角互相平分且相等中心对称轴对称图形对边平行且四边相等对角相等互相垂直且平分，每一条对角线平分一组对角中心对称轴对称图形对边平行且四边相等四个角都是直角互相垂直平分且相等，每一条对角线平分一组对角中心对称轴对称图形中心对称（二）几种特殊四边形的常用判定方法1.定义：两组对边分别平行；1.定义：有一个角是直角的平行四边形；1.定义：一组邻边相等的平行四边形;1.有一组邻边相等的矩形；2.两组对边分别相等；3.两组对角分别相等； 4.对角线互相平分； 5.一组对边平行且相等. 2.对角线相等的平行四边形；3.有三个角是直角的四边形.2.对角线互相垂直的平行四边形；3.四条边都相等的四边形.2.有一个角是直角的菱形.（三）其他重要概念及性质1.三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半.（四）多边形的内角和与外角和(2)多边形内角的 与另一边的 组成的角叫做这个多边形的外角；在每个顶点处取一个外角，它们的和叫做这个多边形的 ．(3)任意多边形的外角和等于外角和是 . (1)n边形的内角和是 .(n-2)·180°一边反向延长线外角和360°考点一 平行四边形的性质与判定 例1.如图，在直角梯形ABCD中，AD∥BC，∠B＝90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG.(1)求证：四边形DEGF是平行四边形；证明：∵AG∥DC，AD∥BC，∴四边形AGCD是平行四边形，∴AG＝DC.∵E、F分别为AG、DC的中点，即GE＝DF，GE∥DF，∴四边形DEGF是平行四边形（一组对边平行且相等的四边形是平行四边形）.考点一 平行四边形的性质与判定 (2)如果点G是BC的中点，且BC＝12，DC＝10，求四边形AGCD的面积．解：∵点G是BC的中点，BC＝12，∵四边形AGCD是平行四边形，AG＝DC＝10，在Rt△ABG中，根据勾股定理得AB＝8，∴四边形AGCD的面积为:CG·AB=6×8＝48.方法总结：涉及判定平行四边形(或边角关系的证明)，注意灵活使用平行四边形的性质及判定方法，必要时借助判定三角形全等等方法来证明.1.下列能判定四边形ABCD是平行四边形的有 . ① AB = CD，AD = BC; ② AB∥CD，AB = CD; ③ AD∥BC，AB = CD; ④ AB∥CD，AD∥BC;⑤∠A=∠C，∠B=∠D. ①②④⑤ 2.如图，在四边形ABCD中，AB=CD，∠BAC=∠DCA．（1）求证：四边形ABCD为平行四边形．（2）若AC=4，CD=5，AC⊥BC，求BD的长．（1）证明：∵∠BAC=∠DCA，∴AB∥CD，又∵AB=CD，∴四边形ABCD为平行四边形；（2）∵四边形ABCD为平行四边形，∴AE=EC=2，BE=DE，AB=CD=5，∵AC⊥BC，解析：∵在△ABC中，点E、F分别是AC，BC的中点，∵EF=5cm，∴AB=10cm；10考点二 三角形的中位线的性质及应用 ∴EF是△ABC的中位线，中线AF与中位线DE互相平分.（2）中线AF与中位线DE有什么特殊的关系？证明你的猜想.∴四边形ADFE是平行四边形，AF、DE为对角线，理由：连接DF，∴中线AF与中位线DE互相平分.考点二 三角形的中位线的性质及应用 证明：E，F分别是BD，CD的中点，∴EF∥BC，∵AB=AD，∴∠ABD=∠ADB，∵BD平分∠ABC，∴∠ABD=∠DBC，∴∠ADB=∠DBC，∴AD∥BC，又EF∥BC，∴AD∥EF.考点三 特殊平行四边形的性质与判定 例3.如图，在Rt△ABC中，∠ABC=90°，BO为斜边AC上的中线，延长BO至点D，使OD=OB，连接AD、CD.补全图形，并证明四边形ABCD是矩形．分析：首先根据题目要求作图，然后利用对角线互相平分证得四边形ABCD是平行四边形，最后利用对角线相等证得为矩形．例3.如图，在Rt△ABC中，∠ABC=90°，BO为斜边AC上的中线，延长BO至点D，使OD=OB，连接AD、CD.补全图形，并证明四边形ABCD是矩形． ∵Rt△ABC中，BO为斜边的中线，∴AO=CO=BO(直角三角形斜边上的中线等于斜边的一半)，∵BO=OD，∴AO=CO=BO=DO，∴四边形ABCD为平行四边形，∵AC=DB，∴四边形ABCD为矩形(对角线相等的平行四边形是矩形)．D考点三 特殊平行四边形的性质与判定 解：如右图所示，考点三 特殊平行四边形的性质与判定 例4.如图，已知在四边形ABFC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D，交AB于点E，且CF＝AE；(1)试判断四边形BECF是什么四边形？并说明理由；解：四边形BECF是菱形．理由如下：∵EF垂直平分BC，∴BF＝FC，BE＝EC，∴∠3＝∠1.∵∠ACB＝90°，∴∠3＋∠4＝90°，∠1＋∠2＝90°,∴∠2＝∠4，∴EC＝AE，∵CF＝AE，∴BE＝EC＝CF＝BF，∴四边形BECF是菱形.考点三 特殊平行四边形的性质与判定 (2)当∠A的大小满足什么条件时，四边形BECF是正方形？请回答并证明你的结论．当∠A＝45°时，菱形BECF是正方形．证明如下：∵∠A＝45°，∠ACB＝90°，∴∠3＝45°，∵菱形BECF中∠EBF＝2∠3＝90°，∴菱形BECF是正方形(有一个角是直角的菱形是正方形)．4.如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处，（1）求证：△ABE≌△GAF；证明：∵四边形ABC是平行四边形，∴AB=CD，∠BAD=∠BCD，∠B=∠D，根据折叠的性质，可得AG=CD，∠EAG=∠BCD，∴AB=AG，∠BAD=∠EAG，∴∠BAE=∠GAF，∵AB∥CD，AE∥GF，AD∥BC，∴∠BEA=∠EAF=∠GFA，∴△ABE≌△GAF.4.如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处，（2）连接CF.判定四边形AECF是什么四边形，并证明你的结论.解：四边形AECF是菱形，∵AD∥BC，AE∥CF，∴四边形AECF是平行四边形，又∵AE=EC，∴四边形AECF是菱形.5.如图，在菱形ABCD中，对角线AC与BD交于点O，过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E，判断四边形OCED的形状，并说明理由．解：平行四边形OCED是矩形，理由如下：∵四边形ABCD是菱形，∴AC⊥BD，∴∠COD=90°．∵CE∥OD，DE∥OC，∴四边形OCED是平行四边形，又∠COD=90°，∴平行四边形OCED是矩形.考点四 多边形的内角和与外角和例5.已知一个多边形的每个内角都是其相邻外角度数的4倍，求这个多边形的边数. 解：设此多边形的外角的度数为 x，则内角的度数为 4x，解得：x = 36°，因为多边形的外角和为360°，所以边数 n = 360°÷ 36°= 10 .故这个多边形为 10 边形.则 x + 4x = 180°，分析：根据题意列出内外角关系式，算出外角的度数，再算出边数即可.方法总结 ：(1)在多边形的有关求边数或内角、外角度数的问题中，要注意内角与外角之间的转化，以及内角和、外角和定理的运用；(2)在求边数的问题中，常常利用内角和、对角线的规律、外角和定理等列出方程，再求得边数.6.从多边形的一个顶点可以画7条对角线，则这个n边形的内角和为（ ）A. 1620° B. 1800° C. 900° D. 1440°点拨：从多边形的一个顶点可引出(n-3)条对角线. D7.(1)多边形的边数每增加一条，那么它的内角和就增加 .(2)一个多边形的内角和等于外角和的3倍，则这个多边形的边数是 ． 8180°