物理必修 第二册2 运动的合成与分解课后作业题

这是一份物理必修 第二册2 运动的合成与分解课后作业题，共26页。

一、一个平面运动的实例
1．实验观察蜡块的运动
蜡块在竖直玻璃管内向上匀速运动的同时，将玻璃管沿水平方向向右做匀速运动，观察到蜡块向右上方运动。
2．蜡块的位置：蜡块沿玻璃管匀速上升的速度设为vy，玻璃管向右匀速移动的速度设为vx。从蜡块开始运动的时刻计时，于是，在时刻t，蜡块的位置P可以用它的x、y两个坐标表示x＝vxt，y＝vyt。
3．蜡块运动的轨迹
由以上两式消去t，得y＝eq \f(vy,vx)x，由于vx和vy均是常量，所以蜡块运动的轨迹是一条过原点的直线。y＝eq \f(vy,vx)x为轨迹方程。
4．蜡块的速度
由勾股定理可得：v＝eq \r(v\\al(2,x)＋v\\al(2,y))，v与x轴正方向间夹角的正切为tanθ＝eq \f(vy,vx)。
二、运动的合成与分解
1．合运动与分运动：一个物体同时参与几个运动，那么物体实际发生的运动叫做合运动，参与的那几个运动叫做分运动。
2．运动的合成与分解
(1)运动的合成：由已知的分运动求合运动的过程。
(2)运动的分解：由已知的合运动求分运动的过程。
(3)运算法则：运动的合成与分解遵从矢量运算法则。
【方法突破】
一、对运动的合成与分解的理解
■方法归纳
1．合运动与分运动的关系
2．运动的合成与分解法则
运动的合成与分解是指描述物体运动的各物理量即位移、速度、加速度的合成与分解．由于它们都是矢量，所以它们都遵循矢量的合成与分解法则．
①两分运动在同一直线上时，同向相加，反向相减．
②不在同一直线上，按照平行四边形定则进行合成或分解．
3．合运动与分运动的性质和轨迹的关系：两直线运动的合运动的性质和轨迹，由各分运动性质及合初速度与合加速度的方向和大小关系决定．
①两个匀速直线运动的合运动一定是匀速直线运动．
②一个匀速直线运动和一个匀变速直线运动的合运动是匀变速运动，当二者共线时为匀变速直线运动，不共线时为匀变速曲线运动．
③两个匀变速直线运动的合运动一定是匀变速运动．若合初速度方向与合加速度方向在同一条直线上，则是直线运动；若合初速度方向与合加速度方向不在一条直线上，则是曲线运动．
【例1】如图甲所示，在一端封闭、长约1m的玻璃管中注满清水，水中放一个直径略小于玻璃管内径的圆柱形红蜡块R，将玻璃管的开口端用胶塞塞紧。把玻璃管迅速竖直倒置，红蜡块R就沿玻璃管由管口A匀速上升，在红蜡块刚从管口A开始匀速上升的同时，将玻璃管由静止开始水平向右匀加速移动（如图乙所示），直至红蜡块上升到管底B的位置（如图丙所示）。以地面为参考系，以红蜡块开始匀速运动的位置为原点，以水平向右为x轴正方向，竖直向上为y轴正方向建立平面直角坐标系，描绘红蜡块R在这一运动过程中的轨迹，图中可能正确的是（ ）
A．B．C．D．
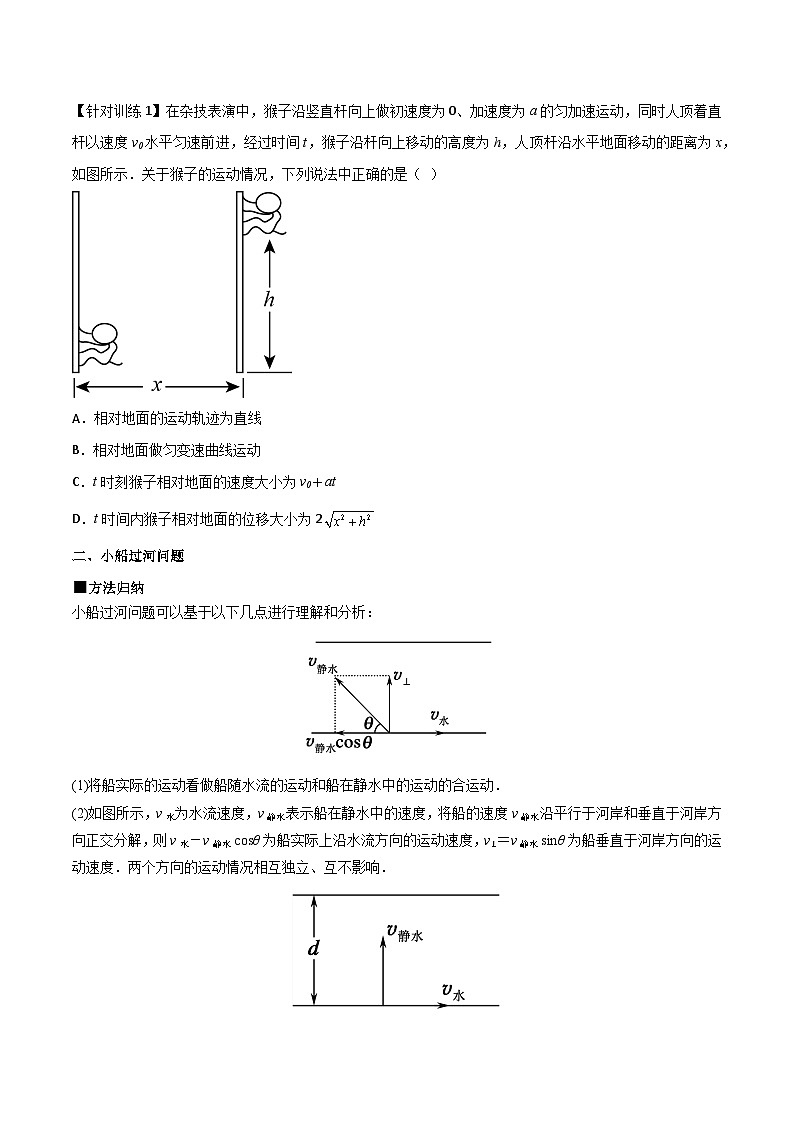
【针对训练1】在杂技表演中，猴子沿竖直杆向上做初速度为0、加速度为a的匀加速运动，同时人顶着直杆以速度v0水平匀速前进，经过时间t，猴子沿杆向上移动的高度为h，人顶杆沿水平地面移动的距离为x，如图所示．关于猴子的运动情况，下列说法中正确的是（ ）
A．相对地面的运动轨迹为直线
B．相对地面做匀变速曲线运动
C．t时刻猴子相对地面的速度大小为v0＋at
D．t时间内猴子相对地面的位移大小为2
二、小船过河问题
■方法归纳
小船过河问题可以基于以下几点进行理解和分析：
(1)将船实际的运动看做船随水流的运动和船在静水中的运动的合运动．
(2)如图所示，v水为水流速度，v静水表示船在静水中的速度，将船的速度v静水沿平行于河岸和垂直于河岸方向正交分解，则v水－v静水csθ为船实际上沿水流方向的运动速度，v⊥＝v静水sinθ为船垂直于河岸方向的运动速度．两个方向的运动情况相互独立、互不影响．
1．过河的最短时间
过河时间仅由v静水垂直于河岸的分量v⊥决定，即t＝eq \f(d,v⊥)，与v水无关．要使过河时间最短，应使垂直河岸方向的速度最大，如图所示，当sinθ＝1，即v静水垂直于河岸时，过河所用时间最短，最短时间为t＝eq \f(d,v静水)，与v水无关．
2．过河的最小位移
过河位移由实际运动轨迹的方向决定，要使过河位移最小，应使合位移(或合速度)与河岸方向的夹角最大．
(1)当v水(2)当v水>v静水时，不论船的航向如何，总是被水冲向下游．此时合速度v与河岸方向的夹角α越大，船过河的位移越小．那么，在什么条件下α角最大呢？如图所示，以v水的矢尖为圆心，以v静水的大小为半径画圆，当合速度与圆相切时，α角最大．由三角形的相似性，最小位移为s＝eq \f(v水,v静水)d，过河时间t＝eq \f(s,v)＝eq \f(v水d,v静水\r(v\\al(2,水)－v\\al(2,静水))) .
【例2】如图所示，一条小船渡河，河水流速，船在静水中速度，船头方向与河岸垂直。关于小船的运动，下列说法正确的是（ ）
A．小船的实际运动轨迹与岸垂直
B．此时小船的渡河时间不是最短
C．小船相对于岸的速度大小为
D．小船相对于岸的速度大小为
【针对训练2】如图所示，河水流速以及渡船在静水中的划行速度大小均恒定，渡船从平直河岸边的A处开始渡河，当船头方向垂直河岸时，渡船到达正对岸岸边B处下游的C处，A、C连线与水流方向的夹角为60°。若要使渡船从A处开始渡河，能够沿直线到达B处，则船头方向与水流反方向的夹角θ的正切值应为（ ）
A．B．C．D．
三、关联速度问题
■方法归纳
绳、杆关联问题是指物拉绳(杆)或绳(杆)拉物问题．高中阶段研究的绳都是不可伸长的，杆都是不可伸长和不可压缩的，即绳或杆的长度不会改变，所以解题的原则是：把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相等求解．常见的模型如图所示．

【例3】如题图所示，汽车通过绳子绕过定滑轮连接重物M一起运动，不计滑轮摩擦和绳子质量，已知重物M以v匀速向上运动，连接汽车的轻绳与水平方向夹角为θ，汽车的速度用v汽表示。则（ ）
A．B．
C．汽车做匀速运动D．汽车做匀加速运动
【针对训练3】A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体B以的速度向左匀速运动，如图所示，当绳被拉成与水平面夹角分别是、时。物体A的运动速度为（绳始终有拉力）（ ）
A．B．C．D．
【巩固提升】
1．质量为2kg的质点在xOy平面上做曲线运动，在x方向的速度图像和y方向的位移图像如图所示，下列说法中正确的是（ ）
A．质点的初速度大小为3m/s
B．质点所受的合外力为3N，做匀变速曲线运动
C．2s内质点的位移大小约为17m
D．2s末质点速度大小为6m/s
2．在我校某周年校庆活动上，一小型无人机在空中航拍，将其运动沿水平方向和竖直方向分解，水平位移x随时间t变化的图像如图甲所示，竖直方向的速度随时间变化的图像如图乙所示。关于无人机的运动，下列说法正确的是（ ）
A．内做匀加速曲线运动B．时速度大小为
C．内加速度大小为D．内位移大小为
3．物体在直角坐标系xOy所在的平面内由O点开始运动，x轴方向的加速度随时间变化图像如图a所示，y轴方向速度随时间变化的图像如图b所示，物体的初速度为2m/s，则对该物体运动过程的描述正确的是（ ）
A．物体在0～2s做直线运动，在2s～3s做曲线运动
B．物体在0～2s的加速度大小为，2s～3s的加速度大小为
C．物体在0～2s和2s～3s内位移之比为
D．物体2s末速度最大，最大值为
4．民族运动会上有一直线侧向骑射项目如图所示，运动员骑在沿直线奔跑的马上，弯弓放箭射击跑道外侧的固定目标，假设运动员骑马奔驰的速度为v1，运动员静止时射出的弓箭速度为v2，跑道距离固定目标的最近距离为d，要想命中目标且射出的箭在空中飞行时间最短（不考虑空气阻力的影响），则（ ）
A．运动员放箭处离目标的距离为
B．运动员放箭处离目标的距离为
C．箭射到固定目标的最短时间为
D．箭射到固定目标的最短时间为
5．唐僧、悟空、沙僧和八戒师徒四人想划船渡过一条宽150m的河，他们在静水中划船的速度大小为3m/s，河水的流速为5m/s，对于这次划船过河，他们有各自的看法，其中正确的是（ ）
A．唐僧说：我们要想到达正对岸就得朝着正对岸划船，最短时间需要50s
B．悟空说：我们要想节省时间就得朝着正对岸划船，最短时间需要30s
C．沙僧说：我们要想少走点路就得朝着正对岸划船。最短路程需要150m
D．八戒说：今天这种情况我们是不可能到达正对岸的，渡河最短路程需要250m
6．如图，阿玮要渡过湍急的河水游到河对岸去，已知水流的速度是2m/s，阿玮游泳的速度是1m/s，岸宽30m，阿玮想尽量不被水冲得太远，则到达对岸时，偏离正对岸的最小距离为（ ）
A．30mB．C．D．60m
7．一条船要在最短时间内渡过宽为100m的河，已知河水的流速与船离河岸的距离变化的关系如图甲所示，船在静水中的速度与时间的关系如图乙所示，则以下判断中正确的是（ ）
A．船渡河的最短时间25s
B．船运动的轨迹可能是直线
C．船在河水中航行的平均加速度大小为
D．船在河水中的最大速度是
8．如图所示，水平固定的光滑细长杆上套有一物块Q，跨过悬挂于O点的轻小光滑圆环的细线一端连接Q，另一端悬挂一物块P。设细线的左边部分与水平方向的夹角为，初始时很小，现将P、Q由静止同时释放，关于P、Q以后的运动，下列说法正确的是（ ）
A．在向90°增大的过程中，P一直处于超重状态
B．当时，P的速度最大
C．当时，Q的速度最大
D．当时，P、Q的速度大小之比是
9．如图所示，某救援队利用如下装置转运救灾物资，物资穿在竖直固定光滑杆上，若汽车速度为，物资运动速度为，定滑轮左右两侧轻绳与竖直方向夹角分别为、。不计滑轮质量以及绳与滑轮间的摩擦，下列关系正确的是（ ）
A．B．
C．D．
10．一个半径为R的半圆柱体沿水平方向向右以速度v0匀速运动，在半圆柱体上搁置一根竖直杆，此杆只能沿竖直方向运动，如图所示．当杆与半圆柱体接触点与柱心的连线与竖直方向的夹角为θ，则竖直杆运动的速度为：（ ）
A．v0sinθB．v0tanθC．v0csθD．
独立性
一个物体同时参与两个运动，其中的任一个分运动并不会因为有另外的分运动的存在而有所改变。即各分运动是互相独立的、互不影响的
等时性
各个分运动与合运动总是同时开始，同时结束，经历的时间相等。不是同时发生的运动不能进行运动的合成
等效性
各分运动合成起来和合运动效果相同，即分运动与合运动可以“等效替代”
同体性
合运动和它的分运动必须对应同一个物体的运动，一个物体的合运动不能分解为另一个物体的分运动
第2节 运动的合成与分解
【知识梳理】
一、一个平面运动的实例
1．实验观察蜡块的运动
蜡块在竖直玻璃管内向上匀速运动的同时，将玻璃管沿水平方向向右做匀速运动，观察到蜡块向右上方运动。
2．蜡块的位置：蜡块沿玻璃管匀速上升的速度设为vy，玻璃管向右匀速移动的速度设为vx。从蜡块开始运动的时刻计时，于是，在时刻t，蜡块的位置P可以用它的x、y两个坐标表示x＝vxt，y＝vyt。
3．蜡块运动的轨迹
由以上两式消去t，得y＝eq \f(vy,vx)x，由于vx和vy均是常量，所以蜡块运动的轨迹是一条过原点的直线。y＝eq \f(vy,vx)x为轨迹方程。
4．蜡块的速度
由勾股定理可得：v＝eq \r(v\\al(2,x)＋v\\al(2,y))，v与x轴正方向间夹角的正切为tanθ＝eq \f(vy,vx)。
二、运动的合成与分解
1．合运动与分运动：一个物体同时参与几个运动，那么物体实际发生的运动叫做合运动，参与的那几个运动叫做分运动。
2．运动的合成与分解
(1)运动的合成：由已知的分运动求合运动的过程。
(2)运动的分解：由已知的合运动求分运动的过程。
(3)运算法则：运动的合成与分解遵从矢量运算法则。
【方法突破】
一、对运动的合成与分解的理解
■方法归纳
1．合运动与分运动的关系
2．运动的合成与分解法则
运动的合成与分解是指描述物体运动的各物理量即位移、速度、加速度的合成与分解．由于它们都是矢量，所以它们都遵循矢量的合成与分解法则．
①两分运动在同一直线上时，同向相加，反向相减．
②不在同一直线上，按照平行四边形定则进行合成或分解．
3．合运动与分运动的性质和轨迹的关系：两直线运动的合运动的性质和轨迹，由各分运动性质及合初速度与合加速度的方向和大小关系决定．
①两个匀速直线运动的合运动一定是匀速直线运动．
②一个匀速直线运动和一个匀变速直线运动的合运动是匀变速运动，当二者共线时为匀变速直线运动，不共线时为匀变速曲线运动．
③两个匀变速直线运动的合运动一定是匀变速运动．若合初速度方向与合加速度方向在同一条直线上，则是直线运动；若合初速度方向与合加速度方向不在一条直线上，则是曲线运动．
【例1】如图甲所示，在一端封闭、长约1m的玻璃管中注满清水，水中放一个直径略小于玻璃管内径的圆柱形红蜡块R，将玻璃管的开口端用胶塞塞紧。把玻璃管迅速竖直倒置，红蜡块R就沿玻璃管由管口A匀速上升，在红蜡块刚从管口A开始匀速上升的同时，将玻璃管由静止开始水平向右匀加速移动（如图乙所示），直至红蜡块上升到管底B的位置（如图丙所示）。以地面为参考系，以红蜡块开始匀速运动的位置为原点，以水平向右为x轴正方向，竖直向上为y轴正方向建立平面直角坐标系，描绘红蜡块R在这一运动过程中的轨迹，图中可能正确的是（ ）
A．B．C．D．
【答案】C
【详解】由题意可知红蜡块竖直向上做匀速直线运动，水平向右做初速度为零的匀加速直线运动，合运动为匀变速曲线运动，其速度方向与水平方向的夹角的正切值为由上式可知θ随t的增大而逐渐减小，而蜡块速度方向沿轨迹切线方向，所以红蜡块实际运动的轨迹可能是C。故选C。
【针对训练1】在杂技表演中，猴子沿竖直杆向上做初速度为0、加速度为a的匀加速运动，同时人顶着直杆以速度v0水平匀速前进，经过时间t，猴子沿杆向上移动的高度为h，人顶杆沿水平地面移动的距离为x，如图所示．关于猴子的运动情况，下列说法中正确的是（ ）
A．相对地面的运动轨迹为直线
B．相对地面做匀变速曲线运动
C．t时刻猴子相对地面的速度大小为v0＋at
D．t时间内猴子相对地面的位移大小为2
【答案】B
【详解】A．猴子在水平方向上做匀速直线运动，竖直方向上做初速度为0的匀加速直线运动，猴子相对地面的运动轨迹为曲线，A错误；
B．因为猴子受到的合外力恒定(加速度恒定)，所以相对地面猴子做的是匀变速曲线运动，B正确；
C．t时刻猴子对地的水平速度为v0，竖直速度为at，因此和速度大小为v＝，C错误；
D．t时间内猴子对地的位移大小为s＝，D错误。故选B。
二、小船过河问题
■方法归纳
小船过河问题可以基于以下几点进行理解和分析：
(1)将船实际的运动看做船随水流的运动和船在静水中的运动的合运动．
(2)如图所示，v水为水流速度，v静水表示船在静水中的速度，将船的速度v静水沿平行于河岸和垂直于河岸方向正交分解，则v水－v静水csθ为船实际上沿水流方向的运动速度，v⊥＝v静水sinθ为船垂直于河岸方向的运动速度．两个方向的运动情况相互独立、互不影响．
1．过河的最短时间
过河时间仅由v静水垂直于河岸的分量v⊥决定，即t＝eq \f(d,v⊥)，与v水无关．要使过河时间最短，应使垂直河岸方向的速度最大，如图所示，当sinθ＝1，即v静水垂直于河岸时，过河所用时间最短，最短时间为t＝eq \f(d,v静水)，与v水无关．
2．过河的最小位移
过河位移由实际运动轨迹的方向决定，要使过河位移最小，应使合位移(或合速度)与河岸方向的夹角最大．
(1)当v水(2)当v水>v静水时，不论船的航向如何，总是被水冲向下游．此时合速度v与河岸方向的夹角α越大，船过河的位移越小．那么，在什么条件下α角最大呢？如图所示，以v水的矢尖为圆心，以v静水的大小为半径画圆，当合速度与圆相切时，α角最大．由三角形的相似性，最小位移为s＝eq \f(v水,v静水)d，过河时间t＝eq \f(s,v)＝eq \f(v水d,v静水\r(v\\al(2,水)－v\\al(2,静水))) .
【例2】如图所示，一条小船渡河，河水流速，船在静水中速度，船头方向与河岸垂直。关于小船的运动，下列说法正确的是（ ）
A．小船的实际运动轨迹与岸垂直
B．此时小船的渡河时间不是最短
C．小船相对于岸的速度大小为
D．小船相对于岸的速度大小为
【答案】C
【详解】B．由于船头方向与河岸垂直，可知此时小船的渡河时间最短，故B错误；
ACD．小船相对于岸的速度大小为设合速度与河岸的夹角为，则有
解得可知小船的实际运动轨迹与岸不垂直，故C正确，AD错误。故选C。
【针对训练2】如图所示，河水流速以及渡船在静水中的划行速度大小均恒定，渡船从平直河岸边的A处开始渡河，当船头方向垂直河岸时，渡船到达正对岸岸边B处下游的C处，A、C连线与水流方向的夹角为60°。若要使渡船从A处开始渡河，能够沿直线到达B处，则船头方向与水流反方向的夹角θ的正切值应为（ ）
A．B．C．D．
【答案】A
【详解】设船在静水中的速度为v1，水速为v2，则当船垂直渡河时得
故选A。
三、关联速度问题
■方法归纳
绳、杆关联问题是指物拉绳(杆)或绳(杆)拉物问题．高中阶段研究的绳都是不可伸长的，杆都是不可伸长和不可压缩的，即绳或杆的长度不会改变，所以解题的原则是：把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相等求解．常见的模型如图所示．

【例3】如题图所示，汽车通过绳子绕过定滑轮连接重物M一起运动，不计滑轮摩擦和绳子质量，已知重物M以v匀速向上运动，连接汽车的轻绳与水平方向夹角为θ，汽车的速度用v汽表示。则（ ）
A．B．
C．汽车做匀速运动D．汽车做匀加速运动
【答案】B
【详解】AB．将汽车速度沿绳与垂直于绳分解，沿绳的分速度与重物速度相等，则解得
A错误，B正确；
CD．根据上述，重物M以v匀速向上运动，当汽车向左运动时，减小，可知汽车速度减小，即汽车 减速运动，CD错误。故选B。
【针对训练3】A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体B以的速度向左匀速运动，如图所示，当绳被拉成与水平面夹角分别是、时。物体A的运动速度为（绳始终有拉力）（ ）
A．B．C．D．
【答案】B
【详解】将A物体的速度沿着绳子方向与垂直绳子方向进行分解，则有沿着绳子方向的速度大小为；将B物体的速度沿着绳子方向与垂直绳子方向进行分解，则有沿着绳子方向的速度大小为。由于沿着绳子方向速度大小相等，故有所以物体A的运动速度为故选B。
【巩固提升】
1．质量为2kg的质点在xOy平面上做曲线运动，在x方向的速度图像和y方向的位移图像如图所示，下列说法中正确的是（ ）
A．质点的初速度大小为3m/s
B．质点所受的合外力为3N，做匀变速曲线运动
C．2s内质点的位移大小约为17m
D．2s末质点速度大小为6m/s
【答案】B
【详解】A．由x方向的速度图像可知，初速度为3m/s，由y方向的位移图像可知在y方向做匀速直线运动，速度为vy=4 m/s，由平行四边形定则可知，质点的初速度为故A错误；
B．由x方向的速度图像可知，在x方向的加速度为1.5 m/s2，受力Fx=3 N，由y方向的位移图像可知在y方向做匀速直线运动，受力Fy=0，所以质点的合力为3N，由于质点的初速度方向与合外力方向不在一条直线上，所以质点做匀加速曲运动，故B正确；
C．2s内x轴方向的位移为，y轴方向的位移为所以质点在2s末内的位移为故C错误；
D．2s末x轴方向的速度为，，y轴方向的速度为：，所以质点在2s末的速度为
故D错误。故选B。
2．在我校某周年校庆活动上，一小型无人机在空中航拍，将其运动沿水平方向和竖直方向分解，水平位移x随时间t变化的图像如图甲所示，竖直方向的速度随时间变化的图像如图乙所示。关于无人机的运动，下列说法正确的是（ ）
A．内做匀加速曲线运动B．时速度大小为
C．内加速度大小为D．内位移大小为
【答案】A
【详解】A．由图可知，在水平方向一直做匀速直线运动，在竖直方向上，在内，做匀加速直线运动，因此在内，物体的合运动为匀加速曲线运动，故A正确；
B．时，由图可知，水平速度，竖直速度，故故B错误；
C．s内，水平加速度为零，竖直加速度也为零，故加速度为零，故C错误；
D．s内，水平位移为4m，竖直位移为合位移为
故D错误。故选A。
3．物体在直角坐标系xOy所在的平面内由O点开始运动，x轴方向的加速度随时间变化图像如图a所示，y轴方向速度随时间变化的图像如图b所示，物体的初速度为2m/s，则对该物体运动过程的描述正确的是（ ）
A．物体在0～2s做直线运动，在2s～3s做曲线运动
B．物体在0～2s的加速度大小为，2s～3s的加速度大小为
C．物体在0～2s和2s～3s内位移之比为
D．物体2s末速度最大，最大值为
【答案】D
【详解】A．物体在0～2s内，x方向做ax1=1m/s2的匀加速运动，y方向做匀速运动，可知合运动是曲线运动；
在2s～3s内，y方向的加速度为，x方向做初速度vx=2m/s，加速度为ax=2m/s2的匀减速运动；y方向做初速度vy=2m/s，加速度为ay2=2m/s2的匀减速运动，则合加速度方向与合初速度方向共线，可知物体做直线运动。
选项A错误；
B．物体在0～2s的加速度大小为a=ax1=1m/s2；2s～3s内ax2=1m/s2；则2s～3s的加速度大小为
选项B错误；
C．物体在0～2s内位移x1=；合位移
2s～3s内位移的位移；合位
则之比为选项C错误；
D．因2s末在x方向和y方向都要做匀减速运动，可知物体2s末速度最大，最大值为
选项D正确。故选D。
4．民族运动会上有一直线侧向骑射项目如图所示，运动员骑在沿直线奔跑的马上，弯弓放箭射击跑道外侧的固定目标，假设运动员骑马奔驰的速度为v1，运动员静止时射出的弓箭速度为v2，跑道距离固定目标的最近距离为d，要想命中目标且射出的箭在空中飞行时间最短（不考虑空气阻力的影响），则（ ）
A．运动员放箭处离目标的距离为
B．运动员放箭处离目标的距离为
C．箭射到固定目标的最短时间为
D．箭射到固定目标的最短时间为
【答案】B
【详解】要想在最短的时间内射中目标，箭应该垂直于马的运动方向射出，如图所示
箭在空中的运动时间为其合运动速度为则放箭处离目标的距离为
故ACD错误，B正确。故选B。
5．唐僧、悟空、沙僧和八戒师徒四人想划船渡过一条宽150m的河，他们在静水中划船的速度大小为3m/s，河水的流速为5m/s，对于这次划船过河，他们有各自的看法，其中正确的是（ ）
A．唐僧说：我们要想到达正对岸就得朝着正对岸划船，最短时间需要50s
B．悟空说：我们要想节省时间就得朝着正对岸划船，最短时间需要30s
C．沙僧说：我们要想少走点路就得朝着正对岸划船。最短路程需要150m
D．八戒说：今天这种情况我们是不可能到达正对岸的，渡河最短路程需要250m
【答案】D
【详解】AB．因在静水中划船的速度大小为3m/s，河水的流速为5m/s，大于船在静水的速度，时间最短时需要朝着正对岸划船，最短时间但此时船要到达正对岸的下游，不可能到达正对岸，故AB错误；
C．因船速小于河水流速，则合速度方向不可能垂直正对岸，即船不可能到达正对岸，最小位移不可能是150m，选项C错误；
D．当合速度与船速度垂直时，渡河的位移最小，此时船头偏向上游，但渡河位移要偏向下游，最短路程
因此D正确。故选D。
6．如图，阿玮要渡过湍急的河水游到河对岸去，已知水流的速度是2m/s，阿玮游泳的速度是1m/s，岸宽30m，阿玮想尽量不被水冲得太远，则到达对岸时，偏离正对岸的最小距离为（ ）
A．30mB．C．D．60m
【答案】C
【详解】如图
阿玮到达对岸时，要偏离正对岸的距离最小，则需要游泳的方向与阿玮的合速度方向垂直，所以
则由可得阿玮到达对岸时，偏离正对岸的最小距离
故选C。
7．一条船要在最短时间内渡过宽为100m的河，已知河水的流速与船离河岸的距离变化的关系如图甲所示，船在静水中的速度与时间的关系如图乙所示，则以下判断中正确的是（ ）
A．船渡河的最短时间25s
B．船运动的轨迹可能是直线
C．船在河水中航行的平均加速度大小为
D．船在河水中的最大速度是
【答案】D
【详解】A．当船头垂直河岸时渡河时间最短，则有，A错误；
B．船在垂直河岸方向上做匀速运动，在沿河岸方向上做变速运动，因此轨迹一定是曲线，B错误；
C．船在河水中航行过程，船的速度先增大后减小，但在河岸两边的速度相同，故整个航行过程的速度变化量为，则船在河水中航行的平均加速度大小为，C错误；
D．船在河水中的最大速度为，D正确；
故选D。
8．如图所示，水平固定的光滑细长杆上套有一物块Q，跨过悬挂于O点的轻小光滑圆环的细线一端连接Q，另一端悬挂一物块P。设细线的左边部分与水平方向的夹角为，初始时很小，现将P、Q由静止同时释放，关于P、Q以后的运动，下列说法正确的是（ ）
A．在向90°增大的过程中，P一直处于超重状态
B．当时，P的速度最大
C．当时，Q的速度最大
D．当时，P、Q的速度大小之比是
【答案】C
【详解】A．P从开始运动到到达最低点的过程中，先向下做加速运动，加速度向下，处于失重状态，然后又减速向下运动，加速度向上，处于超重状态，故D错误
BC．当θ=90º时，P的速度为0，位置最低，即为Q到达O点正下方时，此时Q的速度最大，即当θ=90°时，Q的速度最大，P的速度最小，为零；故B错误，C正确；
D．由题可知，P、Q用同一根绳连接，则Q沿绳子方向的速度与P的速度相等，则当时，
解得：故D错误。故选C。
9．如图所示，某救援队利用如下装置转运救灾物资，物资穿在竖直固定光滑杆上，若汽车速度为，物资运动速度为，定滑轮左右两侧轻绳与竖直方向夹角分别为、。不计滑轮质量以及绳与滑轮间的摩擦，下列关系正确的是（ ）
A．B．
C．D．
【答案】D
【详解】如图
汽车的速度等于沿绳子方向和垂直于绳子方向速度的合速度，根据平行四边形定则，有物资的速度等于沿绳子方向和垂直于绳子方向速度的合速度。则有解得故D正确。
故选D。
10．一个半径为R的半圆柱体沿水平方向向右以速度v0匀速运动，在半圆柱体上搁置一根竖直杆，此杆只能沿竖直方向运动，如图所示．当杆与半圆柱体接触点与柱心的连线与竖直方向的夹角为θ，则竖直杆运动的速度为：（ ）
A．v0sinθB．v0tanθC．v0csθD．
【答案】B
【详解】杆子的实际速度是接触点沿切线方向的速度与半圆柱速度的合速度，如图，
根据速度的合成，运用平行四边形定则，得v1=v0tanθ．故B正确，ACD错误．故选B．独立性
一个物体同时参与两个运动，其中的任一个分运动并不会因为有另外的分运动的存在而有所改变。即各分运动是互相独立的、互不影响的
等时性
各个分运动与合运动总是同时开始，同时结束，经历的时间相等。不是同时发生的运动不能进行运动的合成
等效性
各分运动合成起来和合运动效果相同，即分运动与合运动可以“等效替代”
同体性
合运动和它的分运动必须对应同一个物体的运动，一个物体的合运动不能分解为另一个物体的分运动