数学拓展模块一 上册3.2.2 双曲线的几何性质教案设计

这是一份数学拓展模块一 上册3.2.2 双曲线的几何性质教案设计，共7页。教案主要包含了做题方法总结等内容，欢迎下载使用。
授课
题目
3.2 双曲线
选用教材
高等教育出版社《数学》
（拓展模块一上册）
授课
时长
2课时
授课类型
复习课
教学
目标
能区分不同焦点坐标对应的不同方程；
会根据双曲线的方程说出双曲线的几何性质；
能根据条件求出双曲线的标准方程；
逐步提升直观想象、数学运算和数学建模等核心素养。
教学
重点
根据条件求双曲线的标准方程， 根据标准方程分析双曲线的几何性质。
教学
难点
双曲线性质和标准方程。
教学
环节
教学内容
教师 活动
学生 活动
设计 意图
复习
导入
哪位同学和大家分享自己对双曲线的认识，你还记得双曲线哪些知识？
特问，板书展示
提出 问题
引发 思考
思考
分析
回答
帮助 学生 形成 双曲 线知识的整体感知
系统
复习
一、以表格的形式呈现双曲线标准方程以及相关几何性质的知识点：
1.焦点符号表示： 。
2.焦距： 。
3.实轴： 。
4.虚轴： 。
5.数学定义式：||MF1|-|MF2||=2a(a>0)。
6.顶点： 。
7.a、b、c之间的关系：。
8.离心率： 。
讲解
说明
展示 图像 引发 思考
理解
思考
结合
图像
思考
问题
通过 表格填空的形式，逐一对双曲线部分考察内容进行特问、泛问复习
系统
复习
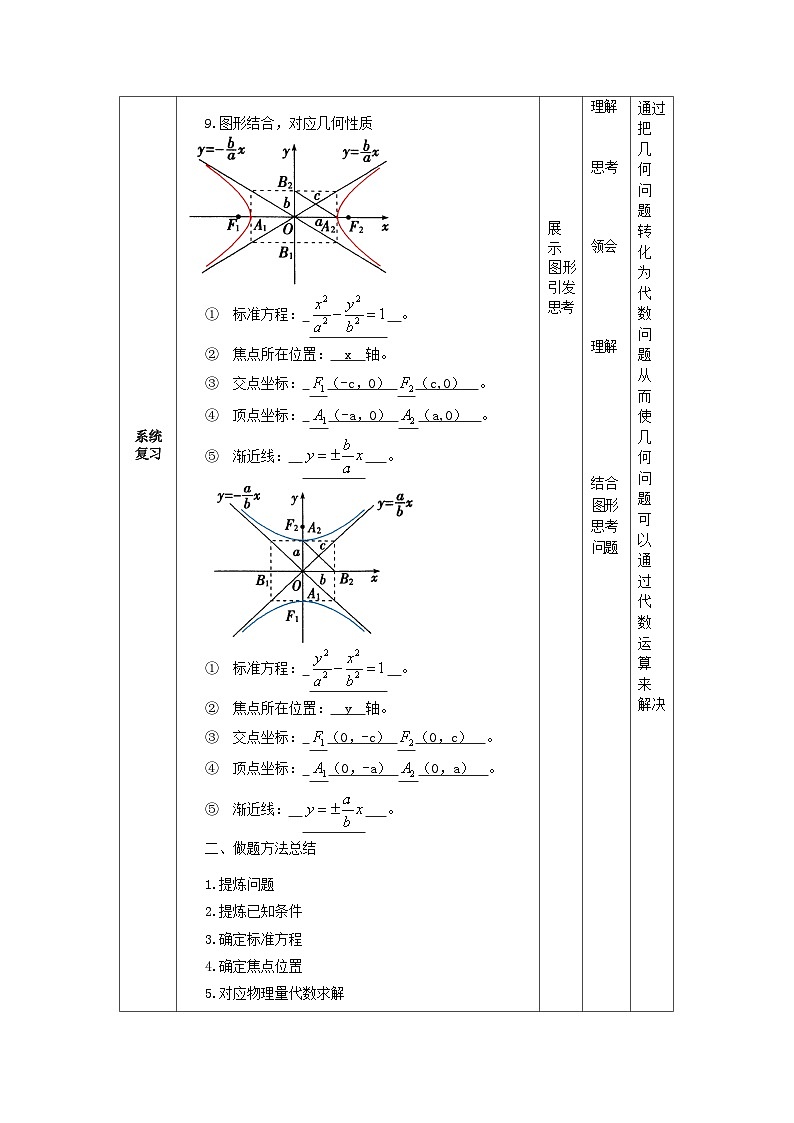
9.图形结合，对应几何性质
标准方程： 。
焦点所在位置： x 轴。
交点坐标： （-c，0） （c,0） 。
顶点坐标： （-a，0） （a,0） 。
渐近线： 。
① 标准方程： 。
② 焦点所在位置： y 轴。
③ 交点坐标： （0，-c） （0，c） 。
④ 顶点坐标： （0，-a） （0，a） 。
⑤ 渐近线： 。
二、做题方法总结
1.提炼问题
2.提炼已知条件
3.确定标准方程
4.确定焦点位置
5.对应物理量代数求解
展示 图形 引发 思考
理解
思考
领会
理解
结合
图形
思考
问题
通过 把几 何问 题转 化为 代数 问题 从而 使几 何问 题可 以通 过代 数运 算来 解决
典型
例题
例 1 已知双曲线C：的左右焦点为， ，点P在双曲线C的右支上，则 。
解：1.提炼问题：
求解的值
2.提炼已知条件：
，
3.确定标准方程：

4.确定焦点位置：
焦点在x轴上
5.对应物理量
，

例 2 双曲线 的实轴长为
解：1.提炼问题：
求解实轴的长度
2.提炼已知条件：
双曲线标准方程
3.确定标准方程：

4.确定焦点位置：
焦点在y轴上
5.对应物理量
，
实轴长度
提问 引导
讲解 强调
指导
思考
分析
解决
交流
主动
求解
让学 生理 解求 解实
际问
题时
的步
骤，
并逐
步熟
练应
用

例 3 双曲线 的虚轴长为
解：1.提炼问题：
求解虚轴的长度
2.提炼已知条件：
双曲线方程
3.确定标准方程：

4.确定焦点位置：
焦点在x轴上
5.对应物理量
，
虚轴长度
例 4 双曲线 的焦距是
解：1.提炼问题：
求解焦距的大小
2.提炼已知条件：
双曲线方程
3.确定标准方程：

4.确定焦点位置：
焦点在x轴上
5.对应物理量
，
，
，
引导学生 先将 双曲 线方 程化 为标 准形 式，再根据解题步骤和方法进行求解
巩固
练习
已知双曲线： （，）的实轴长为4,虚轴长为8,则其渐近线方程为 。
已知双曲线的一个焦点为（5,0），一个顶点为（3,0） ，则双曲线方程的标准方程为。
双曲线的离心率为 ，且过（4，） ,则方程为。
提问
巡视
指导
思考
动手
求解
交流
及时 掌握 学生 掌握 情况 查漏 补缺
归纳
总结
一、双曲线主要知识点
二、做题步骤总结
1.提炼问题
2.提炼已知条件
3.确定标准方程
4.确定焦点位置
5.对应物理量代数求解
引导
提问
回忆
反思
培养学生总结学习过程能力
布置
作业
1.完成相应练习题
2.复习抛物线相关知识点
说明
记录
练习
巩固