初中数学苏科版七年级下册第10章 二元一次方程组10.1 二元一次方程当堂检测题

这是一份初中数学苏科版七年级下册第10章 二元一次方程组10.1 二元一次方程当堂检测题，共8页。试卷主要包含了1　二元一次方程，下列等式，方程a+3b=7的正整数解有等内容，欢迎下载使用。

10.1 二元一次方程
基础过关全练
知识点1 二元一次方程
1.(2023江苏盐城月考)下列等式:①2x+y=4;②3xy=7;③x2+2y=0;④1x-2
=y;⑤2x+y+z=1中,二元一次方程的个数是(M7210001)( )
A.1 B.2 C.3 D.4
2.【生命安全与健康】(2023浙江温州中考)一瓶牛奶的营养成分中,碳水化合物含量是蛋白质的1.5倍,碳水化合物、蛋白质与脂肪的含量共30 g.设蛋白质、脂肪的含量分别为x g,y g,可列出方程为(M7210001)
( )
A.52x+y=30 B.x+52y=30 C.32x+y=30 D.x+32y=30
3.【新独家原创】若方程(a+2 024)x+3y|a|-2 023=1是关于x,y的二元一次方程,则a= .(M7210001)
4.若x与y的3倍的和是16,那么可用二元一次方程表示为 .(M7210001)
知识点2 二元一次方程的解
5.【教材变式·P95练一练T1】(2023江苏无锡中考)下列4组数中,不是二元一次方程2x+y=4的解的是( )
A.x=1y=2 B.x=2y=0 C.x=0.5y=3 D.x=−2y=4
6.关于x、y的方程ax-(a-1)y=a+2有一个与a的值无关的解,这个解是 .
7.已知m=2,n=3是关于m,n的二元一次方程3m+an=18的一组解.
(1)求a的值;
(2)请用含有m的代数式表示n.
知识点3 求二元一次方程的部分解
8.方程a+3b=7的正整数解有( )
A.1组 B.2组 C.3组 D.4组
能力提升全练
9.(2023江苏南京高淳期中,4,★☆☆)已知方程xa-1-2y2+b+3=0是关于x、y的二元一次方程,则a+b的值为(M7210001)( )
A.1 B.-1
C.3 D.-3
10.(2023江苏盐城月考,6,★★☆)已知二元一次方程x+y=1,下列说法正确的是( )
A.它有一组正整数解
B.它只有有限组解
C.它只有一组非负整数解
D.它的整数解有无数组
11.(2023黑龙江齐齐哈尔中考,9,★★☆)为提高学生学习兴趣,增强动手实践能力,某校为物理兴趣小组的同学购买了一根长度为150 cm的导线,将其全部截成10 cm和20 cm两种长度的导线用于实验操作(每种长度的导线至少有一根),则截取方案共有(M7210001)( )
A.5种 B.6种
C.7种 D.8种
12.(2022四川雅安中考,16,★★☆)已知x=1,y=2是方程ax+by=3的解,则代数式2a+4b-5的值为 .
13.(2023江苏苏州太仓期中,21,★★☆)某手机店计划用6万元从厂家购进若干部新型手机,以满足市场需求.已知该厂家生产三种不同型号的手机,出厂价分别为甲型号手机1 800元/部,乙型号手机600元/部,丙型号手机1 200元/部,若手机店同时购进三种不同型号的手机共40部,并将6万元恰好用完,且要求乙型号手机的购买数量不少于6部且不多于8部,试求手机店每种型号手机的购买数量.(M7210001)
素养探究全练
14.【新考向·新定义试题】【运算能力】把y=ax+b(其中a,b是常数,x,y是未知数)这样的方程称为“雅系二元一次方程”.当y=x时,“雅系二元一次方程”y=ax+b中x的值称为“雅系二元一次方程”的“完美值”.例如:当y=x时,“雅系二元一次方程”y=3x-4化为x=3x-4,其“完美值”为x=2.
(1)求“雅系二元一次方程”y=5x-6的“完美值”;
(2)若x=-3是“雅系二元一次方程”y=13x+m的“完美值”,求m的值;
(3)是否存在n,使得“雅系二元一次方程”y=-32x+n与y=3x-n+1(n是常数)的“完美值”相同?若存在,请求出n的值及此时的“完美值”;若不存在,请说明理由.
答案全解全析
基础过关全练
1.A ①2x+y=4是二元一次方程;②3xy=7是二元二次方程;③x2+2y=0是二元二次方程;④1x-2=y不是整式方程,故不是二元一次方程;⑤2x+y+z=1是三元一次方程.故选A.
2.A ∵碳水化合物含量是蛋白质的1.5倍,且蛋白质的含量为x g,
∴碳水化合物的含量是1.5x g.
根据题意,得1.5x+x+y=30.∴52x+y=30.故选A.
3.答案 2 024
解析 因为方程(a+2 024)x+3y|a|-2 023=1是关于x,y的二元一次方程,所以a+2 024≠0,|a|-2 023=1.解得a=2 024.
4.答案 x+3y=16
解析 y的3倍是3y.根据题意,得x+3y=16.
5.D A.把x=1,y=2代入方程,左边=4=右边,所以是方程的解;
B.把x=2,y=0代入方程,左边=4=右边,所以是方程的解;
C.把x=0.5,y=3代入方程,左边=4=右边,所以是方程的解;
D.把x=-2,y=4代入方程,左边=0≠右边,所以不是方程的解.
故选D.
6.答案 x=3y=2
解析 ∵ax-(a-1)y=a+2,
∴a(x-y-1)=2-y,
∵方程有一个与a的值无关的解,
∴x-y-1=0,2-y=0,∴y=2,
将y=2代入x-y-1=0,可得x=3,
∴这个解为x=3,y=2.
7.解析 (1)将m=2,n=3代入3m+an=18,得
3×2+3a=18,解得a=4.
(2)∵a=4,
∴原方程为3m+4n=18,
∴4n=18-3m,
∴n=18−3m4.
8.B 因为a+3b=7,所以a=7-3b.
又因为a,b均为正整数,
所以a=4,b=1或a=1,b=2,
所以方程a+3b=7的正整数解有2组.故选B.
能力提升全练
9.A 根据题意,得a-1=1,2+b=1.
解得a=2,b=-1.所以a+b=2-1=1.故选A.
10.D 方程x+y=1没有正整数解,故A选项错误.方程x+y=1的解有无数组,故B选项错误.方程x+y=1的非负整数解为x=1,y=0和x=0,y=1,共两组,故C选项错误.方程x+y=1的整数解有无数组,故D选项正确.
故选D.
11.C 设截成10 cm的导线有x根,截成20 cm的导线有y根.
根据题意,得10x+20y=150,∴x=15-2y,
∴方程的正整数解为
x=13,y=1;x=11,y=2;x=9,y=3;x=7,y=4;x=5,y=5;x=3,y=6;x=1,y=7.
故截取方案共有7种.故选C.
12.答案 1
解析 把x=1,y=2代入ax+by=3,得a+2b=3,
则2a+4b-5=2(a+2b)-5=2×3-5=6-5=1.
13.解析 设手机店购进x部甲型号手机,y部乙型号手机,则购进(40-x-y)部丙型号手机.
根据题意,得1 800x+600y+1 200(40-x-y)=60 000,
∴x=y+20.
又∵x,y,40-x-y均为正整数,且6≤y≤8,
∴x=26,y=6或x=27,y=7或x=28,y=8,
∴该手机店共有3种进货方案.
方案一:购进26部甲型号手机,6部乙型号手机,8部丙型号手机;
方案二:购进27部甲型号手机,7部乙型号手机,6部丙型号手机;
方案三:购进28部甲型号手机,8部乙型号手机,4部丙型号手机.
素养探究全练
14.解析 (1)当y=x时,“雅系二元一次方程”y=5x-6化为x=5x-6,解得x=32,所以“雅系二元一次方程”y=5x-6的“完美值”为x=32.
(2)因为x=-3是“雅系二元一次方程”y=13x+m的“完美值”,所以-3=13×(-3)+m,解得m=-2.
(3)存在n,使得“雅系二元一次方程”y=-32x+n与y=3x-n+1(n是常数)的“完美值”相同,理由如下:
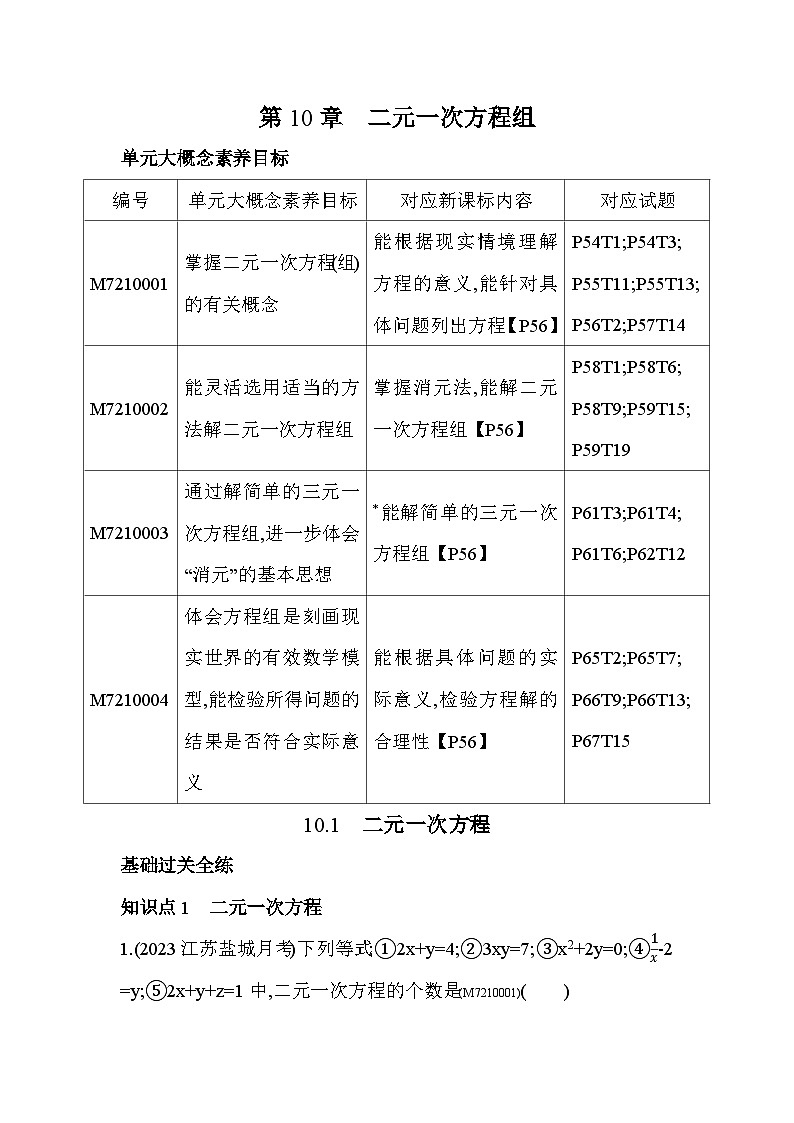
由x=-32x+n,得x=25n.由x=3x-n+1,得x=n-12,所以25n=n-12,解得n=5,所以x=2,所以当n=5时,“雅系二元一次方程”y=-32x+n与y=3x-n+1的“完美值”相同,“完美值”为x=2.编号
单元大概念素养目标
对应新课标内容
对应试题
M7210001
掌握二元一次方程(组)的有关概念
能根据现实情境理解方程的意义,能针对具体问题列出方程【P56】
P54T1;P54T3;
P55T11;P55T13;P56T2;P57T14
M7210002
能灵活选用适当的方法解二元一次方程组
掌握消元法,能解二元一次方程组【P56】
P58T1;P58T6;
P58T9;P59T15;
P59T19
M7210003
通过解简单的三元一次方程组,进一步体会“消元”的基本思想
*能解简单的三元一次方程组【P56】
P61T3;P61T4;
P61T6;P62T12
M7210004
体会方程组是刻画现实世界的有效数学模型,能检验所得问题的结果是否符合实际意义
能根据具体问题的实际意义,检验方程解的合理性【P56】
P65T2;P65T7;
P66T9;P66T13;
P67T15