

2023-2024学年浙江省宁波市镇海区蛟川书院九年级(下)开学数学试卷-普通用卷
展开1.若2x=5y,则xy的值是( )
A. 25B. 52C. 45D. 54
2.如图,一块矩形ABCD绸布的长AB=a,宽AD=1,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
A. 2B. 3C. 2D. 5
3.如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )
A. π6B. π4C. π3D. π2
4.为测量操场上篮筐的高AB,小明站在点Q处的眼睛P与地面的距离PQ为1.7米,与AB的距离PC为2.5米,若仰角∠APC为θ,则篮筐的高AB可表示为( )
A. (1.7+2.5tanθ)米
B. (1.7+2.5tanθ)米
C. (1.7+2.5sinθ)米
D. (1.7+2.5sinα)米
5.如图,在⊙O中,AB是弦,C是弧AB上一点.若∠OAB=25°,∠OCA=40°,则∠BOC的度数为( )
A. 30°
B. 40°
C. 50°
D. 60°
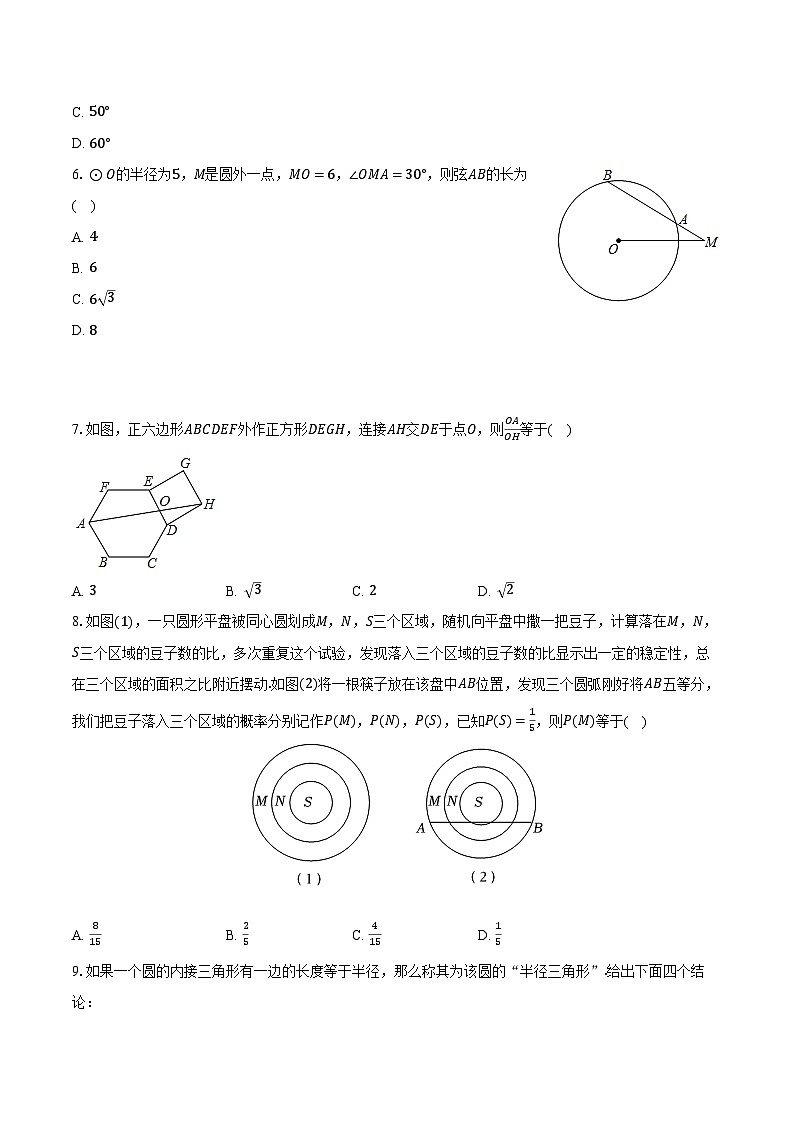
6.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A. 4
B. 6
C. 6 3
D. 8
7.如图,正六边形ABCDEF外作正方形DEGH,连接AH交DE于点O,则OAOH等于( )
A. 3B. 3C. 2D. 2
8.如图(1),一只圆形平盘被同心圆划成M,N,S三个区域,随机向平盘中撒一把豆子,计算落在M,N,S三个区域的豆子数的比,多次重复这个试验,发现落入三个区域的豆子数的比显示出一定的稳定性,总在三个区域的面积之比附近摆动.如图(2)将一根筷子放在该盘中AB位置,发现三个圆弧刚好将AB五等分,我们把豆子落入三个区域的概率分别记作P(M),P(N),P(S),已知P(S)=15,则P(M)等于( )
A. 815B. 25C. 415D. 15
9.如果一个圆的内接三角形有一边的长度等于半径,那么称其为该圆的“半径三角形”.给出下面四个结论:
①一个圆的“半径三角形”有无数个;
②一个圆的“半径三角形”可能是锐角三角形、直角三角形或钝角三角形;
③当一个圆的“半径三角形”为等腰三角形时,它的顶角可能是30°,120°或150°;
④若一个圆的半径为2,则它的“半径三角形”面积最大值为2 3.
上述结论中,所有正确结论的序号是( )
A. ①②B. ②③C. ①②③D. ①②④
10.当a≠b时,将(a,b),(b,a)两个点称为一对“关联的对称点”.若抛物线y=−x2+x+c(c是常数)总存在一对“关联的对称点”,则c的取值范围是( )
A. c<2B. c<1C. c>2D. c>1
二、填空题:本题共6小题,每小题5分,共30分。
11.二次函数y=2x2+4x+5的顶点坐标为______.
12.如图,AB、CD为⊙O的两条弦,若∠B+∠C=90°,AB2+CD2=100,则⊙O的半径为______.
13.如图,D、E分别是△ABC的边AB、BC上的点,DE//AC,若S△DOE:S△COA=1:25,则S△BDE:S△CDE= ______.
14.如图,四边形ABCD内接于半径为2 3的圆,∠A=120°,∠B=45°,AB=AD,则四边形ABCD的周长为______.
15.贴春联是中国传统习俗,晓红老家有个圆形拱门,每年都会贴上长长的春联,看上去非常喜庆.晓红用圆弧近似模拟拱门,经测量发现,ADB的拱高CD和其所对的弦AB都是2m,EB所对的圆心角是150°,弦AB与春联的底端平齐,E点正好是春联外侧最高点,则春联的外侧长度大约是______m.(参考数据 3=1.732,结果按四舍五入法精确到0.1)
16.已知抛物线y=x2−3mx+2m2−1(m>0)与直线y=−1相交于点A,B(点B在点A右侧),且AB=2.
(1)m的值是______.
(2)直线x=n(2≤n≤4)与抛物线y=x2−3mx+2m2−1相交于点P,与直线y=kx−2(k>0)相交于点Q,l=PQ.若l随n的增大而增大,则k的取值范围是______.
三、解答题:本题共3小题,共24分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
求下列各式的值:
(1)sin45°cs45°+4tan30°sin60°;
(2)cs60°−2sin245°+23tan260°−sin30°.
18.(本小题8分)
如图,已知二次函数图象与y轴交点为C(0,3),其顶点为D(1,2).
(1)求二次函数的表达式;
(2)将二次函数图象平移,使其顶点与原点重合,然后将其图象绕O点顺时针旋转90°得到抛物线G,如图,直线y=−x+2与G交于A,B两点,P为G上位于直线AB左侧一点,求△ABP面积最大值,及此时点P的坐标.
19.(本小题8分)
已知锐角△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,交AD于点G,交⊙O于点F,连结AF.连结CF,AD=BD.
(1)直接写出CF与GD的数量关系;
(2)如图,连结OD,OG,在BG上取点M,使得∠BDM=∠ACF,DM=2 2,BG=5,求△ODG的面积.
答案和解析
1.【答案】B
【解析】解:∵2x=5y,
∴xy=52.
故选:B.
利用内项之积等于外项之积进行判断.
本题考查了比例的性质:熟练掌握比例的性质(内项之积等于外项之积,合比性质,分比性质,合分比性质,等比性质).
2.【答案】B
【解析】【分析】
此题考查了相似多边形的性质.注意相似多边形的对应边成比例.由裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,构建方程求解即可.
【解答】
解:∵使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,
∴1a=13a1,
解得a= 3或− 3(舍弃),
∴a= 3,
故选B.
3.【答案】C
【解析】【分析】
此题主要考查菱形、等边三角形的性质以及弧长公式的理解及运用.
连接AC,根据题意可得△ABC为等边三角形,从而可得到∠BAC的度数,再根据弧长公式求得弧BC的长度.
【解答】
解:连接AC,可得AB=BC=AC=1,则∠BAC=60°,根据弧长公式,可得
弧BC的长度等于60π×1180 =π3
故选C.
4.【答案】A
【解析】解:由题意得,PQ=BC=1.7米,PC=2.5米,
在Rt△APC中,∵∠APC=θ,
∴tan∠APC=tanθ=ACPC=AC2.5,
∴AC=2.5tanθ,
∴AB=AC+BC=(1.7+2.5tanθ)(米),
故选:A.
由题意得到PQ=BC=1.7米,PC=2.5米,解直角三角形即可得到结论.
本题考查了解直角三角形的应用−仰角俯角,利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
5.【答案】A
【解析】解:∵OA=OB,∠OAB=25°,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°−∠OAB−∠OBA=130°,
∵OA=OC,∠OCA=40°,
∴∠OAC=∠OCA=40°,
∴∠AOC=180°−∠OAC−∠OCA=100°,
∴∠BOC=∠AOB−∠AOC=130°−100°=30°,
故选:A.
根据等腰三角形的性质求出∠OBA=∠OAB=25°,∠OAC=∠OCA=40°,再根据三角形内角和定理求出∠AOB和∠AOC,再求出答案即可.
本题考查了圆心角、弧、弦之间的关系,等腰三角形的性质和三角形的内角和定理等知识点,能灵活运用知识点进行推理和计算是解此题的关键.
6.【答案】D
【解析】解:过O作OC⊥AB于C,连接OA,则∠OCA=90°,
∵MO=6,∠OMA=30°,
∴OC=12MO=3,
在Rt△OCA中,由勾股定理得:AC= OA2−OC2= 52−32=4,
∵OC⊥AB,OC过O,
∴BC=AC,
即AB=2AC=2×4=8,
故选:D.
过O作OC⊥AB于C,连接OA,根据含30°角的直角三角形的性质得出OC=12MO=3,根据勾股定理求出AC,再根据垂径定理得出AB=2AC,最后求出答案即可.
本题考查了含30°角的直角三角形的性质,勾股定理,垂径定理等知识点,能熟记垂直于弦的直径平分弦是解此题的关键.
7.【答案】B
【解析】解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD= 3a.
∵OD//AB,
∴OAOH=BDDH= 3aa= 3,
故选:B.
连接BD,如图所示:由正六边形和正方形的性质得:B、D、H三点共线,设正六边形的边长为a,则AB=BC=CD=DE=a,解直角三角形求出BD,再利用平行线分线段成比例定理解决问题即可.
本题考查正多边形与圆,正方形的性质,解直角三角形等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
8.【答案】A
【解析】解:如图2,设AE=EC=CD=DF=BF=2x,
过O点作OH⊥CD于H,连接OC、OE、OA,则CH=DH=x,
∵P(S)=15,
∴π⋅OC2π⋅OA2=15,
解得OA= 5OC,
在Rt△OAH中,OH2=OA2−AH2=( 5OC)2−(5x)2=5OC2−25x2,
在Rt△OCH中,OH2=OC2−CH2=OC2−x2,
∴5OC2−25x2=OC2−x2,
解得OC= 6x,
∴OH2=5x2,OA= 30x,
在Rt△OEH中,OE2=OH2+EH2=5x2+9x2=14x2,
∴P(M)=π⋅OA2−π⋅OE2π⋅OA2=π⋅30x2−π⋅14x2π⋅30x2=815.
故选:A.
如图2,设AE=EC=CD=DF=BF=2x,过O点作OH⊥CD于H,连接OC、OE、OA,根据垂径定理得到CH=DH=x,再利用几何概率的求法得到π⋅OC2π⋅OA2=15,则OA= 5OC,接着利用勾股定理,在Rt△OAH中有OH2=5OC2−25x2,在Rt△OCH中有OH2=OC2−x2,所以5OC2−25x2=OC2−x2,则OC= 6x,于是可表示出OH2=5x2,OA= 30x,OE2=14x2,然后根据几何概率的求法计算M区域的面积与整个面积的比即可.
本题考查了几何概率问题,某事件的概率=这个事件所占的面积与总面积之比.利用运用垂径定理和勾股定理表示出各圆的半径是解决问题的关键.
9.【答案】C
【解析】解:如图,AB=OA,即AB的长度等于半径,
以AB为边的圆的内接三角形有无数个,
∴一个圆的“半径三角形”有无数个,故①结论正确;
∵OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
当点C在优弧AB上时,∠C=30°,
当点C在劣弧AB上时,∠C=150°,
当点C在圆上移动时,∠CAB可能是90°,
∴一个圆的“半径三角形”可能是锐角三角形、直角三角形或钝角三角形,故②结论正确;
由以上可知,∠C可以是30°或150°,
当AC=AB,∠C=30°时,∠CAB=180°−30°3−30°=120°,
∴当一个圆的“半径三角形”为等腰三角形时,它的顶角可能是30°,120°或150°,故③结论正确;
过点O作OH⊥AB于H,
则AH=HB=12AB=1,
∴OH= OA2−AH2= 3,
当点C为优弧AB的中点时,△ABC的面积最大,最大面积为:12×2×(2+ 3)=2+ 3,故④结论错误;
故选:C.
根据圆的“半径三角形”的概念判断①②;根据圆周角定理、等腰三角形的概念判断③;根据垂径定理求出AH,根据勾股定理求出OH,求出△ABC的最大面积,判断④.
本题考查的是三角形的外接圆与外心,掌握圆周角定理、等腰三角形的性质、灵活运用分情况讨论思想是解题的关键.
10.【答案】D
【解析】解:由题知,
将(a,b)和(b,a)代入函数解析式得,
−a2+a+c=b−b2+b+c=a,
两式相减得,
(a+b)(a−b)=2(a−b),
又因为a≠b,
所以a+b=2,
则b=2−a,
所以−a2+a+c=2−a,
所以c=a2−2a+2=(a−1)2+1,
又因为a=1时,b=1,与条件矛盾,
所以a≠1,
所以c>1.
故选:D.
将(a,b)和(b,a)代入函数解析式,发现a,b之间的关系,再表示出c即可解决问题.
本题考查二次函数图象与系数的关系,熟知二次函数的图象和性质是解题的关键.
11.【答案】(−1,3)
【解析】解:y=2x2+4x+5=2(x+1)2+3,
∴顶点坐标为:(−1,3),
故答案为:(−1,3).
将二次函数转化为顶点式,直接写出顶点坐标即可.
本题考查二次函数的性质,熟练掌握二次函数的性质是解题的关键.
12.【答案】5
【解析】解:如图,连接DO并延长交⊙O于点E,连接CE,
∵DE是⊙O的直径,
∴∠DCE=90°,
∴∠BCD+∠BCE=90°,CE2+CD2=DE2,
∵∠B+∠BCD=90°,
∴∠BCE=∠ABC,
∴BE=AC,
∴CE=AB,
∴CE=AB,
∵AB2+CD2=100,
∴CE2+CD2=100,
即DE2=100,
∴DE=10,
∴OD=5,
即⊙O的半径为5.
故答案为:5.
构造直径DE,由∠BCD+∠BCE=90°和∠ABC+∠BCD=90°证明∠BCE=∠ABC,得到CE=AB,根据勾股定理求出直径DE即可得到答案.
本题考查了圆周角和勾股定理等有关知识,解题的关键是“根据直径所对的圆周角是直角”构造直角三角形.
13.【答案】14
【解析】解:∵DE//AC,
∴△DOE∽△COA,
∴S△DOES△COA=(DECA)2=125,
∴DECA=15,
∵DE//AC,
∴△BDE∽△BAC,
∴BDBA=DECA=15,
∴BDDA=14,
∴S△BDES△ADE=BDDA=14,
故答案为14.
由DE//AC,可判定△DOE∽△COA,△BDE∽△BAC,再根据相似三角形的性质及等高三角形的性质求解即可.
本题考查了相似三角形的判定与性质,熟练掌握相似三角形的的面积比等于相似比的平方是解题的关键.
14.【答案】4 3+6 2
【解析】解:连接AC,BD,
由题意得BDsin∠BAD=ACsin∠ABC=4 3,
又∠A=120°,∠B=45°,
∴BD=6,AC=2 6.
在△ABD中,∠BAD=120°,AB=AD,BD=6,
∴AB=AD=2 3.
∵四边形ABCD内接于半径为2 3的圆,它的对角互补,
∴AC⋅BD=AB⋅DC+AD⋅BC.
∴12 6=2 3(BC+CD).
∴BC+CD=6 2.
∴四边形ABCD的周长为4 3+6 2.
故答案为:4 3+6 2.
连接AC,BD.利用正弦定理求出BD=6,AC=2 6,AB=AD=2 3,再利用托勒密定理求出BC+CD=6 2,即可得解.
本题主要考查三角形中的几何计算,考查运算求解能力,属于中档题.
15.【答案】1.9
【解析】解:过点E作EG⊥AB,延长EO交AB于点F,过点F作FH⊥OB,如图:
由垂径定理可得AC=BC=1,
在Rt△BOC中,OB2=OC2+BC2,即OB2=(2−OB)2+1,
解得OB=54,
∴OC=34,
∵∠EOB=150°,
∴∠FOH=30°,
设FH=a,则OF=2a,OH= 3a,BH=54− 3a,
∴tan∠OBC=OCBC=FHBH,即341=a54− 3a,
解得a=45 3−6044,
∴OF=45 3−6022,
∴EF=54+45 3−6022=90 3−6544,
∴sin∠EFG=EGEF=OCOF,
∴EG90 3−6544=3445 3−6022,
解得EG=90 3−65120 3−160≈1.9cm.
过点E作EG⊥AB,延长EO交AB于点F,过点F作FH⊥OB,由题意可求出OC=34,OB=54,由∠EOB=150°得出∠FOH=30°,设FH=a,则OF=2a,OH= 3a,BH=54− 3a,易得△BHF∽△BCO,利用相似比即可求出a,进而求出OF,EF,再应用锐角三角函数即可求出EG.
本题考查解直角三角形的应用,垂径定理,正确作出辅助线是解题关键.
16.【答案】2 k≤−2
【解析】解:(1)设抛物线y=x2−3mx+2m2−1(m>0)与直线y=−1相交于点A(x1,0),B(x2,0),则x1,x2是方程x2−3mx+2m2−1=−1的两个实数根,
∴x1+x2=3m,x1⋅x2=2m2,
∵AB=2,
∴|x2−x1|=2,
∴(x1+x2)2−4x1x2=4,
即9m2−8m2=4,
解得m=±2,
∵m>0
∴m的值为2;
故答案为:2;
(2)∵m=2,
∴抛物线为y=x2−6x+7,
∵直线x=n(2≤n≤4)与抛物线y=x2−3mx+2m2−1相交于点P,与直线y=kx−2(k>0)相交于点Q,
∴P(n,n2−6n+7),Q(n,kn−2),
当2≤n≤4时,l随n的增大而增大,
l=PQ=(kn−2)−(n2−6n+7)=−n2+(k+6)n−9=−(n−k+62)2+k2+124,
∵−1<0,
∴当n≤k+62时,l的值随n的增大而增大,
∵2≤n≤4,
∴k+62≥4,
∴k≥2,
故答案为:k≥2.
(1)设抛物线y=x2−3mx+2m2−1(m>0)与直线y=−1相交于点A(x1,0),B(x2,0),则x1,x2是方程x2−3mx+2m2−1=−1的两个实数根,由AB=2,得(x1+x2)2−4x1x2=4,即9m2−8m2=4,可解得m=2;
(2)利用函数的解析式用n表示出点P,Q的坐标,进而求得线段PQ,利用配方法结合函数的图象即可列出关于k的不等式,解不等式则结论可得.
本题主要考查了二次函数图象与系数的关系,一次函数图象与系数的关系,一次函数图象上点的坐标的特征,抛物线上点的坐标的特征,二次函数与方程的关系,熟练掌握二次函数的性质是解题的关键.
17.【答案】解:(1)原式= 22× 22+4× 33× 32
=12+2
=52;
(2)原式=12−2×( 22)2+23×( 3)2−12
=12−2×12+23×3−12
=12−1+2−12
=1.
【解析】(1)直接利用特殊角的三角函数值进而分别代入得出答案;
(2)直接利用特殊角的三角函数值进而分别代入得出答案.
此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
18.【答案】解:(1)∵顶点D(1,2),
设二次函数的解析式为y=a(x−1)2+2,
把(0,3)代入得:3=a+2,
∴a=1,
∴y=(x−1)2+2,
即y=x2−2x+3;
(2)二次函数平移后顶点与原点重合时顶点为(0,0),
则函数的解析式为:y=x2,
设F(m,m2)为y=x2上一点,
F绕O顺时针旋转90°后,对应点为F′,
则△FMO≌△F′M′O,
则FM=F′M=m,FN=OM=OM′=m2,
F′:(m2,−m),
若F在y轴左侧同理可证成立,即满足横坐标为纵坐标的平方,
所以G:x=y2,
把y=−x+2代入x=y2,
∴y2=−y+2,
解得:y1=−2,y2=1;
则A(1,1),B(4,−2),
设:P(m2,m),
过点P作PQ/x轴交AB于点Q,
∵AB:y=−x+2,
∴Q(2−m,m),
∴PQ=2−m−m2,
∴S△ABP=12PQ(yA−yB)
=12(2−m−m2)⋅3
=−32m2−32m+3,
当m=−12时,S△ABP有最大值,Smax=278,
此时P(14,−12).
【解析】(1)由待定系数法即可求解;
(2)由S△ABP=12PQ(yA−yB),即可求解.
本题考查的是二次函数综合运用,涉及到一次函数的基本性质、待定系数法求函数表达式、面积的计算、图象的旋转等,解答本题的关键是熟练掌握二次函数的基本性质.
19.【答案】解:(1)连接CG,
由(1)得∠AGE=∠ACD,
∵∠AGE=∠BGD,
∴∠BGD=∠ACD,
∵BD=AD,∠BDG=∠ADC=90°,
∴△BDG≌△ADC(AAS),
∴DG=DC,
∴△CDG是等腰直角三角形,
∴CG= DG2+DC2= 2DG,
∵GE=FE,CE=CE,∠CEG=∠CEF=90°,
∴△CEG≌△CEF(SAS),
∴CG=CF,
∵CG= 2DG,
∴CF= 2DG;
(2)作OH⊥BC,垂足为点H,
∵OH⊥BC,
∴BH=CH=12BC,
∵CF=CF,
∴∠CBF=∠CAF,
∵∠BDM=∠ACF,
∴△BDM∽△ACF,
∴BDAC=DMCF,
由①得△BDG≌△ADC,CF= 2DG,
∴AC=BG=5,
∵BDAC=DMCF,
∴BD5=2 2 2DG,
∴BD=10DG,
在Rt△BDG中,
∵BD2+DG2=BG2,
∴(10DG)2+DG2=52,
整理得(DG2)2−25DG2+100=0,
解得DG= 5,DG=− 5(不合题意,舍去),DG=2 5,DG=−2 5(不合题意,舍去),
当DG= 5,BD=2 5,
当DG=2 5,BD= 5(不满足BD>DG,舍去),
∴BC=BD+DC=BD+DG=3 5,DH=CH−CD= 52,
∴S△ODG=12DG⋅DH=12× 5× 52=54,
∴△ODG的面积为54.
【解析】(1)CF= 2DG.连接CG,证明△BDG≌△ADC,进而得△CDG是等腰直角三角形,即有CG= 2DG,再证明△CEG≌△CEF,得CG=CF,即可证明结论;
(2)作OH⊥BC,垂足为点H,证明△BDM∽△ACF,得BDAC=DMCF,则有BD=10DG,由BD2+DG2=BG2,解得DG,从而求出BC、DH、DG,即可求出△ODG的面积.
本题考查了同弧所对的圆周角相等,等腰三角形的性质与判定,三线合一,全等三角形的性质与判定,勾股定理,相似三角形的性质与判定,垂径定理,本题的关键是熟练掌握与圆有关的性质,结合相似三角形求出线段的长度从而解决问题.
浙江省宁波市镇海区蛟川书院2023-2024学年九年级下学期开学考试数学试卷: 这是一份浙江省宁波市镇海区蛟川书院2023-2024学年九年级下学期开学考试数学试卷,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年浙江省宁波市镇海区蛟川书院九年级(上)期末数学试卷(含解析): 这是一份2023-2024学年浙江省宁波市镇海区蛟川书院九年级(上)期末数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年浙江省宁波市镇海区蛟川书院七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年浙江省宁波市镇海区蛟川书院七年级(下)期中数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












