资料中包含下列文件,点击文件名可预览资料内容








还剩14页未读,
继续阅读
数学七年级下册第六章 频率初步2 频率的稳定性课堂教学ppt课件
展开
这是一份数学七年级下册第六章 频率初步2 频率的稳定性课堂教学ppt课件,文件包含2023年初中数学北师大版七下课件第六章62频率的稳定性第1课时ppt、2023年初中数学北师大版七下拓展资源第六章62第1课时教学方法引导doc、2023年初中数学北师大版七下拓展资源第六章62第1课时课堂问题处理doc、2023年初中数学北师大版七下拓展资源第六章62第1课时数学史实doc等4份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
抛掷一枚图钉,落地后会 出现两种情况:钉尖朝上 , 钉尖朝下。你认为钉尖朝上和 钉尖朝下的可能性一样 大吗?
小明和小丽在玩抛图钉游戏
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
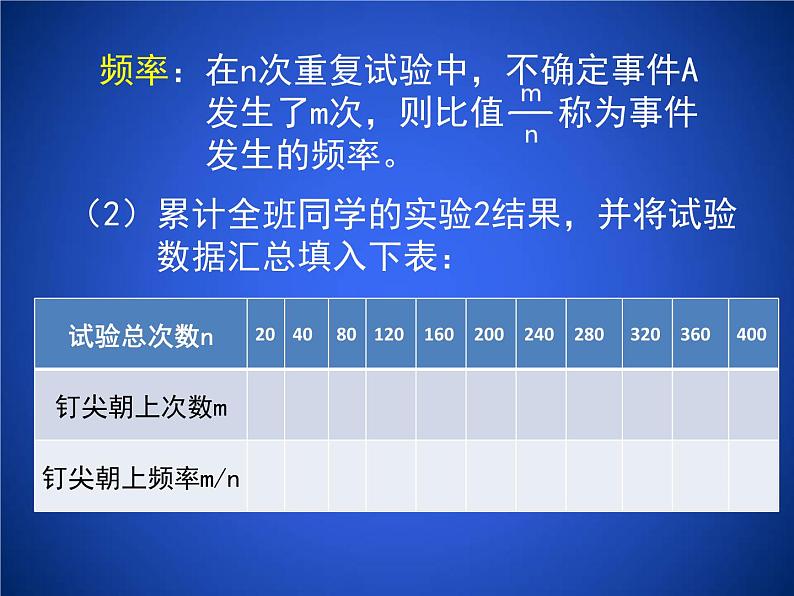
频率:在n次重复试验中,不确定事件A 发生了m次,则比值 称为事件 发生的频率。
(2)累计全班同学的实验2结果,并将试验 数据汇总填入下表:
(3)根据上表完成下面的折线统计图:
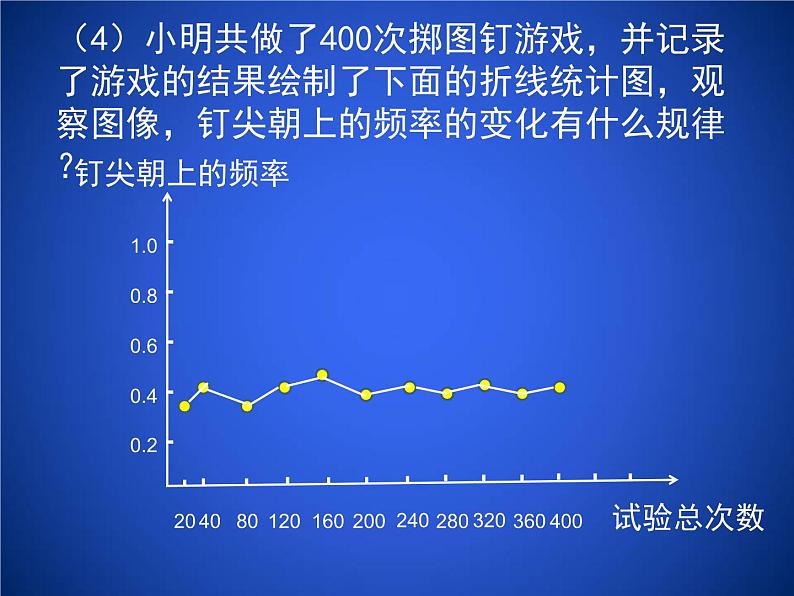
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察图像,钉尖朝上的频率的变化有什么规律?
在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)小明和小丽一起做了1000次掷图钉的试验,其中有640次钉尖朝上。据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大。你同意他们的说法吗?
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.
频率的稳定性是由瑞士数学家雅布·伯努利(1654-1705)最早阐明的,他还提出了由频率可以估计事件发生的可能性大小。
1、某射击运动员在同一条件下进行射击,结果如下表:
(1)完成上表;(2)根据上表画出该运动员击中靶心的频率的折线统计图;(3)观察画出的折线统计图,击中靶心的频率变化有什么规律?
2、某林业部门要考查某种幼树在一定条件下的移植成活率,应采用什么具体做法?
在同样条件下,大量地对这种幼树进行移植并统计成活情况,计算成活的频率.如果随着移植棵数的越来越大,频率越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值
(1)下表是统计试验中的部分数据,请补充完整:
(2)由下表可以发现,幼树移植成活的频率在____左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
(3)林业部门种植了该幼树1000棵,估计能成活_______棵.
(4)我们学校需种植这样的树苗500棵来绿化校园,则至少向林业部门购买约_______棵.
3.某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4 000名、5 000名时分别计算了各种颜色的频率,绘制折线图如下:
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
(2)你能估计调查到10000名同学时,红色的频率是多少吗?
估计调查到10000名同学时,红色的频率大约仍是40%左右.
(3)若你是该厂的负责人,你将如何安排生产各种颜色的产量?
红、黄、蓝、绿及其它颜色的生产比例大约为4:2:1:2:1 .
抛一个如图所示的瓶盖,盖口向上或盖口向下的可能性是否一样大?怎样才能验证自己结论的正确性?
1、通过本节课的学习,你了解了哪些知识?
2、在本节课的教学活动中,你获得了哪些活动体验?
抛掷一枚图钉,落地后会 出现两种情况:钉尖朝上 , 钉尖朝下。你认为钉尖朝上和 钉尖朝下的可能性一样 大吗?
小明和小丽在玩抛图钉游戏
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
频率:在n次重复试验中,不确定事件A 发生了m次,则比值 称为事件 发生的频率。
(2)累计全班同学的实验2结果,并将试验 数据汇总填入下表:
(3)根据上表完成下面的折线统计图:
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察图像,钉尖朝上的频率的变化有什么规律?
在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)小明和小丽一起做了1000次掷图钉的试验,其中有640次钉尖朝上。据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大。你同意他们的说法吗?
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.
频率的稳定性是由瑞士数学家雅布·伯努利(1654-1705)最早阐明的,他还提出了由频率可以估计事件发生的可能性大小。
1、某射击运动员在同一条件下进行射击,结果如下表:
(1)完成上表;(2)根据上表画出该运动员击中靶心的频率的折线统计图;(3)观察画出的折线统计图,击中靶心的频率变化有什么规律?
2、某林业部门要考查某种幼树在一定条件下的移植成活率,应采用什么具体做法?
在同样条件下,大量地对这种幼树进行移植并统计成活情况,计算成活的频率.如果随着移植棵数的越来越大,频率越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值
(1)下表是统计试验中的部分数据,请补充完整:
(2)由下表可以发现,幼树移植成活的频率在____左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
(3)林业部门种植了该幼树1000棵,估计能成活_______棵.
(4)我们学校需种植这样的树苗500棵来绿化校园,则至少向林业部门购买约_______棵.
3.某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4 000名、5 000名时分别计算了各种颜色的频率,绘制折线图如下:
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
(2)你能估计调查到10000名同学时,红色的频率是多少吗?
估计调查到10000名同学时,红色的频率大约仍是40%左右.
(3)若你是该厂的负责人,你将如何安排生产各种颜色的产量?
红、黄、蓝、绿及其它颜色的生产比例大约为4:2:1:2:1 .
抛一个如图所示的瓶盖,盖口向上或盖口向下的可能性是否一样大?怎样才能验证自己结论的正确性?
1、通过本节课的学习,你了解了哪些知识?
2、在本节课的教学活动中,你获得了哪些活动体验?













