初中数学北师大版七年级下册4 用尺规作角备课ppt课件

这是一份初中数学北师大版七年级下册4 用尺规作角备课ppt课件，共27页。PPT课件主要包含了同位角相等两，直线平行，②③④，两直线平，行同位角相等等内容，欢迎下载使用。

一、选择题(每题4分，共32分)
1.[2023·抚顺 母题·教材P59复习题T5]如图，直线AB，CD被 直线EF所截，AB∥CD，∠1＝122°，则∠2的度数为 (　B　)
2.如果线段AB与线段CD没有交点，则(　C　)
3.已知∠AOB，P是任意一点，过点P画一条直线与OA平 行，则这样的直线(　D　)
若点P在直线OA上，则不存在，若点P不在直线OA上， 则有一条.
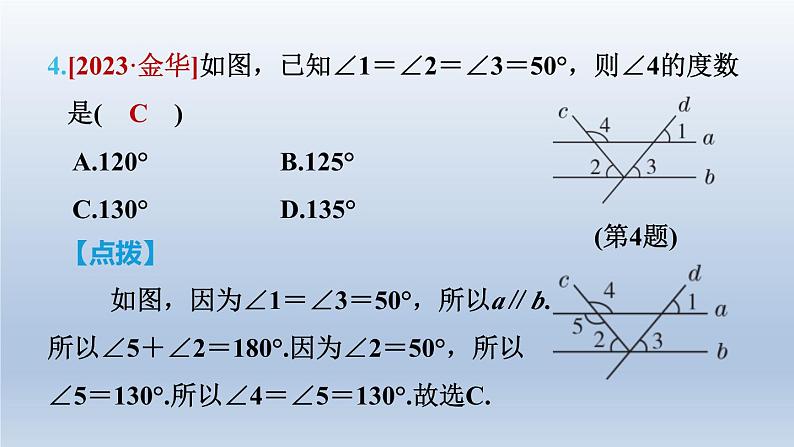
4.[2023·金华]如图，已知∠1＝∠2＝∠3＝50°，则∠4的度数 是(　C　)
如图，因为∠1＝∠3＝50°，所以a∥b.所以∠5＋∠2＝180°.因为∠2＝50°，所以∠5＝130°.所以∠4＝∠5＝130°.故选C.
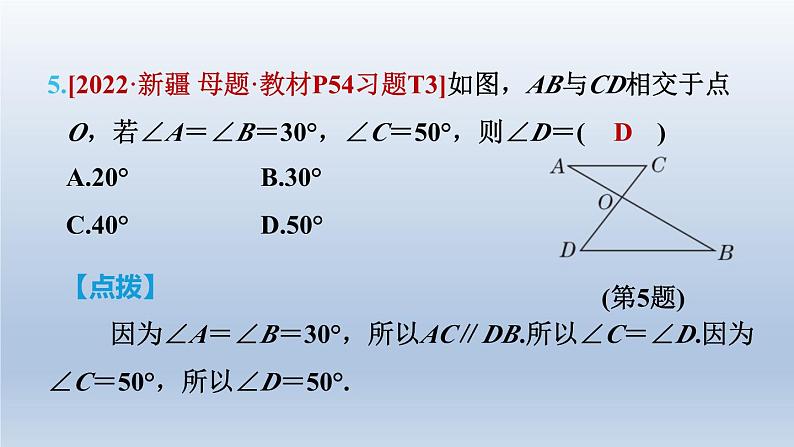
5.[2022·新疆 母题·教材P54习题T3]如图，AB与CD相交于点 O，若∠A＝∠B＝30°，∠C＝50°，则∠D＝(　D　)
因为∠A＝∠B＝30°，所以AC∥DB.所以∠C＝∠D.因为 ∠C＝50°，所以∠D＝50°.
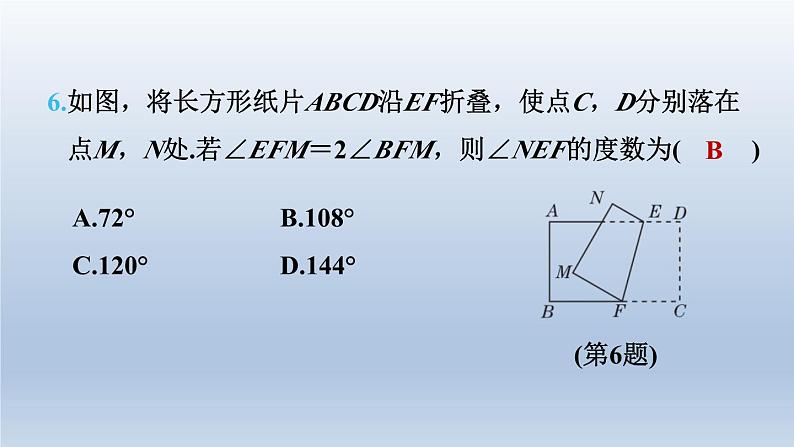
6.如图，将长方形纸片ABCD沿EF折叠，使点C，D分别落在 点M，N处.若∠EFM＝2∠BFM，则∠NEF的度数为(　B　)
7.[2023·济宁]如图，a，b是直尺的两边，a∥b，把三角尺的 直角顶点放在直尺的b边上，若∠1＝35°，则∠2的度数是 (　B　)
8.[2023·南京外国语学校期中]如图，已知AB∥CD∥EF，则 x，y，z三者之间的关系是(　B　)
根据平行线的性质可得∠CEF＝180°－y，x＝z＋ ∠CEF，利用等量代换可得x＝z＋180°－y，再变形即可.
二、填空题(每题6分，共24分)9.(母题：教材P45想一想)我们学过用直尺和三角尺画平行线 的方法，如图所示，直线a∥b的根据是 ⁠ ⁠.
同位角相等，两
10.[2023·清华附中期中]一副直角三角板如图放置，其中∠C ＝∠DFE＝90°，∠A＝45°，∠E＝60°，点D在斜边AB上. 现将三角板DEF绕着点D顺时针旋转，当DF第一次与BC 平行时，∠BDE的度数是 ⁠.
11.如图，点E在AC的延长线上，对于下列给出的四个条件： ①∠3＝∠4；②∠1＝∠2；③∠A＝∠DCE；④∠D＋ ∠ABD＝180°.能判定AB∥CD的有 (填序号).
12.[情境题 生活应用]如图为某校放置在水平操场上的篮球 架的横截面图形，初始状态时，篮球架的横梁EF平行于 AB，主柱AD垂直于地面，EF与上拉杆CF形成的角度为 ∠F，且∠F＝150°，这个篮球架可以通过调整CF和后拉 杆BC的位置来调整篮筐的高度.在调整EF的高度时，为使EF和AB平行，需要改变∠EFC和∠C的度数，调整EF使其上升到GH的位置，此时，GH与AB平行，∠CDB＝35°，并且点H，D，B在同一直线上，则∠H为 度.
如图，过点D作DI∥EF.所以∠F＋∠FDI＝180°.因为 ∠F＝150°，所以∠FDI＝180°－∠F＝30°.又因为∠FDH＝ ∠CDB＝35°，所以∠IDH＝∠FDI＋∠FDH＝30°＋35°＝ 65°.因为EF∥AB，GH∥AB，DI∥EF，所以DI∥GH.所以∠H＋∠IDH＝180°.所以∠H＝180°－∠IDH＝180°－65°＝115°.
三、解答题(共44分)13.(14分)[新趋势 学科综合]如图，水面AB与杯底CD平行， 光线EF与HI平行，FG与IJ平行.兴趣小组发现∠EFG＝ ∠HIJ.证明过程如下：
证明：∵EF∥HI，∴∠EFB＝∠HIB(依据)，∵FG∥IJ，∴∠GFB＝∠JIB，∴∠GFB＋∠EFB＝∠JIB＋∠HIB，∴∠EFG＝∠HIJ.
(1)任务一：上述材料中的“依据”指的是 ⁠ ⁠.(2)任务二：若∠FED＝65°，求∠FIH的度数.
【解】因为AB∥CD，所以∠AFE＝∠FED＝65°.因为EF∥HI，所以∠FIH＝∠AFE＝65°.
14. (14分)如图，BD⊥AC于点D，EF⊥AC于点F，∠AMD＝ ∠AGF，∠1＝∠2＝35°.(1)求∠GFC的度数.
【解】因为BD⊥AC，EF⊥AC，所以BD∥EF，∠EFC＝90°.所以∠1＝∠GFE＝35°.所以∠GFC＝35°＋90°＝125°.
(2)试说明MD∥BC.
【解】因为∠1＝∠GFE，∠1＝∠2，所以∠GFE＝∠2.所以GF∥BC.因为∠AMD＝∠AGF，所以MD∥GF.所以MD∥BC.
15.(16分)[2023·厦门一中期中]“一带一路”让中国和世界更 紧密，“中欧铁路”为了安全起见在某段铁路两旁安置了 两座可旋转探照灯.如图①所示，灯A射线从AM开始顺时 针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转 至BQ便立即回转，两灯不停交叉照射巡视.若灯A转动的 速度是每秒2度，灯B转动的速度是每秒1度.假定主道路是 平行的，即PQ∥MN，且∠BAM∶∠BAN＝2∶1.
(1)填空：∠BAN＝ ⁠°.
(2)若灯B射线先转动30秒，灯A射线才开始转动，在灯B 射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？
【解】(2)设A灯转动t秒，两灯的光束互相平行，①当0＜t＜90时，如答图①.因为PQ∥MN，所以∠PBD＝∠BDA.因为AC∥BD，所以∠CAM＝∠BDA.所以∠CAM＝∠PBD.所以2t＝1×(30＋t).解得t＝30.
②当90＜t＜150时，如答图②.因为PQ∥MN，所以∠PBD＋∠BDA＝180°.因为AC∥BD，所以∠CAN＝∠BDA.所以∠PBD＋∠CAN＝180°.所以1×(30＋t)＋(2t－180)＝180.解得t＝110.综上所述，当A灯转动30秒或110秒时，两灯的光束互相平行.
(3)如图②，若两灯同时转动，在灯A射线到达AN之前.若射出的光束交于点C，过点C作∠ACD交PQ于点D，且∠ACD＝120°，则在转动过程中，请探究∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由.
【解】(3)∠BAC和∠BCD的数量关系不会变化.理由：设灯A射线转动时间为m秒.因为∠CAN＝(180－2m)°，所以∠BAC＝60°－(180－2m)°＝(2m－120)°.又因为∠ABC＝(120－m)°，所以∠BCA＝180°－∠ABC－∠BAC＝(180－m)°，而 ∠ACD＝120°，所以∠BCD＝120°－∠BCA＝120°－(180 －m)°＝(m－60)°.所以∠BAC∶∠BCD＝2∶1.即∠BAC＝2∠BCD，所以∠BAC和∠BCD的数量关系不会变化.