2024七下数学第四章三角形全章热门考点整合应用课件（北师大版）

这是一份2024七下数学第四章三角形全章热门考点整合应用课件（北师大版），共31页。

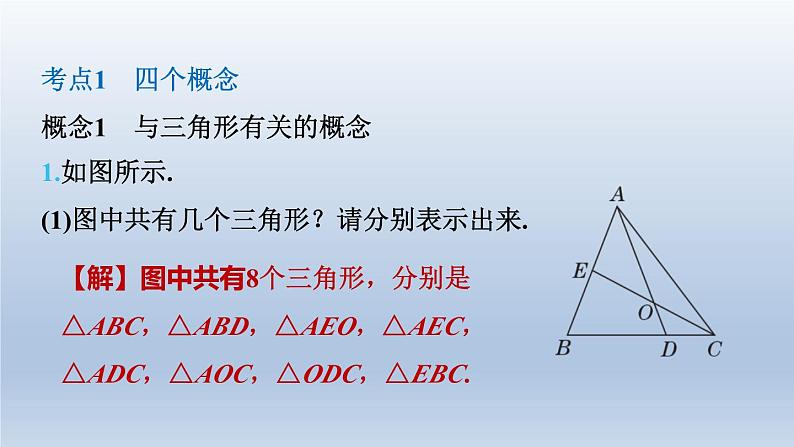
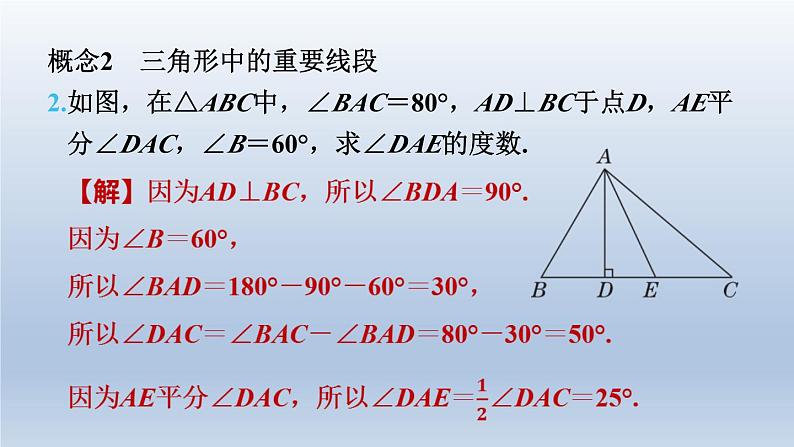
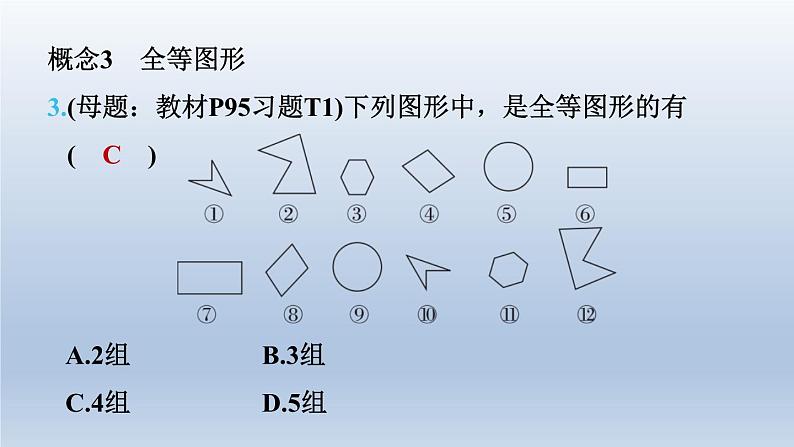
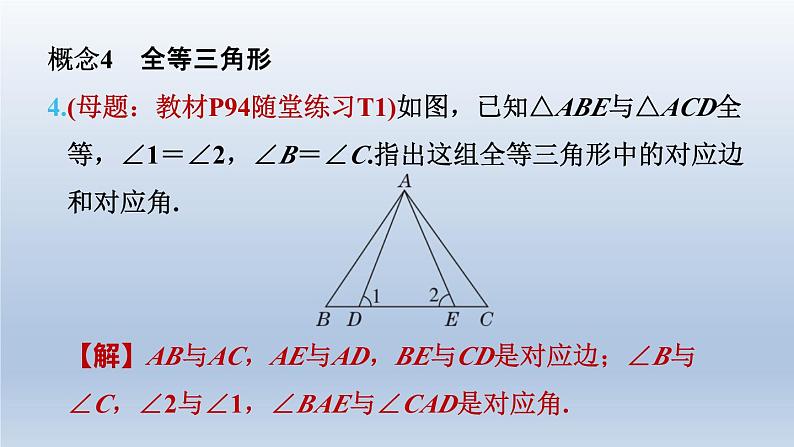
北师版七年级下第四章　三角形全章热门考点整合应用习题链接CB　　本章的主要内容有三角形及其相关概念、三角形的分类、全等三角形的判定与性质，题型涉及选择题、填空题、解答题，更多的是渗透到其他内容之中的综合性题目，是各类考试命题的重点内容.本章的考点可概括为四个概念、一个关系、两个性质、四个判定、两个技巧和两种思想.1.如图所示.(1)图中共有几个三角形？请分别表示出来.【解】图中共有8个三角形，分别是△ABC，△ABD，△AEO，△AEC，△ADC，△AOC，△ODC，△EBC.考点1　四个概念概念1　与三角形有关的概念(2)以∠AEC为内角的三角形有哪些？【解】以∠AEC为内角的三角形有△AEO，△AEC.(3)以∠ADC为内角的三角形有哪些？【解】以∠ADC为内角的三角形有△ADC，△ODC.(4)以BD为边的三角形有哪些？【解】以BD为边的三角形只有△ABD.概念2　三角形中的重要线段2.如图，在△ABC中，∠BAC＝80°，AD⊥BC于点D，AE平分∠DAC，∠B＝60°，求∠DAE的度数. 概念3　全等图形3.(母题：教材P95习题T1)下列图形中，是全等图形的有(　C　)C概念4　全等三角形4.(母题：教材P94随堂练习T1)如图，已知△ABE与△ACD全等，∠1＝∠2，∠B＝∠C.指出这组全等三角形中的对应边和对应角.【解】AB与AC，AE与AD，BE与CD是对应边；∠B与∠C，∠2与∠1，∠BAE与∠CAD是对应角.考点2　一个关系——三角形的三边关系5.[情境题 游戏活动型]如图，第二次龟兔赛跑时，聪明的乌龟设计的比赛规则是从A点跑到B点，因A，B之间有猎人的陷阱，乌龟让兔子沿路线A→C→B前进，而它沿路线A→D→E→B前进.乌龟告诉兔子说，兔子只跑三角形的两边(AC＋CB)，而它要跑四边形的三边(AD＋DE＋EB)，这样自己跑的路程比兔子跑的路程长，请你用所学的知识说明它们谁跑的路程长.【解】如图，设直线DE交AC于点M，交BC于点N.在△ADM中，AM＋MD＞AD.在△CMN中，CM＋CN＞MN，即CM＋CN＞MD＋DE＋NE.在△BNE中，BN＋NE＞BE，所以AM＋MD＋CM＋CN＋BN＋NE＞AD＋MD＋DE＋NE＋BE，所以AM＋CM＋CN＋BN＞AD＋DE＋BE，即AC＋CB＞AD＋DE＋BE，所以兔子跑的路程长.考点　两个性质性质1　三角形内角和的性质6.[2023·东营]如图，AB∥CD，点E在线段BC上(不与点B，C重合)，连接DE，若∠D＝40°，∠BED＝60°，则∠B＝(　B　)B性质2　全等三角形的性质7.如图，在Rt△ABC中，∠ACB＝90°，且AC＝BC＝4 cm.已知△BCD≌△ACE，求四边形AECD的面积. 考点4　四个判定判定1　SSS8.如图，已知AB＝DC，AD＝BC，O是DB的中点，过点O的直线分别交DA和BC的延长线于点E，F.试说明：∠E＝∠F. 判定2　ASA9.[2022·衢州]如图，已知∠1＝∠2，∠3＝∠4.试说明：AB＝AD. 10.[2023·温州八中模拟]如图，在△ABC和△ECD中，∠ABC＝∠EDC＝90°，B为CE中点，BC＝CD.(1)试说明：△ABC≌△EDC；【解】因为∠ABC＝∠EDC＝90°，BC＝DC，∠C＝∠C，所以△ABC≌△EDC(ASA).(2)若CD＝2，求AC的长.【解】因为CD＝2，△ABC≌△EDC，所以BC＝CD＝2，AC＝CE.因为B为CE中点，所以BE＝BC＝2，所以CE＝4，所以AC＝4.判定3　AAS11.[2023·乐山]如图，已知AB与CD相交于点O，AC∥BD，AO＝BO，试说明：AC＝BD. 判定4　SAS12.[2023·天津一中期末]如图，点E，F在BC上，BE＝CF，AB＝DC，∠B＝∠C，试说明：AF＝DE. 考点5　两个技巧技巧1　说明线段数量关系的方法13.如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，∠ABC的平分线交AC于点D，过点C作BD的垂线交BD的延长线于点E，交BA的延长线于点F.试说明：【解】因为BE平分∠ABC，所以∠FBE＝∠CBE.因为CE⊥BE，所以∠FEB＝∠CEB＝90°.又因为BE＝BE，所以△FBE≌△CBE(ASA)，所以BF＝BC.(1)BF＝BC；(2)BD＝2CE.【解】因为∠BAC＝∠FAC＝∠FEB＝90°，所以∠ABD＋∠F＝∠ACF＋∠F＝90°，所以∠ABD＝∠ACF.又因为AB＝AC，∠BAD＝∠CAF，所以△BDA≌△CFA(ASA)，所以BD＝CF.又因为△FBE≌△CBE，所以EF＝EC，即CF＝2EC，所以BD＝2CE.技巧2　添加辅助线的方法14.如图，AB＝DC，∠A＝∠D.试说明：∠ABC＝∠DCB.【解】如图，分别取AD，BC的中点N，M，连接BN，CN，MN，则有AN＝DN，BM＝CM. 所以△ABN≌△DCN(SAS)，所以∠ABN＝∠DCN，NB＝NC. 所以△NBM≌△NCM(SSS)，所以∠NBM＝∠NCM，所以∠NBM＋∠ABN＝∠NCM＋∠DCN，即∠ABC＝∠DCB.考点6　两种思想思想1　方程思想15.如图，在△ABC中，∠BAC＝4∠ABC＝4∠C，BD⊥CA交CA的延长线于点D，求∠ABD的度数.【解】设∠C＝x°，则∠ABC＝x°，∠BAC＝4x°.在△ABC中，x＋x＋4x＝180，解得x＝30.所以∠BAC＝120°，所以∠DAB＝60°.因为BD⊥AC，所以∠ABD＝90°－∠DAB＝90°－60°＝30°.思想2　转化思想16.农科所有一块五边形的试验田如图所示，已知在五边形ABCDE中，∠ABC＝∠AED＝90°，AB＝CD＝AE＝BC＋DE＝20 m，求这块试验田的面积.【解】如图，延长DE至点F，使EF＝BC，连接AC，AD，AF，易得CD＝FD. 所以△ABC≌△AEF(SAS)，所以AC＝AF. 所以△ACD≌△AFD(SSS).