北师大版七年级下册2 探索轴对称的性质课堂教学ppt课件

这是一份北师大版七年级下册2 探索轴对称的性质课堂教学ppt课件，共27页。PPT课件主要包含了应用实际，拓展提升等内容，欢迎下载使用。
1.轴对称图形和成轴对称的性质中关键有两点：一是对应图 形的全等性，根据全等的性质可得到对应的边、角相等；二 是对称轴的垂直平分性，揭示对称轴与对应点所连线段之间 的位置关系.2.画与已知图形成轴对称的图形的方法：(1)确定原图形的关 键点； (2)作出每个关键点关于对称轴对称的对应点；(3)按 原图形的顺序依次连接相应的对称点.
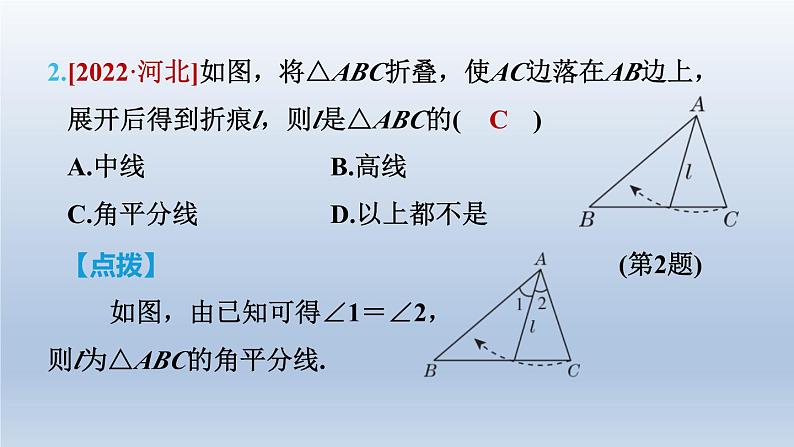
知识点1　轴对称及轴对称图形的对应角性质
1.如图，∠A＝30°，∠C'＝60°，△ABC与△A'B'C'关于直线l 对称，则∠B的度数为(　C　)
2.[2022·河北]如图，将△ABC折叠，使AC边落在AB边上， 展开后得到折痕l，则l是△ABC的(　C　)
如图，由已知可得∠1＝∠2，则l为△ABC的角平分线.
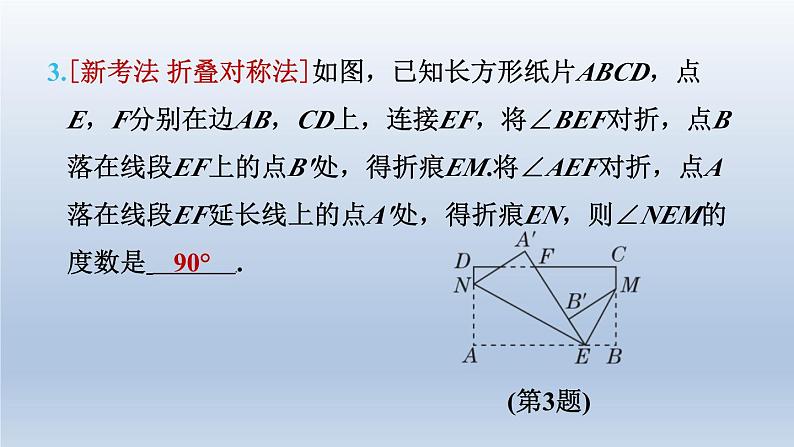
3.[新考法 折叠对称法]如图，已知长方形纸片ABCD，点 E，F分别在边AB，CD上，连接EF，将∠BEF对折，点B 落在线段EF上的点B'处，得折痕EM.将∠AEF对折，点A 落在线段EF延长线上的点A'处，得折痕EN，则∠NEM的 度数是 ⁠.
由题意得，∠AEA'＝2∠A'EN，∠BEA'＝2∠B'EM.因 为∠AEA'＋∠BEA'＝180°，即2∠A'EN＋2∠B'EM＝ 2(∠A'EN＋∠B'EM)＝2∠NEM＝180°，所以∠NEM＝90°.
知识点2　轴对称及轴对称图形的对应边性质
4.(母题：教材P118做一做)如图，若△ABC与△A'B'C'关于直 线MN对称，BB'交MN于点O，则下列结论中不一定正确的 是(　B　)
5.[2023·天津一中月考]如图，将一张三角形纸片ABC沿过点 B的直线折叠，使点C落在AB边上的点E处，折痕为BD， 则下列结论一定正确的是(　D　)
根据折叠易知，四边形BCDE是轴对称轴图形，对称轴 是BD.先根据轴对称图形的性质得出BE＝BC，再根据AE＋ BE＝AB及等量代换可得答案.
6.[2022·六盘水]如图，将一张长方形纸对折，再对折，然后 沿图中虚线剪下，剪下的图形展开后可得到(　C　)
知识点3　画轴对称图形或轴对称7.(母题：教材P119做一做)下列图形均是以直线l为对称轴所 作的轴对称图形，其中错误的是(　C　)
8.如图，在小方格中画与△ABC成轴对称的三角形(不与 △ABC重合)，这样的三角形有(　C　)
如图，可以选择的对称轴有EF，CG，AH，所以与 △ABC成轴对称的三角形能画出3个.
易错点　弄错相等线段或角
9.如图，△ABC与△ADC关于AC对称，则下面结论错误的是 (　D　)
因为△ABC与△ADC关于AC对称，所以AC平分 ∠BAD，CA平分∠BCD，BD⊥AC，AC平分线段BD.故A， B，C选项正确，故选D.
思维发散练1　利用轴对称的性质求边和角10.如图，点P在∠AOB的内部，点M，N分别是点P关于直线 OA，OB的对称点，线段MN分别交OA，OB于点E，F.(1)若MN＝20 cm，求△PEF的周长；
【解】△PEF的周长是20 cm.
【解】如图，设MP与OA相交于点R， PN与OB相交于点T.由(1)知ME＝PE，NF＝PF，易得∠M＝∠EPM，∠N＝∠FPN，所以∠PEF＝180°－∠PEM＝∠M＋ ∠EPM＝2∠M.同理可得∠PFE＝2∠N.
(2)若∠AOB＝35°，求∠EPF的度数.(提示：四边形的内角和为360°)
由题知∠PRE＝∠PTF＝90°，所以在四边形OTPR中，∠MPN＋∠AOB＝180°.因为∠MPN＋∠M＋∠N＝180°，所以∠M＋∠N＝∠AOB＝35°.所以∠EPF＝180°－(∠PEF＋∠PFE)＝180°－2(∠M＋ ∠N)＝180°－35°×2＝110°.
思维发散练2　利用画轴对称确定最短距离的点11.(1)如图，一条笔直的河流l的同侧有A，B两个村庄，要把 A村的产品运往B村，按计划要先到河岸M处接一批货 物，然后一起运往B村.要使总路程最短，点M应选在河流l 的什么位置？
【解】(1)如图①，根据轴对称的性质和“两点之间线段最短”，可知作点A关于河流l的对称点A'，连接A'B，交河流l于点M，则点M即为所求.
(2)在(1)的条件下，若在河岸M处接货后，需沿河岸行a km至N处，再将货物运送至B村.要使总路程最短，则M， N两点应选在河流l的什么位置？
【解】如图②，过点A作AE∥l， 在射线AE上截取AA'＝a km；作点B关 于河流l的对称点B'，连接A'B'交河流l 于点N；在河流l上点N的左侧截取NM ＝a km，则M，N两点即为所求.
命题新趋势　利用轴对称的性质探求新定义中的角度12.[新考法 阅读新定义法] [定义]如图①，OM平分∠AOB， 则称射线OB，OA关于OM对称.[理解题意]
(1)如图①，射线OB，OA关于OM对称且∠AOB＝45°，则 ∠AOM＝ °；
(2)如图②，若∠AOB＝45°，OP在∠AOB内部，OP，OP1关 于OB对称，OP，OP2关于OA对称，求∠P1OP2的度数；
【解】因为OP，OP1关于OB对称，所以∠POP1＝2∠BOP.又因为OP，OP2关于OA对称，所以∠POP2＝2∠AOP.因为∠P1OP2＝∠POP1＋∠POP2，所以∠P1OP2＝2∠BOP＋2∠AOP＝2∠AOB＝90°.
(3)如图③，若∠AOB＝45°，OP在∠AOB外部，且0°＜ ∠AOP＜45°，OP，OP1关于OB对称，OP，OP2关于OA对 称，求∠P1OP2的度数；
【解】因为OP，OP1关于OB对称，所以∠POP1＝2∠BOP.又因为OP，OP2关于OA对称，所以∠POP2＝2∠AOP.因为∠P1OP2＝∠POP1－∠POP2，所以∠P1OP2＝2∠BOP－2∠AOP＝2∠AOB＝90°.
(4)如图④，若∠AOB＝45°，OP，OP1关于∠AOB的OB边对 称，∠AOP1＝4∠BOP1，求∠AOP的度数.(直接写出答案)
【解】∠AOP＝30°或54°.
①当OP在∠AOB内部时，如图①，因为OP，OP1关于 OB对称，所以∠BOP＝∠BOP1.因为∠AOP1＝4∠BOP1，所 以∠AOB＝3∠BOP1＝45°，所以∠BOP1＝15°，所以∠BOP ＝∠BOP1＝15°，所以∠AOP＝45°－15°＝30°.
②当OP在∠AOB外部时，因为∠AOP1＝4∠BOP1，所以射线OP在射线OB的上方，如图②.因为OP，OP1关于∠AOB的 OB边对称，所以∠BOP＝∠BOP1.因为∠AOP1＝4∠BOP1， 所以∠AOB＝∠BOP1＋∠AOP1＝5∠BOP1＝45°，所以 ∠BOP1＝9°，所以∠BOP＝∠BOP1＝9°，所以∠AOP＝45°＋9°＝54°.综上所述，∠AOP的度数为30°或54°.