北师大版2 探索轴对称的性质背景图ppt课件

这是一份北师大版2 探索轴对称的性质背景图ppt课件，共25页。PPT课件主要包含了1求BC的长等内容，欢迎下载使用。
　　本部分内容的考点主要如下：(1)轴对称图形的识别，近 几年中考常以交通标志图案、汽车标志图案、学习工具等为 背景材料进行命题，考查轴对称图形的识别的题目为基础 题，题型主要是选择题； (2)轴对称的性质及线段的垂直平 分线，近几年中考常将线段的垂直平分线与其他知识综合在 一起考查，若单独考查，常与三角形的周长有关，题目难度 不大，题型主要是选择题和填空题.
应用1　轴对称图形及成轴对称的定义在识别中的应用1.[2023·和衡阳 新趋势·学科综合]下列四种化学仪器的示意 图是轴对称图形的是(　C　)
2.(母题：教材P119随堂练习)如图，△ABC与△ADE关于直 线MN对称，BC与DE的交点F在直线MN上.(1)指出图中的两组对称点；
【解】B和D，C和E.(答案不唯一)
(2)指出图中相等的线段；
【解】AC和AE，AB和AD，BC和DE，BF和DF，CF和EF.
(3)指出图中其他关于直线MN对称的三角形.
【解】△AFB和△AFD，△AEF和△ACF.
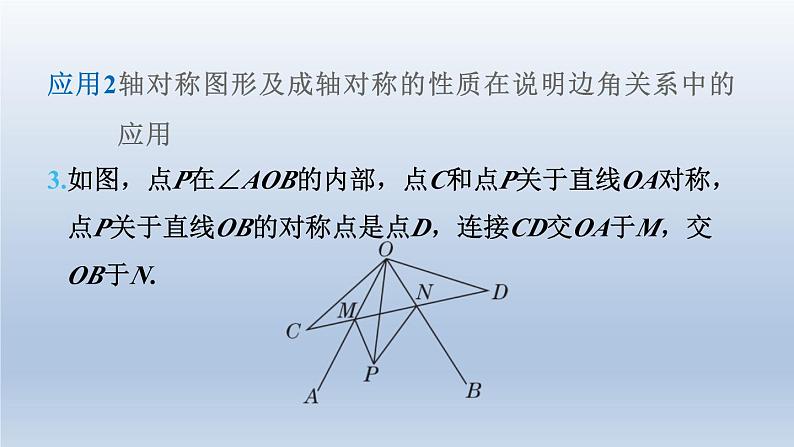
应用2轴对称图形及成轴对称的性质在说明边角关系中的 应用3.如图，点P在∠AOB的内部，点C和点P关于直线OA对称， 点P关于直线OB的对称点是点D，连接CD交OA于M，交 OB于N.
(1)①若∠AOB＝60°，则∠COD＝ ⁠；
因为点C和点P关于直线OA对称，所以∠AOC＝∠AOP. 因为点P关于直线OB的对称点是点D，所以∠BOD＝ ∠BOP，所以∠COD＝∠AOC＋∠AOP＋∠BOP＋∠BOD＝ 2(∠AOP＋∠BOP)＝2∠AOB＝2×60°＝120°.
(1) ②若∠AOB＝α，求∠COD的度数；
【解】因为点C和点P关于直线OA对称，所以∠AOC＝∠AOP.因为点P关于直线OB的对称点是点D，所以∠BOD＝∠BOP，所以∠COD＝∠AOC＋∠AOP＋ ∠BOP＋∠BOD＝2(∠AOP＋∠BOP)＝2∠AOB＝2α.
根据轴对称的性质，可知CM＝PM，DN＝PN，所以 △PMN的周长为PM＋PN＋MN＝CM＋DN＋MN＝CD＝4.
(2)若CD＝4，则△PMN的周长为 ⁠.
应用3　轴对称的性质在作图中的应用4.在下面的三个网格中均有三个阴影小正方形，请你在这三 个网格图中各补涂出一个有阴影小正方形，使补涂后的图 形(阴影部分)为轴对称图形.
【解】如图所示.(答案不唯一)
5.图①、图②、图③都是3×3的正方形网格，每个小正方形 的顶点称为格点.A，B，C均为格点，在给定的网格中，按 下列要求画图：(1)在图①中，画一条不与AB重合的线段MN，使MN与AB 关于某条直线对称，且M，N为格点；
【解】如图①，MN即为所求.(答案不唯一)
(2)在图②中，画一条不与AC重合的线段PQ，使PQ与AC关 于某条直线对称，且P，Q为格点；
【解】如图②，PQ即为所求.(答案不唯一)
(3)在图③中，画一个△DEF，使△DEF与△ABC关于某条 直线对称，且D，E，F为格点.
【解】如图③，△DEF即为所求.(答案不唯一)
应用4　轴对称的性质在辨析中的应用6.如图，O为△ABC内部一点，OB＝3，P，R分别为点O关于直线AB，BC的对称点.(1)请指出当∠ABC为多少度时，会使得PR的长度等于6，并说明理由.
【解】(1)当∠ABC＝90°时，PR＝6.理由：如图，连接OP，OR，PB，RB.因为P，R分别为点O关于直线AB，BC 的对称点，所以PB＝OB＝3，RB＝OB ＝3，∠ABP＝∠ABO，∠CBR＝∠CBO.
因为∠ABC＝90°，所以∠ABP＋∠CBR＝∠ABO＋∠CBO＝∠ABC＝90°，所以∠PBR＝180°，所以点P，B，R共线，所以PR＝PB＋RB＝6.
(2)根据第(1)问，请判断当∠ABC不是你指出的角度时，PR的长度是小于6还是大于6？并说明理由.
【解】PR的长度小于6.理由：因为∠ABC≠90°，所以点P，B，R不在同一条直线上，所以PR＜PB＋BR.因为PB＋BR＝3＋3＝6，所以PR＜6.
应用5　轴对称的性质在折叠中的应用7.[2023·深圳光明中学期中]如图①是长方形纸带，∠DEF＝ 26°，将纸带沿EF折叠成图②，再沿BF折叠成图③，则图 ③中的∠CFE＝ 度.
因为四边形ABCD是长方形，所以AD∥BC，所以 ∠BFE＝∠DEF＝26°.在图②中，∠EFG＝26°，∠EFG处重 叠了2层，在图③中，∠EFG＝26°，∠EFG处重叠了3层， 所以∠CFE＝∠CFG－∠EFG＝180°－2∠BFE－∠EFG＝ 180°－3×26°＝102°.
应用6　构造轴对称在解题中的应用
8.如图，在△ABC中，AB边的垂直平分线l1交BC于点D，AC 边的垂直平分线l2交BC于点E，l1与l2相交于点O，△ADE 的周长为6 cm.
【解】如图，设直线l1与AB的交点为M.因为l1是AB边的垂直平分线，所以AM＝BM，∠AMD＝∠BMD.又因为DM＝DM，所以△AMD≌△BMD(SAS)，所以AD＝BD.同理可得AE＝CE.
所以AD＋DE＋AE＝BD＋DE＋CE＝BC.因为△ADE的周长为6 cm，即AD＋DE＋AE＝6 cm，所以BC＝6 cm.
(2)连接OA，OB，OC，若△OBC的周长为16 cm，求OA的长.
【解】因为l1是AB边的垂直平分线，l2是AC边的垂直平分线，l1与l2相交于点O，所以OB＝OA＝OC.因为△OBC的周长为16 cm，即OC＋OB＋BC＝16 cm，所以OC＋OB＝16－6＝10(cm).所以OB＝OC＝5 cm，所以OA＝5 cm.
9.如图，在△ABC中，AB＝AC，D，E是BC边上的点，连接 AD，AE，以△ADE的边AE所在直线为对称轴作与△ADE 成轴对称的图形△AD'E，连接D'C，BD＝CD'.
(1)试说明：△ABD≌△ACD'；