




还剩10页未读,
继续阅读
所属成套资源:2024北师大版七年级下册数学整册课件多份
成套系列资料,整套一键下载
2024七下数学极速提分法第9招用全等三角形说明五种常见结论的技巧课件(北师大版)
展开
这是一份2024七下数学极速提分法第9招用全等三角形说明五种常见结论的技巧课件(北师大版),共18页。
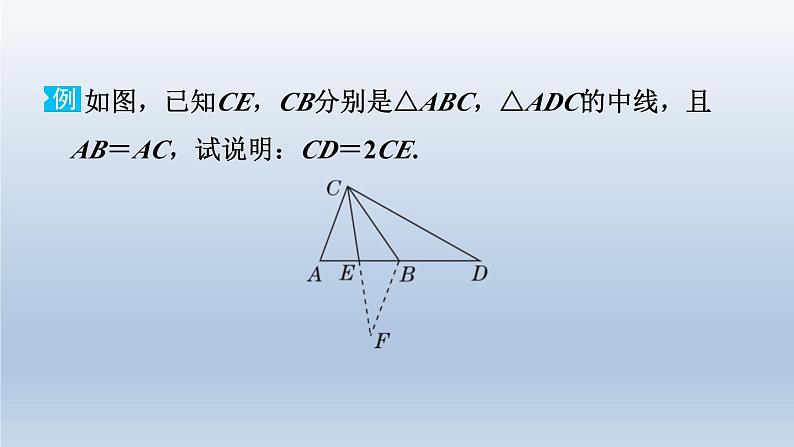
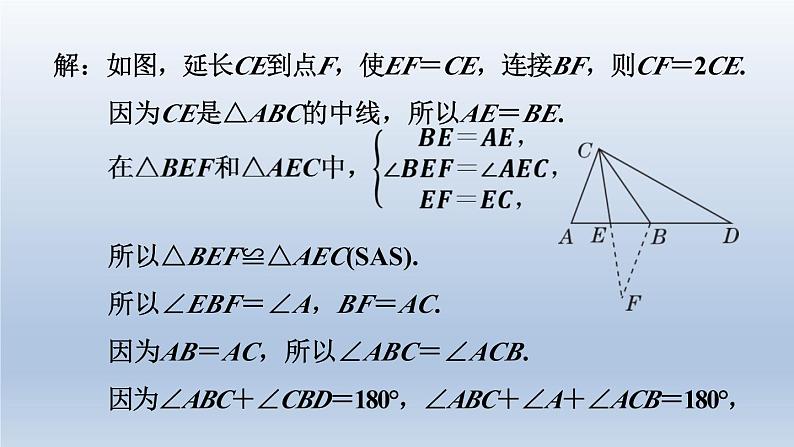
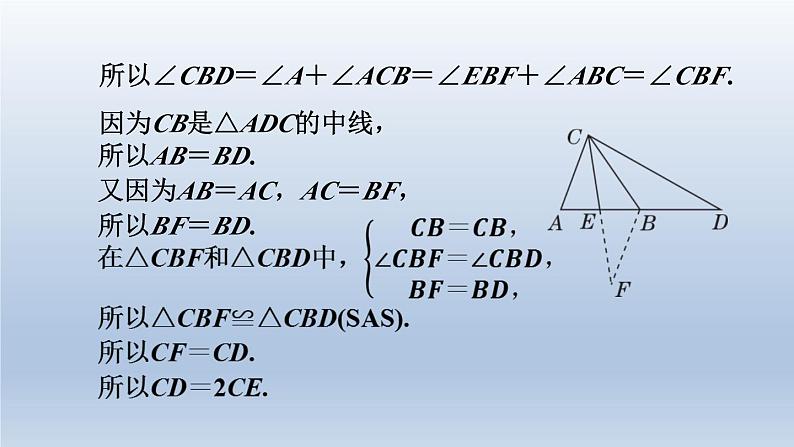
北师版七年级下第9招 用全等三角形说明五种常见结论的技巧全等三角形是说明线段或角相关结论的重要方法之一,其思 路如下:1.观察要说明的相关结论涉及的线段或角(用等量代换后的线 段或角)在哪两个可能全等的三角形之中;2.分析要说明全等的这两个三角形,已知什么条件,还缺什 么条件;3.设法推出所缺条件;4.利用三角形全等得到线段或角相等.当待说明的相关结论涉及的线段或角分布在两个不全等三 角形中(也找不到等量代换)时,常需添加辅助线构造出全 等三角形,使它们分别包括一个所要说明的相关结论涉及 的线段或角. 如图,已知CE,CB分别是△ABC,△ADC的中线,且 AB=AC,试说明:CD=2CE. 倍长中线法是说明一条线段长是另一条线段长的2 倍的常用方法之一,它将说明线段的倍数关系转化为说明线段的相等关系,构造全等三角形,利用全等三角形对应边相等进行说明.本例中将CE延长一倍至点F,连接BF,可构造△ACE和△BFE全等,这样就出现了与2CE长度相等的线段,又为△CBD和△CBF全等创造了条件.解:如图,延长CE到点F,使EF=CE,连接BF,则CF=2CE.因为CE是△ABC的中线,所以AE=BE. 所以△BEF≌△AEC(SAS).所以∠EBF=∠A,BF=AC.因为AB=AC,所以∠ABC=∠ACB.因为∠ABC+∠CBD=180°,∠ABC+∠A+∠ACB=180°,所以∠CBD=∠A+∠ACB=∠EBF+∠ABC=∠CBF.因为CB是△ADC的中线,所以AB=BD.又因为AB=AC,AC=BF,所以BF=BD. 运用全等三角形法说明线段相等1.[2023·天津一中期末]如图,在五边形ABCDE中,∠BCD= ∠EDC=90°,BC=ED,AC=AD.试说明:AB=AE. 运用全等三角形法说明线段的数量关系2.在△ABC中,AB=AC,∠A=36°,CD平分∠ACB交AB于 点D,E,F分别在AC,BC上,且∠EDF=108°.(1)求∠ADC的度数; 所以∠ADC=180°-(∠A+∠ACD)=180°-(36°+36°)=108°.(2)试说明:AE+BF=BC.【解】由(1)得∠ACD=∠BCD=36°=∠A,∠ADC=108°,易知AD=CD.因为∠EDF=108°,所以∠ADC=∠EDF. 所以∠ADE=∠CDF. 运用等线段代换法说明线段的和差关系3.如图,在△ABC中,AC=BC,∠ACB=90°,D为BC延长 线上一点,BF⊥AD于点F,交AC于点E. (1)试说明:BE=AD;(2)过点C作CM∥AB交AD于点M,连接EM,试说明:BE =AM+EM.【解】因为△CBE≌△CAD,所以CE=CD.因为AC=BC,∠ACB=90°,所以∠ABC=45°.因为CM∥AB,所以∠DCM=∠ABC=45°.所以∠ACM=45°.所以∠DCM=∠ECM. 运用截长补短法说明线段的和差关系4.如图,在四边形ABDE中,C是BD边的中点.若AC平分 ∠BAE,∠ACE=90°,猜想线段AE,AB,DE满足的数量 关系,并说明理由.【解】AE=AB+DE.理由:如图,在AE上截取AF=AB,连接CF.因为AC平分∠BAE,所以∠BAC=∠FAC.又因为AC=AC,所以△BAC≌△FAC(SAS).所以BC=FC,∠ACB=∠ACF.因为∠ACE=90°,所以∠ACF+∠FCE=90°,∠ACB+∠DCE=90°.所以∠FCE=∠DCE.因为C为BD边的中点,所以BC=DC. 所以DC=FC.又因为CE=CE,所以△FCE≌△DCE(SAS).所以DE=FE.所以AE=AF+FE=AB+DE. 运用倍长中线法说明三边关系 【解】如图,延长AD至点E,使DE=AD,连接BE.因为AD是BC边上的中线,所以CD=BD. 所以△ACD≌△EBD(SAS).所以AC=EB.在△ABE中,AB-BE<AE<AB+BE,即AB-AC<2AD<AB+AC,
北师版七年级下第9招 用全等三角形说明五种常见结论的技巧全等三角形是说明线段或角相关结论的重要方法之一,其思 路如下:1.观察要说明的相关结论涉及的线段或角(用等量代换后的线 段或角)在哪两个可能全等的三角形之中;2.分析要说明全等的这两个三角形,已知什么条件,还缺什 么条件;3.设法推出所缺条件;4.利用三角形全等得到线段或角相等.当待说明的相关结论涉及的线段或角分布在两个不全等三 角形中(也找不到等量代换)时,常需添加辅助线构造出全 等三角形,使它们分别包括一个所要说明的相关结论涉及 的线段或角. 如图,已知CE,CB分别是△ABC,△ADC的中线,且 AB=AC,试说明:CD=2CE. 倍长中线法是说明一条线段长是另一条线段长的2 倍的常用方法之一,它将说明线段的倍数关系转化为说明线段的相等关系,构造全等三角形,利用全等三角形对应边相等进行说明.本例中将CE延长一倍至点F,连接BF,可构造△ACE和△BFE全等,这样就出现了与2CE长度相等的线段,又为△CBD和△CBF全等创造了条件.解:如图,延长CE到点F,使EF=CE,连接BF,则CF=2CE.因为CE是△ABC的中线,所以AE=BE. 所以△BEF≌△AEC(SAS).所以∠EBF=∠A,BF=AC.因为AB=AC,所以∠ABC=∠ACB.因为∠ABC+∠CBD=180°,∠ABC+∠A+∠ACB=180°,所以∠CBD=∠A+∠ACB=∠EBF+∠ABC=∠CBF.因为CB是△ADC的中线,所以AB=BD.又因为AB=AC,AC=BF,所以BF=BD. 运用全等三角形法说明线段相等1.[2023·天津一中期末]如图,在五边形ABCDE中,∠BCD= ∠EDC=90°,BC=ED,AC=AD.试说明:AB=AE. 运用全等三角形法说明线段的数量关系2.在△ABC中,AB=AC,∠A=36°,CD平分∠ACB交AB于 点D,E,F分别在AC,BC上,且∠EDF=108°.(1)求∠ADC的度数; 所以∠ADC=180°-(∠A+∠ACD)=180°-(36°+36°)=108°.(2)试说明:AE+BF=BC.【解】由(1)得∠ACD=∠BCD=36°=∠A,∠ADC=108°,易知AD=CD.因为∠EDF=108°,所以∠ADC=∠EDF. 所以∠ADE=∠CDF. 运用等线段代换法说明线段的和差关系3.如图,在△ABC中,AC=BC,∠ACB=90°,D为BC延长 线上一点,BF⊥AD于点F,交AC于点E. (1)试说明:BE=AD;(2)过点C作CM∥AB交AD于点M,连接EM,试说明:BE =AM+EM.【解】因为△CBE≌△CAD,所以CE=CD.因为AC=BC,∠ACB=90°,所以∠ABC=45°.因为CM∥AB,所以∠DCM=∠ABC=45°.所以∠ACM=45°.所以∠DCM=∠ECM. 运用截长补短法说明线段的和差关系4.如图,在四边形ABDE中,C是BD边的中点.若AC平分 ∠BAE,∠ACE=90°,猜想线段AE,AB,DE满足的数量 关系,并说明理由.【解】AE=AB+DE.理由:如图,在AE上截取AF=AB,连接CF.因为AC平分∠BAE,所以∠BAC=∠FAC.又因为AC=AC,所以△BAC≌△FAC(SAS).所以BC=FC,∠ACB=∠ACF.因为∠ACE=90°,所以∠ACF+∠FCE=90°,∠ACB+∠DCE=90°.所以∠FCE=∠DCE.因为C为BD边的中点,所以BC=DC. 所以DC=FC.又因为CE=CE,所以△FCE≌△DCE(SAS).所以DE=FE.所以AE=AF+FE=AB+DE. 运用倍长中线法说明三边关系 【解】如图,延长AD至点E,使DE=AD,连接BE.因为AD是BC边上的中线,所以CD=BD. 所以△ACD≌△EBD(SAS).所以AC=EB.在△ABE中,AB-BE<AE<AB+BE,即AB-AC<2AD<AB+AC,
相关资料
更多









