2024七下数学极速提分法第4招与相交线平行线相关的四类角的计算课件（北师大版）

这是一份2024七下数学极速提分法第4招与相交线平行线相关的四类角的计算课件（北师大版），共13页。

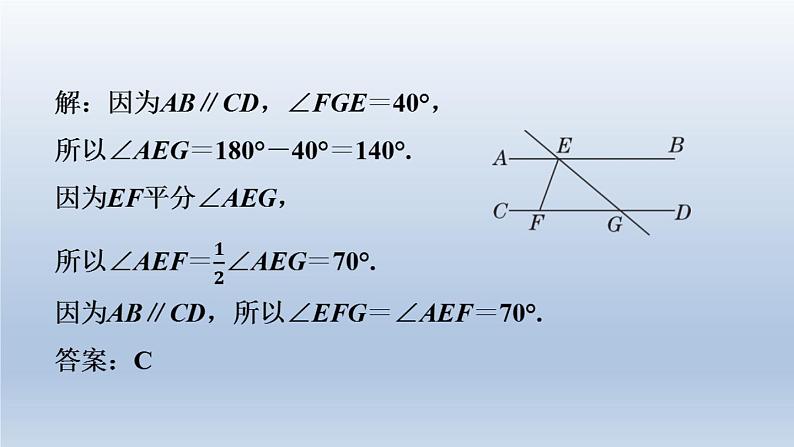
北师版七年级下第4招　与相交线、平行线相关的四类角的计算与相交线、平行线相关的角的计算大致有两类呈现形式，一类是利用余角、补角、对顶角、角平分线等进行相关的计算，另一类是利用平行线的性质和判定进行相关的计算. 如图，AB∥CD，EF平分∠AEG，如果∠FGE＝40°，那么∠EFG的度数为(　　) 看清楚∠FGE与∠AEG是同旁内角关系，从而确定互补关系；再根据角平分线的定义求出∠AEF的度数，由AB∥CD得∠EFG＝∠AEF，问题即可获得解决.  通过平角、对顶角转换求角的度数1.如图，已知直线AB，CD相交于点O，OA平分∠EOC，若∠EOC∶∠EOD＝2∶3，求∠BOD的度数.解：由∠EOC∶∠EOD＝2∶3，设∠EOC＝2x°，则∠EOD＝3x°.因为∠EOC＋∠ ＝180°( )，所以2x＋3x＝180，解得x＝36.EOD平角的定义 对顶角相等　36°　 利用垂直求角的度数2.如图，两直线AB，CD相交于点O，OE平分∠BOD，∠AOC∶∠AOD＝7∶11.(1)∠COE的度数为 ⁠；145°　【点拨】 (2)若OF⊥OE，求∠COF的度数.【解】因为OF⊥OE，所以∠FOE＝90°.由(1)知∠DOE＝35°，所以∠FOD＝90°－∠DOE＝90°－35°＝55°.所以∠COF＝180°－∠FOD＝180°－55°＝125°. 利用平行线的性质求角的度数3.[2023·营口]如图，AD是∠EAC的平分线，AD∥BC，∠BAC＝100°，则∠C的度数是(　B　)B 综合应用平行线的性质与判定求角度4.[2023·长沙长郡双语实验中学期中]如图，DE∥BC，BD平分∠ABC，EF平分∠AED.(1)试说明：EF∥BD；  (2)若BD⊥AC，∠C＝2∠2，求∠A的度数.所以∠C＝2∠CBD.所以∠CBD＋2∠CBD＝90°.解得∠CBD＝30°.所以∠C＝60°，∠ABC＝60°.所以∠A＝180°－∠ABC－∠C＝60°.