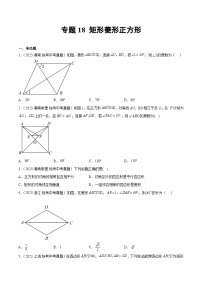
2022年中考数学真题考点分类专题汇编(全国通用)专题18矩形菱形正方形(共49题)【原卷版+解析】
展开1.(2022•陕西)在下列条件中,能够判定▱ABCD为矩形的是( )
A.AB=ADB.AC⊥BDC.AB=ACD.AC=BD
2.(2022•株洲)如图所示,在菱形ABCD中,对角线AC与BD相交于点O,过点C作CE∥BD交AB的延长线于点E,下列结论不一定正确的是( )
A.OB=CEB.△ACE是直角三角形
C.BC=AED.BE=CE
3.(2022•宁波)将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
A.正方形纸片的面积B.四边形EFGH的面积
C.△BEF的面积D.△AEH的面积
4.(2022•安徽)两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α﹣90°B.α﹣45°C.180°﹣αD.270°﹣α
5.(2022•滨州)下列命题,其中是真命题的是( )
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
6.(2022•绍兴)如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,边BC上的动点.下列四种说法:
①存在无数个平行四边形MENF;
②存在无数个矩形MENF;
③存在无数个菱形MENF;
④存在无数个正方形MENF.
其中正确的个数是( )
A.1B.2C.3D.4
7.(2022•重庆)如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( )
A.45°B.60°C.67.5°D.77.5°
8.(2022•重庆)如图,在正方形ABCD中,对角线AC、BD相交于点O.E、F分别为AC、BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为( )
A.50°B.55°C.65°D.70°
9.(2022•泸州)如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为( )
A.B.C.D.1
10.(2022•河南)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若OE=3,则菱形ABCD的周长为( )
A.6B.12C.24D.48
11.(2022•丽水)如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG∥AD交AE于点G.若csB=,则FG的长是( )
A.3B.C.D.
12.(2022•自贡)如图,菱形ABCD对角线交点与坐标原点O重合,点A(﹣2,5),则点C的坐标是( )
A.(5,﹣2)B.(2,﹣5)C.(2,5)D.(﹣2,﹣5)
13.(2022•泰安)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为( )
A.B.C.﹣D.﹣2
14.(2022•怀化)下列说法正确的是( )
A.相等的角是对顶角
B.对角线相等的四边形是矩形
C.三角形的外心是它的三条角平分线的交点
D.线段垂直平分线上的点到线段两端的距离相等
15.(2022•随州)七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,AP⊥EF分别交BD,EF于O,P两点,M,N分别为BO,DO的中点,连接MP,NF,沿图中实线剪开即可得到一副七巧板.则在剪开之前,关于该图形,下列说法正确的有( )
①图中的三角形都是等腰直角三角形;
②四边形MPEB是菱形;
③四边形PFDM的面积占正方形ABCD面积的.
A.只有①B.①②C.①③D.②③
二.填空题(共14小题)
16.(2022•十堰)“美丽乡村”建设使我市农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF,AG分别架在墙体的点B,C处,且AB=AC,侧面四边形BDEC为矩形.若测得∠FBD=55°,则∠A= °.
17.(2022•邵阳)已知矩形的一边长为6cm,一条对角线的长为10cm,则矩形的面积为 cm2.
18.(2022•宜昌)如图,在矩形ABCD中,E是边AD上一点,F,G分别是BE,CE的中点,连接AF,DG,FG,若AF=3,DG=4,FG=5,矩形ABCD的面积为 .
19.(2022•天津)如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于 .
20.(2022•乐山)已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
21.(2022•武威)如图,菱形ABCD中,对角线AC与BD相交于点O,若AB=2cm,AC=4cm,则BD的长为 cm.
22.(2022•武威)如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是 .
23.(2022•温州)如图,在菱形ABCD中,AB=1,∠BAD=60°.在其内部作形状、大小都相同的菱形AENH和菱形CGMF,使点E,F,G,H分别在边AB,BC,CD,DA上,点M,N在对角线AC上.若AE=3BE,则MN的长为 .
24.(2022•达州)如图,菱形ABCD的对角线AC,BD相交于点O,AC=24,BD=10,则菱形ABCD的周长为 .
25.(2022•丽水)如图,标号为①,②,③,④的矩形不重叠地围成矩形PQMN.已知①和②能够重合,③和④能够重合,这四个矩形的面积都是5.AE=a,DE=b,且a>b.
(1)若a,b是整数,则PQ的长是 ;
(2)若代数式a2﹣2ab﹣b2的值为零,则的值是 .
26.(2022•宿迁)如图,在矩形ABCD中,AB=6,BC=8,点M、N分别是边AD、BC的中点,某一时刻,动点E从点M出发,沿MA方向以每秒2个单位长度的速度向点A匀速运动;同时,动点F从点N出发,沿NC方向以每秒1个单位长度的速度向点C匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接EF,过点B作EF的垂线,垂足为H.在这一运动过程中,点H所经过的路径长是 .
27.(2022•江西)沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 .
28.(2022•达州)如图,在边长为2的正方形ABCD中,点E,F分别为AD,CD边上的动点(不与端点重合),连接BE,BF,分别交对角线AC于点P,Q.点E,F在运动过程中,始终保持∠EBF=45°,连接EF,PF,PD.下列结论:①PB=PD;②∠EFD=2∠FBC;③PQ=PA+CQ;④△BPF为等腰直角三角形;⑤若过点B作BH⊥EF,垂足为H,连接DH,则DH的最小值为2﹣2,其中所有正确结论的序号是 .
29.(2022•安徽)如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:
(1)∠FDG= °;
(2)若DE=1,DF=2,则MN= .
三.解答题(共20小题)
30.(2022•十堰)如图,▱ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF;
(2)设=k,当k为何值时,四边形DEBF是矩形?请说明理由.
31.(2022•随州)如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证:AE=CF;
(2)已知平行四边形ABCD的面积为20,AB=5,求CF的长.
32.(2022•广元)如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积.
33.(2022•山西)如图,在矩形ABCD中,AC是对角线.
(1)实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.
34.(2022•岳阳)如图,点E,F分别在▱ABCD的边AB,BC上,AE=CF,连接DE,DF.请从以下三个条件:①∠1=∠2;②DE=DF;③∠3=∠4中,选择一个合适的作为已知条件,使▱ABCD为菱形.
(1)你添加的条件是 (填序号);
(2)添加了条件后,请证明▱ABCD为菱形.
35.(2022•邵阳)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.
求证:四边形AECF是正方形.
36.(2022•杭州)如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM.
(2)若AB=4,求线段FC的长.
37.(2022•云南)如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,求四边形ABCF的面积S.
38.(2022•舟山)小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
39.(2022•凉山州)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
40.(2022•滨州)如图,菱形ABCD的边长为10,∠ABC=60°,对角线AC、BD相交于点O,点E在对角线BD上,连接AE,作∠AEF=120°且边EF与直线DC相交于点F.
(1)求菱形ABCD的面积;
(2)求证AE=EF.
41.(2022•南充)如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
求证:(1)△ADE≌△CDF.
(2)ME=NF.
42.(2022•德阳)如图,在菱形ABCD中,∠ABC=60°,AB=2cm,过点D作BC的垂线,交BC的延长线于点H.点F从点B出发沿BD方向以2cm/s向点D匀速运动,同时,点E从点H出发沿HD方向以1cm/s向点D匀速运动.设点E,F的运动时间为t(单位:s),且0<t<3,过F作FG⊥BC于点G,连结EF.
(1)求证:四边形EFGH是矩形;
(2)连结FC,EC,点F,E在运动过程中,△BFC与△DCE是否能够全等?若能,求出此时t的值;若不能,请说明理由.
43.(2022•遂宁)如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF∥AC交OE的延长线于点F,连接AF.
(1)求证:△AOE≌△DFE;
(2)判定四边形AODF的形状并说明理由.
44.(2022•苏州)如图,将矩形ABCD沿对角线AC折叠,点B的对应点为点E,AE与CD交于点F.
(1)求证:△DAF≌△ECF;
(2)若∠FCE=40°,求∠CAB的度数.
45.(2022•丽水)如图,将矩形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF;
(2)若CD=4cm,EF=5cm,求BC的长.
46.(2022•自贡)如图,用四根木条钉成矩形框ABCD,把边BC固定在地面上,向右边推动矩形框,矩形的形状会发生改变(四边形具有不稳定性).
(1)通过观察分析,我们发现图中线段存在等量关系,如线段EB由AB旋转得到,所以EB=AB.我们还可以得到FC= ,EF= ;
(2)进一步观察,我们还会发现EF∥AD,请证明这一结论;
(3)已知BC=30cm,DC=80cm,若BE恰好经过原矩形DC边的中点H,求EF与BC之间的距离.
47.(2022•湖州)如图,已知在Rt△ABC中,∠C=Rt∠,D是AB边上一点,以BD为直径的半圆O与边AC相切,切点为E,过点O作OF⊥BC,垂足为F.
(1)求证:OF=EC;
(2)若∠A=30°,BD=2,求AD的长.
48.(2022•湖州)已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.
(1)如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1,正方形BGFC的面积为S2.
①若S1=9,S2=16,求S的值;
②延长EA交GB的延长线于点N,连结FN,交BC于点M,交AB于点H.若FH⊥AB(如图2所示),求证:S2﹣S1=2S.
(2)如图3,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1,等边三角形CBE的面积为S2.以AB为边向上作等边三角形ABF(点C在△ABF内),连结EF,CF.若EF⊥CF,试探索S2﹣S1与S之间的等量关系,并说明理由.
49.(2022•杭州)在正方形ABCD中,点M是边AB的中点,点E在线段AM上(不与点A重合),点F在边BC上,且AE=2BF,连接EF,以EF为边在正方形ABCD内作正方形EFGH.
(1)如图1,若AB=4,当点E与点M重合时,求正方形EFGH的面积.
(2)如图2,已知直线HG分别与边AD,BC交于点I,J,射线EH与射线AD交于点K.
①求证:EK=2EH;
②设∠AEK=α,△FGJ和四边形AEHI的面积分别为S1,S2.求证:=4sin2α﹣1.
小惠:
证明:∵AC⊥BD,OB=OD,
∴AC垂直平分BD.
∴AB=AD,CB=CD,
∴四边形ABCD是菱形.
小洁:
这个题目还缺少条件,需要补充一个条件才能证明.
备战2023年中考数学必刷真题考点分类专练(全国通用)
专题18矩形菱形正方形(共49题)
一.选择题(共15小题)
1.(2022•陕西)在下列条件中,能够判定▱ABCD为矩形的是( )
A.AB=ADB.AC⊥BDC.AB=ACD.AC=BD
【分析】由矩形的判定和菱形的判定分别对各个选项进行判断即可.
【解析】A.∵▱ABCD中,AB=AD,
∴▱ABCD是菱形,故选项A不符合题意;
B.∵▱ABCD中,AC⊥BD,
∴▱ABCD是菱形,故选项B不符合题意;
C.▱ABCD中,AB=AC,不能判定▱ABCD是矩形,故选项C不符合题意;
D.∵▱ABCD中,AC=BD,
∴▱ABCD是矩形,故选项D符合题意;
故选:D.
2.(2022•株洲)如图所示,在菱形ABCD中,对角线AC与BD相交于点O,过点C作CE∥BD交AB的延长线于点E,下列结论不一定正确的是( )
A.OB=CEB.△ACE是直角三角形
C.BC=AED.BE=CE
【分析】由菱形的性质可得AO=CO=,AC⊥BD,通过证明△AOB∽△ACE,可得∠AOB=∠ACE=90°,OB=CE,AB=AE,由直角三角形的性质可得BC=AE,即可求解.
【解析】∵四边形ABCD是菱形,
∴AO=CO=,AC⊥BD,
∵CE∥BD,
∴△AOB∽△ACE,
∴∠AOB=∠ACE=90°,=,
∴△ACE是直角三角形,OB=CE,AB=AE,
∴BC=AE,
故选:D.
3.(2022•宁波)将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
A.正方形纸片的面积B.四边形EFGH的面积
C.△BEF的面积D.△AEH的面积
【分析】根据题意设PD=x,GH=y,则PH=x﹣y,根据矩形纸片和正方形纸片的周长相等,可得AP=x+y,先用面积差表示图中阴影部分的面积,并化简,再用字母分别表示出图形四个选项的面积,可得出正确的选项.
【解析】设PD=x,GH=y,则PH=x﹣y,
∵矩形纸片和正方形纸片的周长相等,
∴2AP+2(x﹣y)=4x,
∴AP=x+y,
∵图中阴影部分的面积=S矩形ABCD﹣2△ADH﹣2S△AEB
=(2x+y)(2x﹣y)﹣2ו(x﹣y)(2x+y)﹣2ו(2x﹣y)•x
=4x2﹣y2﹣(2x2+xy﹣2xy﹣y2)﹣(2x2﹣xy)
=4x2﹣y2﹣2x2+xy+y2﹣2x2+xy
=2xy,
A、正方形纸片的面积=x2,故A不符合题意;
B、四边形EFGH的面积=y2,故B不符合题意;
C、△BEF的面积=•EF•BQ=xy,故C符合题意;
D、△AEH的面积=•EH•AM=y(x﹣y)=xy﹣y2,故D不符合题意;
故选:C.
4.(2022•安徽)两个矩形的位置如图所示,若∠1=α,则∠2=( )
A.α﹣90°B.α﹣45°C.180°﹣αD.270°﹣α
【分析】根据矩形的性质和三角形外角的性质,可以用含α的式子表示出∠2.
【解析】由图可得,
∠1=90°+∠3,
∵∠1=α,
∴∠3=α﹣90°,
∵∠3+∠2=90°,
∴∠2=90°﹣∠3=90°﹣(α﹣90°)=90°﹣α+90°=180°﹣α,
故选:C.
5.(2022•滨州)下列命题,其中是真命题的是( )
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
【分析】根据,平行四边形,矩形,菱形,正方形的判定方法一一判断即可.
【解析】A、对角线互相垂直的四边形是平行四边形,是假命题,本选项不符合题意;
B、有一个角是直角的四边形是矩形,是假命题,本选项不符合题意;
C、对角线互相平分的四边形是菱形,是假命题,本选项不符合题意;
D、对角线互相垂直的矩形是正方形,是真命题,本选项符合题意.
故选:D.
6.(2022•绍兴)如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,边BC上的动点.下列四种说法:
①存在无数个平行四边形MENF;
②存在无数个矩形MENF;
③存在无数个菱形MENF;
④存在无数个正方形MENF.
其中正确的个数是( )
A.1B.2C.3D.4
【分析】根据题意作出合适的辅助线,然后逐一分析即可.
【解析】连接AC,MN,且令AC,MN,BD相交于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
只要OM=ON,那么四边形MENF就是平行四边形,
∵点E,F是BD上的动点,
∴存在无数个平行四边形MENF,故①正确;
只要MN=EF,OM=ON,则四边形MENF是矩形,
∵点E,F是BD上的动点,
∴存在无数个矩形MENF,故②正确;
只要MN⊥EF,OM=ON,则四边形MENF是菱形,
∵点E,F是BD上的动点,
∴存在无数个菱形MENF,故③正确;
只要MN=EF,MN⊥EF,OM=ON,则四边形MENF是正方形,
而符合要求的正方形只有一个,故④错误;
故选:C.
7.(2022•重庆)如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若BE=AF,则∠CDF的度数为( )
A.45°B.60°C.67.5°D.77.5°
【分析】根据正方形的性质和全等三角形的判定和性质,可以得到∠ADF的度数,从而可以求得∠CDF的度数.
【解析】∵四边形ABCD是正方形,
∴AD=BA,∠DAF=∠ABE=90°,
在△DAF和△ABE中,
,
△DAF≌△ABE(SAS),
∠ADF=∠BAE,
∵AE平分∠BAC,四边形ABCD是正方形,
∴∠BAE=∠BAC=22.5°,∠ADC=90°,
∴∠ADF=22.5°,
∴∠CDF=∠ADC﹣∠ADF=90°﹣22.5°=67.5°,
故选:C.
8.(2022•重庆)如图,在正方形ABCD中,对角线AC、BD相交于点O.E、F分别为AC、BD上一点,且OE=OF,连接AF,BE,EF.若∠AFE=25°,则∠CBE的度数为( )
A.50°B.55°C.65°D.70°
【分析】利用正方形的对角线互相垂直平分且相等,等腰直角三角形的性质,三角形的内角和定理和全等三角形的判定与性质解答即可.
【解析】∵ABCD是正方形,
∴∠AOB=∠AOD=90°,OA=OB=OD=OC.
∵OE=OF,
∴△OEF为等腰直角三角形,
∴∠OEF=∠OFE=45°,
∵∠AFE=25°,
∴∠AFO=∠AFE+∠OFE=70°,
∴∠FAO=20°.
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS).
∴∠FAO=∠EOB=20°,
∵OB=OC,
∴△OBC是等腰直角三角形,
∴∠OBC=∠OCB=45°,
∴∠CBE=∠EBO+∠OBC=65°.
故选:C.
9.(2022•泸州)如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为( )
A.B.C.D.1
【分析】根据正方形的性质、相似三角形的判定和性质,可以求得CN和BN的长,然后根据BC=3,即可求得MN的长.
【解析】作FH⊥BG交于点H,作FK⊥BC于点K,
∵BF平分∠CBG,∠KBH=90°,
∴正方形BHFK是正方形,
∵DE⊥EF,∠EHF=90°,
∴∠DEA+∠FEH=90°,∠EFH+∠FEH=90°,
∴∠DEA=∠EFH,
∵∠A=∠EHF=90°,
∴△DAE∽△EHF,
∴,
∵正方形ABCD的边长为3,BE=2AE,
∴AE=1,BE=2,
设FH=a,则BH=a,
∴,
解得a=1;
∵FM⊥CB,DC⊥CB,
∴△DCN∽△FKN,
∴,
∵BC=3,BK=1,
∴CK=2,
设CN=b,则NK=2﹣b,
∴,
解得b=,
即CN=,
∵∠A=∠EBM,∠AED=∠BME,
∴△ADE∽△BEM,
∴,
∴,
解得BM=,
∴MN=BC﹣CN﹣BM=3﹣﹣=,
故选:B.
10.(2022•河南)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若OE=3,则菱形ABCD的周长为( )
A.6B.12C.24D.48
【分析】由菱形的性质可得出AC⊥BD,AB=BC=CD=DA,再根据直角三角形斜边上的中线等于斜边的一半得出CD的长,结合菱形的周长公式即可得出结论.
【解析】∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△COD为直角三角形.
∵OE=3,点E为线段CD的中点,
∴CD=2OE=6.
∴C菱形ABCD=4CD=4×6=24.
故选:C.
11.(2022•丽水)如图,已知菱形ABCD的边长为4,E是BC的中点,AF平分∠EAD交CD于点F,FG∥AD交AE于点G.若csB=,则FG的长是( )
A.3B.C.D.
【分析】方法一:过点A作AH⊥BE于点H,过点F作FQ⊥AD于点Q,根据csB==,可得BH=1,所以AH=,然后证明AH是BE的垂直平分线,可得AE=AB=4,设GA=GF=x,根据S梯形CEAD=S梯形CEGF+S梯形GFAD,进而可以解决问题.方法二:作AH垂直BC于H,延长AE和DC交于点M由已知可得BH=EH=1,所以AE=AB=EM=CM=4设GF=x,则AG=x,GE=4﹣x,由三角形MGF相似于三角形MEC即可得结论.
【解析】方法一,如图,过点A作AH⊥BE于点H,过点F作FQ⊥AD于点Q,
∵菱形ABCD的边长为4,
∴AB=AD=BC=4,
∵csB==,
∴BH=1,
∴AH===,
∵E是BC的中点,
∴BE=CE=2,
∴EH=BE﹣BH=1,
∴AH是BE的垂直平分线,
∴AE=AB=4,
∵AF平分∠EAD,
∴∠DAF=∠FAG,
∵FG∥AD,
∴∠DAF=∠AFG,
∴∠FAG=∠AFG,
∴GA=GF,
设GA=GF=x,
∵AE=CD,FG∥AD,
∴DF=AG=x,
csD=csB==,
∴DQ=x,
∴FQ===x,
∵S梯形CEAD=S梯形CEGF+S梯形GFAD,
∴×(2+4)×=(2+x)×(﹣x)+(x+4)×x,
解得x=,
则FG的长是.
方法二:如图,作AH垂直BC于H,延长AE和DC交于点M,
由已知可得BH=EH=1,
所以AE=AB=EM=CM=4,
设GF=x,
则AG=x,GE=4﹣x,
由GF∥BC,
∴△MGF∽△MEC,
∴=,
解得x=.
故选:B.
12.(2022•自贡)如图,菱形ABCD对角线交点与坐标原点O重合,点A(﹣2,5),则点C的坐标是( )
A.(5,﹣2)B.(2,﹣5)C.(2,5)D.(﹣2,﹣5)
【分析】菱形的对角线相互平分可知点A与C关于原点对称,从而得结论.
【解析】∵四边形ABCD是菱形,
∴OA=OC,即点A与点C关于原点对称,
∵点A(﹣2,5),
∴点C的坐标是(2,﹣5).
故选:B.
13.(2022•泰安)如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为( )
A.B.C.﹣D.﹣2
【分析】如图,取AD的中点O,连接OB,OM.证明∠AMD=90°,推出OM=AD=2,点M的运动轨迹是以O为圆心,2为半径的⊙O.利用勾股定理求出OB,可得结论.
【解析】如图,取AD的中点O,连接OB,OM.
∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=4,
∴∠BAP+∠DAM=90°,
∵∠ADM=∠BAP,
∴∠ADM+∠DAM=90°,
∴∠AMD=90°,
∵AO=OD=2,
∴OM=AD=2,
∴点M的运动轨迹是以O为圆心,2为半径的⊙O.
∵OB===,
∴BM≥OB﹣OM=﹣2,
∴BM的最小值为﹣2.
故选:D.
14.(2022•怀化)下列说法正确的是( )
A.相等的角是对顶角
B.对角线相等的四边形是矩形
C.三角形的外心是它的三条角平分线的交点
D.线段垂直平分线上的点到线段两端的距离相等
【分析】根据对顶角的定义,矩形的判定,三角形的外心,线段垂直平分线的性质可得出答案.
【解析】A、相等的角不一定是对顶角,故本选项说法错误,不符合题意;
B、对角线相等的四边形不一定是矩形,故本选项说法错误,不符合题意;
C、三角形的外心是它的三条边的垂直平分线的交点,故本选项说法错误,不符合题意;
D、线段垂直平分线上的点到线段两端的距离相等,故本选项符合题意.
故选:D.
15.(2022•随州)七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,AP⊥EF分别交BD,EF于O,P两点,M,N分别为BO,DO的中点,连接MP,NF,沿图中实线剪开即可得到一副七巧板.则在剪开之前,关于该图形,下列说法正确的有( )
①图中的三角形都是等腰直角三角形;
②四边形MPEB是菱形;
③四边形PFDM的面积占正方形ABCD面积的.
A.只有①B.①②C.①③D.②③
【分析】①利用正方形的性质和中位线的性质可以解决问题;
②利用①的结论可以证明OM≠MP解决问题;
③如图,过M作MG⊥BC于G,设AB=BC=x,利用正方形的性质与中位线的性质分别求出BE和MG即可判定是否正确.
【解析】①如图,∵E,F分别为BC,CD的中点,
∴EF为△CBD的中位线,
∴EF∥BD,
∵AP⊥EF,
∴AP⊥BD,
∵四边形ABCD为正方形,
∴A、O、P、C在同一条直线上,
∴△ABC、△ACD、△ABD、△BCD、△OAB、△OAD、△OBC、△OCD、△EFC都是等腰直角三角形,
∵M,N分别为BO,DO的中点,
∴MP∥BC,NF∥OC,
∴△DNF、△OMP也是等腰直角三角形.
故①正确;
②根据①得OM=BM=PM,∴BM≠PM
∴四边形MPEB不可能是菱形.故②错误;
③∵E,F分别为BC,CD的中点,
∴EF∥BD,EF=BD,
∵四边形ABCD是正方形,且设AB=BC=x,
∴BD=x,
∵AP⊥EF,
∴AP⊥BD,
∴BO=OD,
∴点P在AC上,
∴PE=EF,
∴PE=BM,
∴四边形BMPE是平行四边形,
∴BO=BD,
∵M为BO的中点,
∴BM=BD=x,
∵E为BC的中点,
∴BE=BC=x,
过M作MG⊥BC于G,
∴MG=BM=x,
∴四边形BMPE的面积=BE•MG=x2,
∴四边形PFDM的面积占正方形ABCD面积的.
∵E、F是BC,CD的中点,
∴S△CEF=S△CBD=S四边形ABCD,
∴四边形PFDM的面积占正方形ABCD面积的(1﹣﹣)=.
故③正确.
故选:C.
二.填空题(共14小题)
16.(2022•十堰)“美丽乡村”建设使我市农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF,AG分别架在墙体的点B,C处,且AB=AC,侧面四边形BDEC为矩形.若测得∠FBD=55°,则∠A= 110 °.
【分析】利用矩形的性质可得∠DBC=90°,从而利用平角定义求出∠ABC的度数,然后利用等腰三角形的性质可得∠ABC=∠ACB=35°,最后利用三角形内角和定理进行计算即可解答.
【解析】∵四边形BDEC为矩形,
∴∠DBC=90°,
∵∠FBD=55°,
∴∠ABC=180°﹣∠DBC﹣∠FBD=35°,
∵AB=AC,
∴∠ABC=∠ACB=35°,
∴∠A=180°﹣∠ABC﹣∠ACB=110°,
故答案为:110.
17.(2022•邵阳)已知矩形的一边长为6cm,一条对角线的长为10cm,则矩形的面积为 48 cm2.
【分析】利用勾股定理列式求出另一边长,然后根据矩形的面积公式列式进行计算即可得解.
【解析】∵长方形的一条对角线的长为10cm,一边长为6cm,
∴另一边长==8cm,
∴它的面积为8×6=48cm2.
故答案为:48.
18.(2022•宜昌)如图,在矩形ABCD中,E是边AD上一点,F,G分别是BE,CE的中点,连接AF,DG,FG,若AF=3,DG=4,FG=5,矩形ABCD的面积为 48 .
【分析】由矩形的性质得出∠BAE=∠CDE=90°,AD∥BC,由直角三角形斜边上中线的性质及三角形中位线的性质求出BE=6,CE=8,BC=10,由勾股定理的逆定理得出△BCE是直角三角形,∠BEC=90°,进而求出=24,即可求出矩形ABCD的面积.
【解析】∵四边形ABCD是矩形,
∴∠BAE=∠CDE=90°,AD∥BC,
∵F,G分别是BE,CE的中点,AF=3,DG=4,FG=5,
∴BE=2AF=6,CE=2DG=8,BC=2FG=10,
∴BE2+CE2=BC2,
∴△BCE是直角三角形,∠BEC=90°,
∴==24,
∵AD∥BC,
∴S矩形ABCD=2S△BCE=2×24=48,
故答案为:48.
19.(2022•天津)如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于 .
【分析】如图,过点F作FH∥CD,交DE于H,过点C作CM⊥AB,交AB的延长线于M,连接FB,先证明FH是△CDE的中位线,得FH=1,再证明△AEG≌△FHG(AAS),得AG=FG,在Rt△CBM中计算BM和CM的长,再证明BF是中位线,可得BF的长,由勾股定理可得AF的长,从而得结论.
【解析】如图,过点F作FH∥CD,交DE于H,过点C作CM⊥AB,交AB的延长线于M,连接FB,
∵四边形ABCD是菱形,
∴AB=CD=BC=2,AB∥CD,
∴FH∥AB,
∴∠FHG=∠AEG,
∵F是CE的中点,FH∥CD,
∴H是DE的中点,
∴FH是△CDE的中位线,
∴FH=CD=1,
∵E是AB的中点,
∴AE=BE=1,
∴AE=FH,
∵∠AGE=∠FGH,
∴△AEG≌△FHG(AAS),
∴AG=FG,
∵AD∥BC,
∴∠CBM=∠DAB=60°,
Rt△CBM中,∠BCM=30°,
∴BM=BC=1,CM==,
∴BE=BM,
∵F是CE的中点,
∴FB是△CEM的中位线,
∴BF=CM=,FB∥CM,
∴∠EBF=∠M=90°,
Rt△AFB中,由勾股定理得:AF===,
∴GF=AF=.
故答案为:.
20.(2022•乐山)已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 24 cm2.
【分析】根据菱形的面积=对角线乘积的一半,可以计算出该菱形的面积.
【解析】∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm,
∴菱形的面积是=24(cm2),
故答案为:24.
21.(2022•武威)如图,菱形ABCD中,对角线AC与BD相交于点O,若AB=2cm,AC=4cm,则BD的长为 8 cm.
【分析】由菱形的性质可得AC⊥BD,BO=DO,由勾股定理可求BO,即可求解.
【解析】∵四边形ABCD是菱形,AC=4cm,
∴AC⊥BD,BO=DO,AO=CO=2cm,
∵AB=2cm,
∵BO==4cm,
∴DO=BO=4cm,
∴BD=8cm,
故答案为:8.
22.(2022•武威)如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是 ∠A=90°(答案不唯一) .
【分析】先证四边形ABCD是平行四边形,再由矩形的判定即可得出结论.
【解析】需添加的一个条件是∠A=90°,理由如下:
∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴平行四边形ABCD是矩形,
故答案为:∠A=90°(答案不唯一).
23.(2022•温州)如图,在菱形ABCD中,AB=1,∠BAD=60°.在其内部作形状、大小都相同的菱形AENH和菱形CGMF,使点E,F,G,H分别在边AB,BC,CD,DA上,点M,N在对角线AC上.若AE=3BE,则MN的长为 .
【分析】方法一:根据菱形的性质和锐角三角函数,可以求得AC、AM和MN的长,然后即可计算出MN的长.
方法二:根据相似三角形的判定和性质可以得到EF和MN的关系,然后解直角三角形可以求得OA的长,从而可以得到MN的长.
【解析】方法一:连接DB交AC于点O,作MI⊥AB于点I,作FJ⊥AB交AB的延长线于点J,如图1所示,
∵四边形ABCD是菱形,∠BAD=60°,AB=1,
∴AB=BC=CD=DA=1,∠BAC=30°,AC⊥BD,
∵△ABD是等边三角形,
∴OD=,
∴AO===,
∴AC=2AO=,
∵AE=3BE,
∴AE=,BE=,
∵菱形AENH和菱形CGMF大小相同,
∴BE=BF=,∠FBJ=60°,
∴FJ=BF•sin60°=×=,
∴MI=FJ=,
∴AM===,
同理可得,CN=,
∴MN=AC﹣AM﹣CN=﹣=,
故答案为:.
方法二:连接DB交AC于点O,连接EF,
由题意可得,四边形AMFE是平行四边形,四边形EFCN是平行四边形,
∴EF=AM=CN,
∵EF∥AC,
∴△BEF∽△BAC,
∴,
∵AE=3BE,AB=1,
∴AB=4BE,
∴=,
∴AM=CN=AC,
∴MN=AC=OA,
∵∠BAD=60°.AB=AD=1,AO垂直平分BD,
∴OD=,
∴OA===,
∴MN=,
故答案为:.
24.(2022•达州)如图,菱形ABCD的对角线AC,BD相交于点O,AC=24,BD=10,则菱形ABCD的周长为 52 .
【分析】菱形的四条边相等,要求周长,只需求出边长即可,菱形的对角线互相垂直且平分,根据勾股定理求边长即可.
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BD,AO=CO,BO=DO,
∵AC=24,BD=10,
∴AO=AC=12,BO=BD=5,
在Rt△AOB中,
AB===13,
∴菱形的周长=13×4=52.
故答案为:52.
25.(2022•丽水)如图,标号为①,②,③,④的矩形不重叠地围成矩形PQMN.已知①和②能够重合,③和④能够重合,这四个矩形的面积都是5.AE=a,DE=b,且a>b.
(1)若a,b是整数,则PQ的长是 任意正整数 ;
(2)若代数式a2﹣2ab﹣b2的值为零,则的值是 3+2 .
【分析】(1)直接根据线段的差可得结论;
(2)先把b当常数解方程:a2﹣2ab﹣b2=0,a=b+b(负值舍),根据四个矩形的面积都是5表示小矩形的宽,最后计算面积的比,化简后整体代入即可解答.
【解析】(1)由图可知:PQ=a﹣b,
∵a,b是整数,a>b,
∴PQ的长是任意正整数;
故答案为:任意正整数;
(2)∵a2﹣2ab﹣b2=0,
∴a2﹣b2=2ab,(a﹣b)2=2b2,
∴a=b+b(负值舍),
∵四个矩形的面积都是5.AE=a,DE=b,
∴EP=,EN=,
则======3+2.
故答案为:3+2.
26.(2022•宿迁)如图,在矩形ABCD中,AB=6,BC=8,点M、N分别是边AD、BC的中点,某一时刻,动点E从点M出发,沿MA方向以每秒2个单位长度的速度向点A匀速运动;同时,动点F从点N出发,沿NC方向以每秒1个单位长度的速度向点C匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接EF,过点B作EF的垂线,垂足为H.在这一运动过程中,点H所经过的路径长是 π .
【分析】如图1中,连接MN交EF于点P,连接BP.首先证明PN=2,利用勾股定理求出BP.由∠BPH=90°,推出点H在BP为直径的⊙O上运动,当点E与A重合时,如图2中,连接OH,ON.点H的运动轨迹是.求出∠HON,再利用弧长公式求解.
【解析】如图1中,连接MN交EF于点P,连接BP.
∵四边形ABCD是矩形,AM=MD,BN=CN,
∴四边形ABNM是矩形,
∴MN=AB=6,
∵EM∥NF,
∴△EPM∽△FPN,
∴===2,
∴PN=2,PM=4,
∵BN=4,
∴BP===2,
∵BH⊥EF,
∴∠BPH=90°,
∴点H在BP为直径的⊙O上运动,
当点E与A重合时,如图2中,连接OH,ON.点H的运动轨迹是.
此时AM=4,NF=2,
∴BF=AB=6,
∵∠ABF=90°,BH⊥AF,
∴BH平分∠ABF,
∴∠HBN=45°,
∴∠HON=2∠HBN=90°,
∴点H的运动轨迹的长==π.
故答案为:π.
27.(2022•江西)沐沐用七巧板拼了一个对角线长为2的正方形,再用这副七巧板拼成一个长方形(如图所示),则长方形的对角线长为 .
【分析】根据图形可得长方形的长是正方形的对角线为2,长方形的宽是正方形对角线的一半为1,然后利用勾股定理即可解决问题.
【解析】根据图形可知:长方形的长是正方形的对角线为2,
长方形的宽是正方形对角线的一半为1,
则长方形的对角线长==.
故答案为:.
28.(2022•达州)如图,在边长为2的正方形ABCD中,点E,F分别为AD,CD边上的动点(不与端点重合),连接BE,BF,分别交对角线AC于点P,Q.点E,F在运动过程中,始终保持∠EBF=45°,连接EF,PF,PD.下列结论:①PB=PD;②∠EFD=2∠FBC;③PQ=PA+CQ;④△BPF为等腰直角三角形;⑤若过点B作BH⊥EF,垂足为H,连接DH,则DH的最小值为2﹣2,其中所有正确结论的序号是 ①②④⑤ .
【分析】①正确.证明△BCP≌△DCP(SAS),可得结论;
②正确.证明∠CFB=∠EFB,推出∠CBF+∠CFB=90°,推出2∠CBF+2∠CFB=180°,由∠EFD+2∠CFB=180°,可得结论;
③错误.可以证明PQ<PA+CQ;
④正确.利用相似三角形的性质证明∠BPF=90°,可得结论;
⑤正确.求出BD,BH,根据DH≥BD﹣BH,可得结论.
【解析】如图,∵四边形ABCD是正方形,
∴CB=CD,∠BCP=∠DCP=45°,
在△BCP和△DCP中,
,
∴△BCP≌△DCP(SAS),
∴PB=PD,故①正确,
∵∠PBQ=∠QCF=45°,∠PQB=∠FQC,
∴△PQB∽△FQC,
∴=,∠BPQ=∠CFQ,
∴=,
∵∠PQF=∠BQC,
∴△PQF∽△BQC,
∴∠QPF=∠QBC,
∵∠QBC+∠CFQ=90°,
∴∠BPF=∠BPQ+∠QPF=90°,
∴∠PBF=∠PFB=45°,
∴PB=PF,
∴△BPF是等腰直角三角形,故④正确,
∵∠EPF=∠EDF=90°,
∴E,D,F,P四点共圆,
∴∠PEF=∠PDF,
∵PB=PD=PF,
∴∠PDF=∠PFD,
∵∠AEB+∠DEP=180°,∠DEP+∠DFP=180°,
∴∠AEB=∠DFP,
∴∠AEB=∠BEH,
∵BH⊥EF,
∴∠BAE=∠BHE=90°,
∵BE=BE,
∴△BEA≌△BEH(AAS),
∴AB=BH=CF=BC,
∵∠BHF=∠BCF=90°,BF=BF,
∴Rt△BFH≌Rt△BFC(HL),
∴∠BFC=∠BFH,
∵∠CBF+∠BFC=90°,
∴2∠CBF+2∠CFB=180°,
∵∠EFD+∠CFH=∠EFD+2∠CFB=180°,
∴∠EFD=2∠CBFM故②正确,
将△ABP绕点B顺时针旋转90°得到△BCT,连接QT,
∴∠ABP=∠CBT,
∴∠PBT=∠ABC=90°,
∴∠PBQ=∠TBQ=45°,
∵BQ=BQ,BP=BT,
∴△BQP≌△BQT(SAS),
∴PQ=QT,
∵QT<CQ+CT=CQ+AP,
∴PQ<AP+CQ,故③错误,
连接BD,DH,
∵BD=2,BH=AB=2,
∴DH≥BD﹣BH=2﹣2,
∴DH的最小值为2﹣2,故⑤正确,
故答案为:①②④⑤.
29.(2022•安徽)如图,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,请完成下列问题:
(1)∠FDG= 45 °;
(2)若DE=1,DF=2,则MN= .
【分析】(1)根据AAS证△ABE≌△GEF,得出EG=AB,GF=AE,推出DG=GF即可得出∠FDG的度数;
(2)由(1)的结论得出CD的长度,GF的长度,根据相似三角形的性质分别求出DM,NC的值即可得出MN的值.
【解析】由题知,△BEF是以E为直角顶点的等腰直角三角形,
∴∠AEB+∠GEF=90°,
∵∠AEB+∠ABE=90°,
∴∠GEF=∠ABE,
在△ABE和△GEF中,
,
∴△ABE≌△GEF(AAS),
∴EG=AB=AD,GF=AE,
即DG+DE=AE+DE,
∴DG=AE,
∴DG=GF,
即△DGF是等腰直角三角形,
∴∠FDG=45°,
故答案为:45°;
(2)∵DE=1,DF=2,
由(1)知,△DGF是等腰直角三角形,
∴DG=GF=2,AB=AD=CD=ED+DG=2+1=3,
延长GF交BC延长线于点H,
∴CD∥GH,
∴△EDM∽△EGF,
∴,
即,
∴MD=,
同理△BNC∽△BFH,
∴,
即,
∴,
∴NC=,
∴MN=CD﹣MD﹣NC=3﹣﹣=,
故答案为:.
三.解答题(共20小题)
30.(2022•十堰)如图,▱ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF;
(2)设=k,当k为何值时,四边形DEBF是矩形?请说明理由.
【分析】(1)利用平行四边形的性质,即可得到BO=OD,EO=FO,进而得出四边形BFDE是平行四边形,进而得到DE=BF;
(2)先确定当OE=OD时,四边形DEBF是矩形,从而得k的值.
【解答】(1)证明:如图,连接DE,BF,
∵四边形ABCD是平行四边形,
∴BO=OD,AO=OC,
∵E,F分别为AO,OC的中点,
∴EO=OA,OF=OC,
∴EO=FO,
∵BO=OD,EO=FO,
∴四边形BFDE是平行四边形,
∴DE=BF;
(2)解:当k=2时,四边形DEBF是矩形;理由如下:
当BD=EF时,四边形DEBF是矩形,
∴当OD=OE时,四边形DEBF是矩形,
∵AE=OE,
∴当k=2时,四边形DEBF是矩形.
故答案为:2.
31.(2022•随州)如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证:AE=CF;
(2)已知平行四边形ABCD的面积为20,AB=5,求CF的长.
【分析】(1)根据正方形的性质可以得到DF=EB,根据平行四边形的性质可以得到AB=CD,然后即可得到结论成立;
(2)根据平行四边形的面积,可以得到DE的长,然后根据正方形的性质,可以得到BE的长,从而可以求得AE的长,再根据(1)中的结论,即可得到CF的长.
【解答】(1)证明:∵四边形BEDF为正方形,
∴DF=EB,
∵四边形ABCD是平行四边形,
∴DC=AB,
∴DC﹣DF=AB﹣EB,
∴CF=AE,
即AE=CF;
(2)解:∵平行四边形ABCD的面积为20,AB=5,四边形BEDF为正方形,
∴5DE=20,DE=EB,
∴DE=EB=4,
∴AE=AB﹣EB=5﹣4=1,
由(1)知:AE=CF,
∴CF=1.
32.(2022•广元)如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.
(1)求证:四边形AECD为菱形;
(2)若∠D=120°,DC=2,求△ABC的面积.
【分析】(1)由一组对边平行且相等的四边形是平行四边形,可证四边形AECD是平行四边形,由平行线的性质和角平分线的性质可证AD=CD,可得结论;
(2)由菱形的性质可求AE=BE=CE=2,由等边三角形的性质和直角三角形的性质可求BC,AC的长,即可求解.
【解答】(1)证明:∵E为AB中点,
∴AB=2AE=2BE,
∵AB=2CD,
∴CD=AE,
又∵AE∥CD,
∴四边形AECD是平行四边形,
∵AC平分∠DAB,
∴∠DAC=∠EAC,
∵AB∥CD,
∴∠DCA=∠CAB,
∴∠DCA=∠DAC,
∴AD=CD,
∴平行四边形AECD是菱形;
(2)∵四边形AECD是菱形,∠D=120°,
∴AD=CD=CE=AE=2,∠D=120°=∠AEC,
∴AE=CE=BE,∠CEB=60°,
∴∠CAE=30°=∠ACE,△CEB是等边三角形,
∴BE=BC=EC=2,∠B=60°,
∴∠ACB=90°,
∴AC=BC=2,
∴S△ABC=×AC×BC=×2×2=2.
33.(2022•山西)如图,在矩形ABCD中,AC是对角线.
(1)实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.
【分析】(1)利用尺规作图﹣线段垂直平分线的作法,进行作图即可;
(2)利用矩形的性质求证∠EAO=∠FCO,∠AEO=∠CFO,由线段的垂直平分线得出AO=CO,即可证明△AOE≌△COF,进而得出AE=CF.
【解析】(1)如图,
(2)AE=CF,证明如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∵EF是AC的垂直平分线,
∴AO=CO,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=CF.
34.(2022•岳阳)如图,点E,F分别在▱ABCD的边AB,BC上,AE=CF,连接DE,DF.请从以下三个条件:①∠1=∠2;②DE=DF;③∠3=∠4中,选择一个合适的作为已知条件,使▱ABCD为菱形.
(1)你添加的条件是 ①或③ (填序号);
(2)添加了条件后,请证明▱ABCD为菱形.
【分析】(1)添加合适的条件即可;
(2)添加①,证△ADE≌△CDF(AAS),得AD=CD,再由菱形的判定即可得出结论;添加③,证△ADE≌△CDF(ASA),得AD=CD,再由菱形的判定即可得出结论.
【解答】(1)解:添加的条件是∠1=∠2或∠3=∠4,
故答案为:①或③;
(2)证明:添加①,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AD=CD,
∴▱ABCD为菱形;
添加③,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AD=CD,
∴▱ABCD为菱形.
35.(2022•邵阳)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.
求证:四边形AECF是正方形.
【分析】证明AC与EF互相垂直平分便可根据菱形的判定定理得出结论
【解答】证明:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
∴四边形AECF是菱形;
∴OE=OF,OA=OC,
∵OE=OA=OF,
∴OE=OF=OA=OC,即EF=AC,
∴菱形AECF是正方形.
36.(2022•杭州)如图,在Rt△ACB中,∠ACB=90°,点M为边AB的中点,点E在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.
(1)求证:CE=CM.
(2)若AB=4,求线段FC的长.
【分析】(1)根据直角三角形的性质可得MC=MA=MB,根据外角的性质可得∠MEC=∠A+∠ACE,∠EMC=∠B+∠MCB,根据等角对等边即可得证;
(2)根据CE=CM先求出CE的长,再解直角三角形即可求出FC的长.
【解答】(1)证明:∵∠ACB=90°,点M为边AB的中点,
∴MC=MA=MB,
∴∠MCA=∠A,∠MCB=∠B,
∵∠A=50°,
∴∠MCA=50°,∠MCB=∠B=40°,
∴∠EMC=∠MCB+∠B=80°,
∵∠ACE=30°,
∴∠MEC=∠A+∠ACE=80°,
∴∠MEC=∠EMC,
∴CE=CM;
(2)解:∵AB=4,
∴CE=CM=AB=2,
∵EF⊥AC,∠ACE=30°,
∴FC=CE•cs30°=.
37.(2022•云南)如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,∠BDF=90°.
(1)求证:四边形ABDF是矩形;
(2)若AD=5,DF=3,求四边形ABCF的面积S.
【分析】(1)由四边形ABCD是平行四边形,得∠BAE=∠FDE,而点E是AD的中点,可得△BEA≌△FED(ASA),即知EF=EB,从而四边形ABDF是平行四边形,又∠BDF=90°,即得四边形ABDF是矩形;
(2)由∠AFD=90°,AB=DF=3,AF=BD,得AF===4,S矩形ABDF=DF•AF=12,四边形ABCD是平行四边形,得CD=AB=3,从而S△BCD=BD•CD=6,即可得四边形ABCF的面积S为18.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴BA∥CD,
∴∠BAE=∠FDE,
∵点E是AD的中点,
∴AE=DE,
在△BEA和△FED中,
,
∴△BEA≌△FED(ASA),
∴EF=EB,
又∵AE=DE,
∴四边形ABDF是平行四边形,
∵∠BDF=90°.
∴四边形ABDF是矩形;
(2)解:由(1)得四边形ABDF是矩形,
∴∠AFD=90°,AB=DF=3,AF=BD,
∴AF===4,
∴S矩形ABDF=DF•AF=3×4=12,BD=AF=4,
∵四边形ABCD是平行四边形,
∴CD=AB=3,
∴S△BCD=BD•CD=×4×3=6,
∴四边形ABCF的面积S=S矩形ABDF+S△BCD=12+6=18,
答:四边形ABCF的面积S为18.
38.(2022•舟山)小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.
【分析】根据“对角线互相垂直的平行四边形是菱形”进行分析推理.
【解析】赞成小洁的说法,补充条件:OA=OC,证明如下:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形.
39.(2022•凉山州)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.
(1)求证:四边形ADBF是菱形;
(2)若AB=8,菱形ADBF的面积为40.求AC的长.
【分析】(1)利用平行线的性质可得∠AFC=∠FCD,∠FAE=∠CDE,利用中点的定义可得AE=DE,从而证明△FAE≌△CDE,然后利用全等三角形的性质可得AF=CD,再根据D是BC的中点,可得AF=BD,从而可证四边形AFBD是平行四边形,最后利用直角三角形斜边上的中线可得BD=AD,从而利用菱形的判定定理即可解答;
(2)利用(1)的结论可得菱形ADBF的面积=2△ABD的面积,再根据点D是BC的中点,可得△ABC的面积=2△ABD的面积,进而可得菱形ADBF的面积=△ABC的面积,然后利用三角形的面积进行计算即可解答.
【解答】(1)证明:∵AF∥BC,
∴∠AFC=∠FCD,∠FAE=∠CDE,
∵点E是AD的中点,
∴AE=DE,
∴△FAE≌△CDE(AAS),
∴AF=CD,
∵点D是BC的中点,
∴BD=CD,
∴AF=BD,
∴四边形AFBD是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BD=BC,
∴四边形ADBF是菱形;
(2)解:∵四边形ADBF是菱形,
∴菱形ADBF的面积=2△ABD的面积,
∵点D是BC的中点,
∴△ABC的面积=2△ABD的面积,
∴菱形ADBF的面积=△ABC的面积=40,
∴AB•AC=40,
∴×8•AC=40,
∴AC=10,
∴AC的长为10.
40.(2022•滨州)如图,菱形ABCD的边长为10,∠ABC=60°,对角线AC、BD相交于点O,点E在对角线BD上,连接AE,作∠AEF=120°且边EF与直线DC相交于点F.
(1)求菱形ABCD的面积;
(2)求证AE=EF.
【分析】(1)根据锐角三角函数可以求得BC边上的高,然后根据菱形的面积=底×高,即可求得相应的面积;
(2)连接EC,然后可以得到AE=EC,再根据四边形内角和,可以求得∠ECF=∠EFC,然后通过等量代换,即可证明结论成立.
【解答】(1)解:作AG⊥BC交BC于点G,如图所示,
∵四边形ABCD是菱形,边长为10,∠ABC=60°,
∴BC=10,AG=AB•sin60°=10×=5,
∴菱形ABCD的面积是:BC•AG=10×5=50,
即菱形ABCD的面积是50;
(2)证明:连接EC,
∵四边形ABCD是菱形,∠ABC=60°,
∴EO垂直平分AC,∠BCD=120°,
∴EA=EC,∠DCA=60°,
∴∠EAC=∠ECA,∠ACF=120°,
∵∠AEF=120°,
∴∠EAC+∠EFC=360°﹣∠AEF﹣∠ACF=360°﹣120°﹣120°=120°,
∵∠ECA+∠ECF=120°,
∴∠EFC=∠ECF,
∴EC=EF,
∴AE=EF.
41.(2022•南充)如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
求证:(1)△ADE≌△CDF.
(2)ME=NF.
【分析】(1)根据菱形的性质和全等三角形的判定SAS,可以证明结论成立;
(2)根据(1)中的结论和等腰三角形的性质,可以得到DE=DF,DM=DN,从而可以得到ME=NF.
【解答】证明:(1)∵四边形ABCD是菱形,
∴DA=DC,∠DAE=∠DCF,AB=CB,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS);
(2)由(1)知△ADE≌△CDF,
∴∠ADM=∠CDN,DE=DF,
∵四边形ABCD是菱形,
∴∠DAM=∠DCN,
∴∠DMA=∠DNC,
∴∠DMN=∠DNM,
∴DM=DN,
∴DE﹣DM=DF﹣DN,
∴ME=NF.
42.(2022•德阳)如图,在菱形ABCD中,∠ABC=60°,AB=2cm,过点D作BC的垂线,交BC的延长线于点H.点F从点B出发沿BD方向以2cm/s向点D匀速运动,同时,点E从点H出发沿HD方向以1cm/s向点D匀速运动.设点E,F的运动时间为t(单位:s),且0<t<3,过F作FG⊥BC于点G,连结EF.
(1)求证:四边形EFGH是矩形;
(2)连结FC,EC,点F,E在运动过程中,△BFC与△DCE是否能够全等?若能,求出此时t的值;若不能,请说明理由.
【分析】(1)根据平行线的判定定理得到EH∥FG,由题意知BF=2tcm,EH=tcm,推出四边形EFGH是平行四边形,根据矩形的判定定理即可得到四边形EFGH是矩形;
(2)根据菱形的性质得到∠ABC=60°,AB=2cm,求得∠ADC=∠ABC=60°,CD=AB=2cm,解直角三角形即可得到结论.
【解答】(1)证明:∵EH⊥BC,FG⊥BC,
∴EH∥FG,
由题意知BF=2tcm,EH=tcm,
∵在菱形ABCD中,∠ABC=60°,
∴∠CBD=30°,
∴FG=BF=t,
∴EH=FG,
∴四边形EFGH是平行四边形,
∵∠FGH=90°,
∴四边形EFGH是矩形;
(2)△BFC与△DCE能够全等,
理由:∵在菱形ABCD中,∠ABC=60°,AB=2cm,
∴∠ADC=∠ABC=60°,CD=AB=2cm,AB∥CD,
∴∠CBD=∠CDB=30°,∠DCH=∠ABC=60°,
∵DH⊥BC,
∴∠CHD=90°,
∴∠CDH=90°﹣60°=30°=∠CBF,
在Rt△CDH中,cs∠CDH=,
∴DH=2×=3,
∵BF=2tcm,
∴EH=tcm,
∴DE=(3﹣t)cm,
∴当BF=DE时,△BFC≌△DCE,
∴2t=3﹣t,
∴t=1.
43.(2022•遂宁)如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF∥AC交OE的延长线于点F,连接AF.
(1)求证:△AOE≌△DFE;
(2)判定四边形AODF的形状并说明理由.
【分析】(1)利用全等三角形的判定定理即可.
(2)先证明四边形AODF为平行四边形,再结合∠AOD=90°,即可得出结论.
【解答】(1)证明:∵E是AD的中点,
∴AE=DE,
∵DF∥AC,
∴∠OAD=∠ADF,
∵∠AEO=∠DEF,
∴△AOE≌△DFE(ASA).
(2)解:四边形AODF为矩形.
理由:∵△AOE≌△DFE,
∴AO=DF,
∵DF∥AC,
∴四边形AODF为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
即∠AOD=90°,
∴平行四边形AODF为矩形.
44.(2022•苏州)如图,将矩形ABCD沿对角线AC折叠,点B的对应点为点E,AE与CD交于点F.
(1)求证:△DAF≌△ECF;
(2)若∠FCE=40°,求∠CAB的度数.
【分析】(1)根据AAS证明三角形全等即可;
(2)利用全等三角形的性质,三角形内角和定理求解即可.
【解答】(1)证明:将矩形ABCD沿对角线AC折叠,则AD=BC=EC,∠D=∠B=∠E=90°,
在△DAF和△ECF中,
,
∴△DAF≌△ECF(AAS);
(2)∵△DAF≌△ECF,
∴∠DAF=∠ECF=40°,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠EAB=∠DAB﹣∠DAF=90°﹣40°=50°,
∵∠EAC=∠CAB,
∴∠CAB=25°.
45.(2022•丽水)如图,将矩形纸片ABCD折叠,使点B与点D重合,点A落在点P处,折痕为EF.
(1)求证:△PDE≌△CDF;
(2)若CD=4cm,EF=5cm,求BC的长.
【分析】(1)根据ASA证明两个三角形全等即可;
(2)如图,过点E作EG⊥BC于G,由勾股定理计算FG=3,设CF=x,在Rt△CDF中,由勾股定理得:DF2=CD2+CF2,列方程可解答.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=∠B=∠C=90°,AB=CD,
由折叠得:AB=PD,∠A=∠P=90°,∠B=∠PDF=90°,
∴PD=CD,
∵∠PDF=∠ADC,
∴∠PDE=∠CDF,
在△PDE和△CDF中,
,
∴△PDE≌△CDF(ASA);
(2)解:如图,过点E作EG⊥BC于G,
∴∠EGF=90°,EG=CD=4,
在Rt△EGF中,由勾股定理得:FG==3,
设CF=x,
由(1)知:PE=AE=BG=x,
∵AD∥BC,
∴∠DEF=∠BFE,
由折叠得:∠BFE=∠DFE,
∴∠DEF=∠DFE,
∴DE=DF=x+3,
在Rt△CDF中,由勾股定理得:DF2=CD2+CF2,
∴x2+42=(x+3)2,
∴x=,
∴BC=2x+3=+3=(cm).
46.(2022•自贡)如图,用四根木条钉成矩形框ABCD,把边BC固定在地面上,向右边推动矩形框,矩形的形状会发生改变(四边形具有不稳定性).
(1)通过观察分析,我们发现图中线段存在等量关系,如线段EB由AB旋转得到,所以EB=AB.我们还可以得到FC= CD ,EF= AD ;
(2)进一步观察,我们还会发现EF∥AD,请证明这一结论;
(3)已知BC=30cm,DC=80cm,若BE恰好经过原矩形DC边的中点H,求EF与BC之间的距离.
【分析】(1)由推动矩形框时,矩形ABCD的各边的长度没有改变,可求解;
(2)通过证明四边形BEFC是平行四边形,可得结论;
(3)由勾股定理可求BH的长,由相似三角形的性质可求解.
【解答】(1)解:∵把边BC固定在地面上,向右边推动矩形框,矩形的形状会发生改变,
∴矩形ABCD的各边的长度没有改变,
∴AB=BE,EF=AD,CF=CD,
故答案为:CD,AD;
(2)证明:∵四边形ABCD是矩形,
∴AD∥BC,AB=CD,AD=BC,
∵AB=BE,EF=AD,CF=CD,
∴BE=CF,EF=BC,
∴四边形BEFC是平行四边形,
∴EF∥BC,
∴EF∥AD;
(3)如图,过点E作EG⊥BC于G,
∵DC=AB=BE=80cm,点H是CD的中点,
∴CH=DH=40cm,
在Rt△BHC中,BH===50(cm),
∵EG⊥BC,
∴CH∥EG,
∴△BCH∽△BGE,
∴,
∴=,
∴EG=64,
∴EF与BC之间的距离为64cm.
47.(2022•湖州)如图,已知在Rt△ABC中,∠C=Rt∠,D是AB边上一点,以BD为直径的半圆O与边AC相切,切点为E,过点O作OF⊥BC,垂足为F.
(1)求证:OF=EC;
(2)若∠A=30°,BD=2,求AD的长.
【分析】(1)连接OE,由切线的性质可证明OE⊥AC,根据有三个角是直角的四边形OECF是矩形,可得结论;
(2)根据含30°角的直角三角形的性质可得AO的长,由线段的差可得答案.
【解答】(1)证明:连接OE,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠OEC=90°,
∵OF⊥BC,
∴∠OFC=90°,
∴∠OFC=∠C=∠OEC=90°,
∴四边形OECF是矩形,
∴OF=EC;
(2)解:∵BD=2,
∴OE=1,
∵∠A=30°,OE⊥AC,
∴AO=2OE=2,
∴AD=AO﹣OD=2﹣1=1.
48.(2022•湖州)已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.
(1)如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1,正方形BGFC的面积为S2.
①若S1=9,S2=16,求S的值;
②延长EA交GB的延长线于点N,连结FN,交BC于点M,交AB于点H.若FH⊥AB(如图2所示),求证:S2﹣S1=2S.
(2)如图3,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1,等边三角形CBE的面积为S2.以AB为边向上作等边三角形ABF(点C在△ABF内),连结EF,CF.若EF⊥CF,试探索S2﹣S1与S之间的等量关系,并说明理由.
【分析】(1)①由S1=9,S2=16,求得b=3,a=4,进而求出S=ab=6;
②先证明△AFN∽△NAB,得出,进而得出ab+b2=a2,即可证明S2﹣S1=2S;
(2)先证明△ABC≌△FBE(SAS),得出AC=FE=b,∠FEB=∠ACB=90°,求出∠FEC=30°,利用三角函数得出b=a,进而得出S=ab=a2,利由等边三角形的性质求出,,通过计算得出S2﹣S1=×,即可证明S2﹣S1=S.
【解答】(1)①解:∵S1=9,S2=16,
∴b=3,a=4,
∵∠ACB=90°,
∴S=ab==6;
②证明:由题意得:∠FAN=∠ANB=90°,
∴∠FAH+∠NAB=90°,
∵FH⊥AB,
∴∠FAH+∠AFN=90°,
∴∠AFN=∠NAB,
∴△AFN∽△NAB,
∴,即,
∴ab+b2=a2,
∴2S+S1=S2,
∴S2﹣S1=2S;
(2)解:S2﹣S1=S,
理由:∵△ABF和△CBE都是等边三角形,
∴AB=FB,CB=EB,∠ABF=∠CBE=60°,
∴∠ABF﹣∠CBF=∠CBE﹣∠CBF,
∴∠ABC=∠FBE,
在△ABC和△FBE中,
,
∴△ABC≌△FBE(SAS),
∴AC=FE=b,∠FEB=∠ACB=90°,
∴∠FEC=90°﹣60°=30°,
∵EF⊥CF,CE=BC=a,
∴sin∠FEC=,即sin30°=,
∴b=asin30°=a,
∴S=ab=a2,
∵△ACD和△CBE都是等边三角形,
∴,,
∴S2﹣S1==﹣==×,
∴S2﹣S1=S.
49.(2022•杭州)在正方形ABCD中,点M是边AB的中点,点E在线段AM上(不与点A重合),点F在边BC上,且AE=2BF,连接EF,以EF为边在正方形ABCD内作正方形EFGH.
(1)如图1,若AB=4,当点E与点M重合时,求正方形EFGH的面积.
(2)如图2,已知直线HG分别与边AD,BC交于点I,J,射线EH与射线AD交于点K.
①求证:EK=2EH;
②设∠AEK=α,△FGJ和四边形AEHI的面积分别为S1,S2.求证:=4sin2α﹣1.
【分析】(1)由点M是边AB的中点,若AB=4,当点E与点M重合,得出AE=BE=2,由AE=2BF,得出BF=1,由勾股定理得出EF2=5,即可求出正方形EFGH的面积;
(2)①由“一线三直角”证明△AKE∽△BEF,得出,由AE=2BF,得出,进而证明EK=2EH;
②先证明△KHI≌△FGJ,得出S△KHI=S△FGJ=S1,再证明△KAE∽△KHI,得出==,由正弦的定义得出sinα=,进而得出sin2α=,得出=4sin2α,即可证明=4sin2α﹣1.
【解答】(1)解:如图1,
∵点M是边AB的中点,若AB=4,当点E与点M重合,
∴AE=BE=2,
∵AE=2BF,
∴BF=1,
在Rt△EBF中,EF2=EB2+BF2=22+12=5,
∴正方形EFGH的面积=EF2=5;
(2)如图2,
①证明:
∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴∠K+∠AEK=90°,
∵四边形EFGH是正方形,
∴∠KEF=90°,EH=EF,
∴∠AEK+∠BEF=90°,
∴∠AKE=∠BEF,
∴△AKE∽△BEF,
∴,
∵AE=2BF,
∴,
∴EK=2EF,
∴EK=2EH;
②证明:∵四边形ABCD是正方形,
∴AD∥BC,
∴∠KIH=∠GJF,
∵四边形EFGH是正方形,
∴∠IHK=∠EHG=∠HGF=∠FGJ=90°,EH=FG,
∵KE=2EH,
∴EH=KH,
∴KH=FG,
在△KHI和△FGJ中,
,
∴△KHI≌△FGJ(AAS),
∴S△KHI=S△FGJ=S1,
∵∠K=∠K,∠A=∠IHK=90°,
∴△KAE∽△KHI,
∴==,
∵sinα=,
∴sin2α=,
∴=4sin2α,
∴=4sin2α﹣1.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2022/6/27 11:27:28;用户:账号1;邮箱:yzsysx1@xyh.cm;学号:2567002小惠:
证明:∵AC⊥BD,OB=OD,
∴AC垂直平分BD.
∴AB=AD,CB=CD,
∴四边形ABCD是菱形.
小洁:
这个题目还缺少条件,需要补充一个条件才能证明.
2022年中考数学必刷真题考点分类专练(全国通用) 专题18矩形菱形正方形(共49题)【原卷版+解析】: 这是一份2022年中考数学必刷真题考点分类专练(全国通用) 专题18矩形菱形正方形(共49题)【原卷版+解析】,共70页。
专题18 矩形菱形正方形(共39题)-2023年全国各地中考数学真题分项汇编(全国通用): 这是一份专题18 矩形菱形正方形(共39题)-2023年全国各地中考数学真题分项汇编(全国通用),文件包含专题18矩形菱形正方形共39题原卷版docx、专题18矩形菱形正方形共39题解析版docx等2份试卷配套教学资源,其中试卷共59页, 欢迎下载使用。
专题18 矩形菱形正方形(共39题)-备战2024年数学中考之真题分项汇编(全国通用): 这是一份专题18 矩形菱形正方形(共39题)-备战2024年数学中考之真题分项汇编(全国通用),文件包含专题18矩形菱形正方形共39题原卷版docx、专题18矩形菱形正方形共39题解析版docx等2份试卷配套教学资源,其中试卷共59页, 欢迎下载使用。