

人教版七年级数学下册同步精讲精练七年级下学期数学期中质量检测卷(测试范围:第五章---第七章)(原卷版+解析)
展开(测试范围:第五章---第七章)
(考试时间120分钟 满分120分)
选择题(共10题,每小题3分,共30分)
(2022秋•二七区校级期末)在实数3−27,,π,34,227,8,32,0.1010010001中,无理数
有( )
A.2个B.3个C.4个D.5个
2.(2022秋•和平区期末)在平面直角坐标系中,下列各点在第二象限的是( )
A.(﹣1,2)B.(﹣3,0)C.(0,4)D.(5,﹣6)
3.(2022春•宾阳县期中)下列计算正确的是( )
A.4=±2B.(−3)2=−3C.179=79D.3−8=−2
4.(2022•杭州模拟)下列说法中,正确的有( )个.
①过直线外一点作直线的垂线段,叫做点到直线的距离;
②过一点有且只有一条直线与已知直线平行;
③两条直线被第三条直线所截,内错角相等;
④对顶角相等;
⑤同一平面内,两条直线的位置关系有:相交,垂直和平行三种;
⑥平行于同一条直线的两条直线平行.
A.2B.3C.4D.5
5.(2022春•辛集市期末)如图,直线AB,CD相交于点O,OF⊥OC于O,OE平分∠AOF,如果∠COE=15°,那么∠BOD的度数是( )
A.75°B.50°C.60°D.70°
6.(2022秋•郫都区校级期末)如图,点E在BC的延长线上,下列条件不能判定AB∥CD的是( )
A.∠2=∠4B.∠B=∠5
C.∠5=∠DD.∠D+∠DAB=180°
7.(2022秋•阜阳期中)在平面直角坐标系中,点M(m﹣1,2m)在x轴上,则点M的坐标是( )
A.(1,0)B.(﹣1,0)C.(0,2)D.(0,﹣1)
8.(2022春•藤县期中)若实数a、b满足x−3+|y2−1|=0,则x+y的值为( )
A.4B.2C.2D.2或2
9.(2022秋•大渡口区校级期末)如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=( )
A.70°B.75°C.80°D.85°
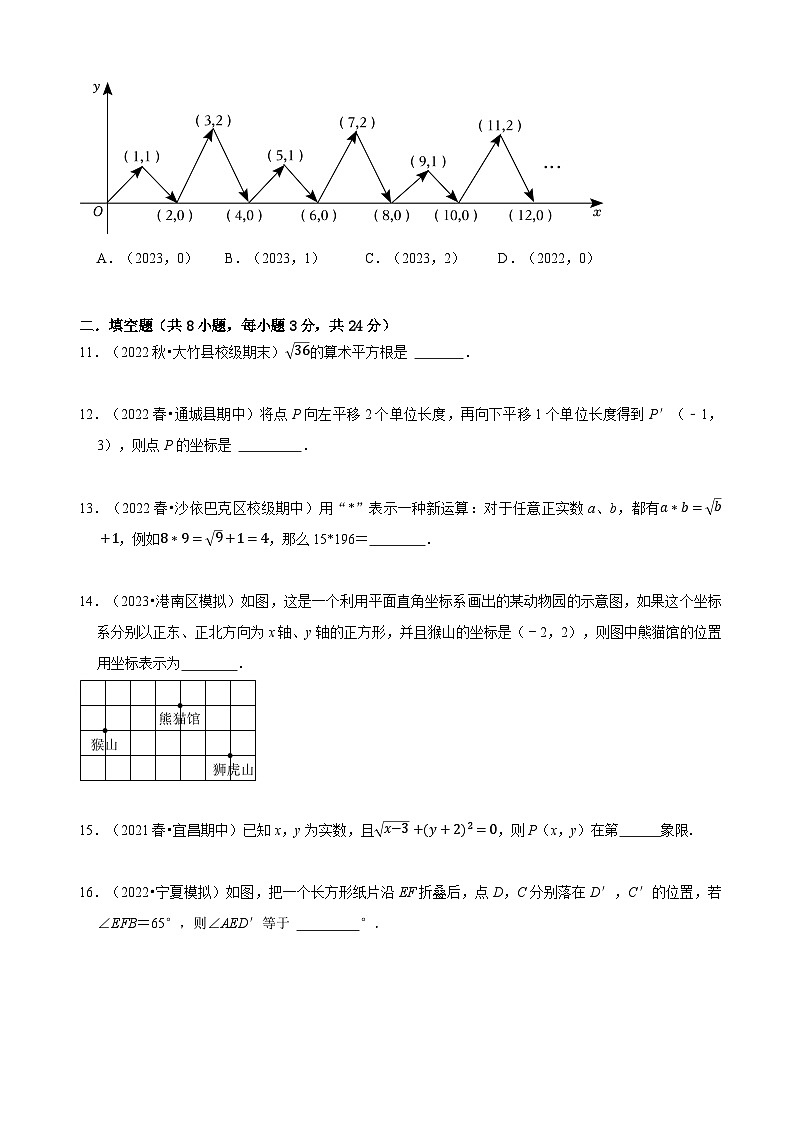
(2022秋•沭阳县期末)如图,动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),…,按这样的运动规律,则第2023次运动到
点( )
A.(2023,0)B.(2023,1)C.(2023,2)D.(2022,0)
填空题(共8小题,每小题3分,共24分)
11.(2022秋•大竹县校级期末)36的算术平方根是 .
12.(2022春•通城县期中)将点P向左平移2个单位长度,再向下平移1个单位长度得到P′(﹣1,3),则点P的坐标是 .
13.(2022春•沙依巴克区校级期中)用“*”表示一种新运算:对于任意正实数a、b,都有a∗b=b+1,例如8∗9=9+1=4,那么15*196= .
14.(2023•港南区模拟)如图,这是一个利用平面直角坐标系画出的某动物园的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方形,并且猴山的坐标是(﹣2,2),则图中熊猫馆的位置用坐标表示为 .
15.(2021春•宜昌期中)已知x,y为实数,且x−3+(y+2)2=0,则P(x,y)在第 象限.
16.(2022•宁夏模拟)如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于 °.
17.(2021秋•拱墅区校级期中)已知m,n分别是17的整数部分和小数部分,那么2m﹣n+17的值是 .
18.(2022春•东湖区校级月考)如图,直线EF上有两点A、C,分别引两条射线AB、CD,∠DCF=60°,∠EAB=70°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,在射线CD转动一周的时间内,使得CD与AB平行所有满足条件的时间= .
解答题(本大题共8小题,满分共66分)
19.(8分)(2022春•源汇区校级期中)计算题
(1)9−(−1)2021−327+|1−2| (2)(﹣2)3×(−4)2+3(−8)3×(−12)−327
20.(6分)(2022秋•晋江市期中)已知2a﹣1的平方根是±3,3a+b+10的立方根是3.
(1)求a,b的值;
(2)求a+b的算术平方根.
21.(7分)(2021秋•围场县期末)如图所示,直线AB,CD相交于点O,OE平分∠AOD,射线OF在∠BOD内部.
(1)若∠AOC=56°,求∠BOE的度数.
(2)若∠EOD:∠FOD:∠FOB=7:3:1,求∠COE的度数.
22.(7分)(2022春•河东区期中)在平面直角坐标系中,已知点M(2﹣m,1+2m).
(1)若点M到y轴的距离是3,求M点的坐标;
(2)若点M在第一、三象限的角平分线上,求M点的坐标.
23.(8分)如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别是A(4,2),B(1,0),C(5,﹣3),三角形ABC中任意一点P(x0,y0),经平移后对应点为P'(x0﹣6,y0+2),将三角形ABC作同样的平移得到三角形A'B'C',点A,B,C的对应点分别为A',B',C'.
(1)点A'的坐标为 ,点B'的坐标为 ;
(2)①画出三角形A'B'C';
②求出三角形A'B'C'的面积;
(3)过点A'作A'D∥y轴,交B'C'于点D,则点D的坐标为 .
24.(8分)(2022春•泗水县期中)如图,已知EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C.
(1)求证:AB∥MN;
(2)若∠BMN=140°,∠ADM=25°,求∠BAD的度数.
25.(10分)(2022春•陆丰市期末)如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+c−4=0.
(1)求a,b,c的值.
(2)求四边形AOBC的面积.
(3)是否存在点P(x,−12x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
26.(12分)(2022春•通城县期中)【阅读理解】题目:如图①,∠ABE和∠DCE的边AB与CD互相平行,边BE与CE交于点E.若∠ABE=140°,∠DCE=120°,求∠BEC的度数.
老师在黑板中写出了部分求解过程,请你完成下面的求解过程,并填空(理由或数学式).
解:如图②,过点E作EF∥AB.
∴∠BEF+∠ABE=180°( ).
∵∠ABE=140°,
∴∠BEF=180°﹣∠ABE=180°﹣140°=40°.
∵AB∥CD,
∴EF∥CD( ).
∴∠CEF+( )=180°.
∴∠DCE=120°,
∴∠CEF=180°﹣∠DCE=180°﹣120°=60°.
∴∠BEC=∠BEF+∠CEF=( )°.
【问题迁移】如图③,D、E分别是∠ABC边AB、BC上的点,在直线DE的右侧作DE的平行线分别交边BC、AB于点F、G.P是线段DG上一点,连结PE、PF.若∠DEP=40°,∠GFP=30°,求∠EPF的度数.
【拓展应用】如图④,D、E分别是∠ABC边AB、BC上的点,在直线DE的右侧作DE的平行线分别交边BC、AB于点F、G.P是射线DG上一点,连结PE、PF.若∠DEP=α,∠GFP=β,直接写出∠EPF与α、β之间的数量关系.
2022-2023学年七年级下学期数学
期中质量检测卷
(测试范围:第五章---第七章)
(考试时间120分钟 满分120分)
选择题(共10题,每小题3分,共30分)
(2022秋•二七区校级期末)在实数3−27,,π,34,227,8,32,0.1010010001中,无理数
有( )
A.2个B.3个C.4个D.5个
【分析】根据无理数的定义即可求解.
【解答】解:3−27=−3,
所以无理数有π,34,8,32,共4个.
故选:C.
【点评】本题主要考查了无理数的定义,熟练掌握无限不循环小数是无理数是解题的关键.
2.(2022秋•和平区期末)在平面直角坐标系中,下列各点在第二象限的是( )
A.(﹣1,2)B.(﹣3,0)C.(0,4)D.(5,﹣6)
【分析】根据第二象限内点的坐标特点解答即可.
【解答】解:∵第二象限内点的横坐标小于0,纵坐标大于0,
∴四个选项中只有(﹣1,2)符合.
故选:A.
【点评】本题考查的是点的坐标,熟知各象限内点的坐标特点是解题的关键.
3.(2022春•宾阳县期中)下列计算正确的是( )
A.4=±2B.(−3)2=−3C.179=79D.3−8=−2
【分析】根据算术平方根、平方根、立方根的定义解决此题.
【解答】解:A.根据算术平方根的定义,4=2,那么A错误,故A不符合题意.
B.根据乘方以及算术平方根的定义,(−3)2=3,那么B错误,故B不符合题意.
C.根据算术平方根的定义,179=169=43,那么C错误,故C不符合题意.
D.根据立方根的定义,3−8=−2,那么D正确,故D符合题意.
故选:D.
【点评】本题主要考查算术平方根、平方根、立方根,熟练掌握算术平方根、平方根、立方根的定义是解决本题的关键.
4.(2022•杭州模拟)下列说法中,正确的有( )个.
①过直线外一点作直线的垂线段,叫做点到直线的距离;
②过一点有且只有一条直线与已知直线平行;
③两条直线被第三条直线所截,内错角相等;
④对顶角相等;
⑤同一平面内,两条直线的位置关系有:相交,垂直和平行三种;
⑥平行于同一条直线的两条直线平行.
A.2B.3C.4D.5
【分析】根据垂线的性质、平行公理、平行线的性质、以及平行线的定义、对顶角的性质判断即可.
【解答】解:①垂线段是图形,而距离是数量,定义不准确,故①错误;
②过直线外一点有且只有一条直线与已知直线平行,缺少条件“外一点”故②错误;
③两条平行线被第三条直线所截,内错角相等,缺少条件“两直线平行”,故③错误;
④对顶角相等,教材定理,故④正确;
⑤同一平面内,两条直线的位置关系有:相交和平行两种,垂直属于相交的特殊情况,故⑤错误;
⑥平行于同一条直线的两条直线平行,教材定理,故⑥正确;
正确的有:④⑥,共2个.
故选:A.
【点评】此题考查了垂线的性质、平行公理、平行线的性质、以及平行线的定义、对顶角的性质等知识,掌握相关基础知识是解题的关键.
5.(2022春•辛集市期末)如图,直线AB,CD相交于点O,OF⊥OC于O,OE平分∠AOF,如果∠COE=15°,那么∠BOD的度数是( )
A.75°B.50°C.60°D.70°
【分析】根据垂直的定义得∠COF=90°,根据角平分线的定义得∠AOE=∠EOF,由∠COE=15°可求出∠AOE=∠EOF=75°,可得∠AOC=∠AOE﹣∠COE=60°,根据对顶角相等即可解答.
【解答】解:∵OF⊥OC,
∴∠COF=90°,
∵OE平分∠AOF,
∴∠AOE=∠EOF,
∵∠COE=15°,
∴∠AOE=∠EOF=∠COF﹣∠COE=75°,
∴∠AOC=∠AOE﹣∠COE=60°,
∴∠BOD=∠AOC=60°.
故选:C.
【点评】本题考查了垂线、角平分线、对顶角,熟记概念并准确识图是解题的关键.
6.(2022秋•郫都区校级期末)如图,点E在BC的延长线上,下列条件不能判定AB∥CD的是( )
A.∠2=∠4B.∠B=∠5
C.∠5=∠DD.∠D+∠DAB=180°
【分析】根据平行线的判定定理“同位角相等,两直线平行”、“内错角相等,两直线平行”、“同旁内角互补,两直线平行”分别进行分析.
【解答】解:A、根据内错角相等,两直线平行可判定AB∥CD,故此选项不合题意;
B、根据同位角相等,两直线平行可判定AB∥CD,故此选项不合题意;
C、根据内错角相等,两直线平行可判定AD∥CB,无法判定AB∥CD,故此选项符合题意;
D、根据同旁内角互补,两直线平行可判定AB∥CD,故此选项不合题意;
故选:C.
【点评】此题主要考查了平行线的判定,关键是掌握平行线的判定定理.
7.(2022秋•阜阳期中)在平面直角坐标系中,点M(m﹣1,2m)在x轴上,则点M的坐标是( )
A.(1,0)B.(﹣1,0)C.(0,2)D.(0,﹣1)
【分析】根据x轴上的点的纵坐标为0,得出m的值进而得出M的坐标.
【解答】解:点M(m﹣1,2m)在x轴上,则2m=0,
解得m=0,
∴M(﹣1,0),
故选:B.
【点评】本题考查了x轴上的点的坐标特征,掌握x轴上的点的纵坐标为0是解题的关键.
8.(2022春•藤县期中)若实数a、b满足x−3+|y2−1|=0,则x+y的值为( )
A.4B.2C.2D.2或2
【分析】根据非负数的性质“两个非负数相加和为0,这两个非负数的值都为0”解出x、y的值,进而求得代数式的值.
【解答】解:根据题意得:x﹣3=0,y2﹣1=0,
解得x=3,y=±1,
则x+y=3+1=4或x+y=3﹣1=2.
所以x+y的值为2或2.
故选:D.
【点评】本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.
9.(2022秋•大渡口区校级期末)如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=( )
A.70°B.75°C.80°D.85°
【分析】如图,作EF∥AB.利用平行线的性质得∠B+∠BEF=180°,∠C=∠CEF,即可解决问题.
【解答】解:如图,作EF∥AB,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠B+∠BEF=180°,∠C=∠CEF,
∵∠ABE=125°,∠C=30°,
∴∠BEF=55°,∠CEF=30°,
∴∠BEC=55°+30°=85°.
故选:D.
【点评】本题考查平行线的性质,解题的关键是学会添加常用辅助线,构造平行线解决问题.
10.(2022秋•沭阳县期末)如图,动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),…,按这样的运动规律,则第2023次运动到点( )
A.(2023,0)B.(2023,1)C.(2023,2)D.(2022,0)
【分析】根据前几次运动的规律可知第4n次接着运动到点(4n,0),第4n+1次接着运动到点(4n+1,1),第4n+2次从原点运动到点(4n+2,0),第4n+3次接着运动到点(4n+3,2),根据规律求解即可.
【解答】解:由题意可知,第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),
第3次接着运动到点(3,2),
第4次从原点运动到点(4,0),
第5次接着运动到点(5,1),
第6次接着运动到点(6,0),
……
第4n次接着运动到点(4n,0),
第4n+1次接着运动到点(4n+1,1),
第4n+2次从原点运动到点(4n+2,0),
第4n+3次接着运动到点(4n+3,2),
∵2023÷4=505……3,
∴第2023次接着运动到点(2023,2),
故选:C.
【点评】本题考查了点的坐标规律型问题,解题的关键是根据点的坐标的变化得到规律,利用得到的规律解题.
填空题(共8小题,每小题3分,共24分)
11.(2022秋•大竹县校级期末)36的算术平方根是 .
【分析】根据平方根,算术平方根和立方根的定义解答即可.
【解答】解:36=6,36的算术平方根是6.
故答案为:6.
【点评】本题主要考查了算术平方根的概念的运用以及应用,难度不大,属于基本知识.
12.(2022春•通城县期中)将点P向左平移2个单位长度,再向下平移1个单位长度得到P′(﹣1,3),则点P的坐标是 .
【分析】根据点的坐标的平移规律可得答案.
【解答】解:将点P向左平移2个单位长度,再向下平移1个单位长度得到P′(﹣1,3),则点P的坐标是(﹣1+2,3+1),即(1,4),
故答案为:(1,4).
【点评】本题主要考查坐标与图形变化—平移,解题的关键是掌握点的坐标的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减.
13.(2022春•沙依巴克区校级期中)用“*”表示一种新运算:对于任意正实数a、b,都有a∗b=b+1,例如8∗9=9+1=4,那么15*196= .
【分析】根据“*”所代表的运算法则,将数据代入进行运算即可.
【解答】解:由题意得,15*196=196+1=15.
故答案为:15.
【点评】此题考查了实数的运算,解答本题关键是明确新定义的运算符号所代表的运算法则,属于基础题.
14.(2023•港南区模拟)如图,这是一个利用平面直角坐标系画出的某动物园的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方形,并且猴山的坐标是(﹣2,2),则图中熊猫馆的位置用坐标表示为 .
【分析】根据猴山(﹣2,2)确定坐标原点的位置,然后建立坐标系,进而可确定熊猫馆的位置.
【解答】解:如图所示:
熊猫馆的点的坐标是(1,3),
故答案为:(1,3).
【点评】此题主要考查了坐标确定位置,关键是正确建立坐标系.
15.(2021春•宜昌期中)已知x,y为实数,且x−3+(y+2)2=0,则P(x,y)在第 象限.
【分析】形如a、a2、|a|,我们称为非负数,若非负数之和为0,则非负数为0,由题意可得x−3=0,(y+2)2=0,可得x、y的值,进而可得P点所在的象限.
【解答】解:∵x,y为实数,x−3≥0,(y+2)2≥0,x−3+(y+2)2=0,
∴x−3=0,(y+2)2=0,
∴x﹣3=0,y+2=0,
∴x=3,y=﹣2,
∴P点的坐标为(3,﹣2),
∴P点在第四象限,
故答案为:四.
【点评】本题考查了学生对非负数之和的应用,以及对平面直角坐标系点所在象限的理解,综合性较强.
16.(2022•宁夏模拟)如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于 °.
【分析】先根据平行线的性质得出∠DEF的度数,再根据翻折变换的性质得出∠D′EF的度数,根据平角的定义即可得出结论.
【解答】解:∵AD∥BC,∠EFB=65°,
∴∠DEF=65°,
又∵∠DEF=∠D′EF=65°,
∴∠D′EF=65°,
∴∠AED′=180°﹣65°﹣65°=50°.
故答案是:50.
【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.
17.(2021秋•拱墅区校级期中)已知m,n分别是17的整数部分和小数部分,那么2m﹣n+17的值是 .
【分析】先估算出17的值的范围,从而求出m,n的值,然后代入式子中进行计算即可解答.
【解答】解:∵16<17<25,
∴4<17<5,
∴17的整数部分是4,小数部分是17−4,
∴m=4,n=17−4,
∴2m﹣n+17=2×4﹣(17−4)+17
=8−17+4+17
=12,
故答案为:12.
【点评】本题考查了估算无理数的大小,熟练掌握估算无理数的大小是解题的关键.
18.(2022春•东湖区校级月考)如图,直线EF上有两点A、C,分别引两条射线AB、CD,∠DCF=60°,∠EAB=70°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,在射线CD转动一周的时间内,使得CD与AB平行所有满足条件的时间= .
【分析】分①AB与CD在EF的两侧,分别表示出∠ACD与∠BAC,然后根据内错角相等两直线平行,列式计算即可得解;
②CD旋转到与AB都在EF的右侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解;
③CD旋转到与AB都在EF的左侧,分别表示出∠DCF与∠BAC,然后根据同位角相等两直线平行,列式计算即可得解.
【解答】解:∵∠EAB=70°,∠DCF=60°,
∴∠BAC=110°,∠ACD=120°,
分三种情况:
如图①,AB与CD在EF的两侧时,
∠ACD=120°﹣(3t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠ACD=∠BAC,
即120°﹣(3t)°=110°﹣t°,
解得t=5;
②CD旋转到与AB都在EF的右侧时,
∠DCF=360°﹣(3t)°﹣60°=300°﹣(3t)°,∠BAC=110°﹣t°,
要使AB∥CD,则∠DCF=∠BAC,
即300°﹣(3t)°=110°﹣t°,
解得t=95;
③CD旋转到与AB都在EF的左侧时,
∠DCF=(3t)°﹣(180°﹣60°+180°)=(3t)°﹣300°,∠BAC=t°﹣110°,
要使AB∥CD,则∠DCF=∠BAC,
即(3t)°﹣300°=t°﹣110°,
解得t=95,
∴此情况不存在.
综上所述,当时间t的值为5秒或95秒时,CD与AB平行.
故答案为:5秒或95秒.
【点评】本题考查了平行线的判定,读懂题意并熟练掌握平行线的判定方法是解题的关键,要注意分情况讨论.
解答题(本大题共8小题,满分共66分)
19.(8分)(2022春•源汇区校级期中)计算题
(1)9−(−1)2021−327+|1−2| (2)(﹣2)3×(−4)2+3(−8)3×(−12)−327
【分析】(1)根据算术平方根、乘方、立方根、绝对值的意义进行计算即可;
(2)根据立方、算术平方根、立方根的意义化简后,再进行有理数混合运算即可.
【解答】解:(1)9−(−1)2021−327+|1−2|
=3−(−1)−3+2−1
=3+1−3+2−1
=2;
(2)(−2)3×(−4)2+3(−8)3×(−12)−327
=−8×4+(−8)×(−12)−3
=﹣8×4+4﹣3
=﹣32+4﹣3
=﹣31.
【点评】本题主要考查了算术平方根、乘方、立方根、绝对值的意义等知识,掌握运算法则是解题的关键.
20.(6分)(2022秋•晋江市期中)已知2a﹣1的平方根是±3,3a+b+10的立方根是3.
(1)求a,b的值;
(2)求a+b的算术平方根.
【分析】(1)根据平方根和立方根的定义即可求出a,b的值;
(2)把a=5,b=2代入a﹣2b求出代数式的值,再求它的算术平方根即可.
【解答】解:(1)∵2a﹣1的平方根是±3,
∴2a﹣1=9,
∴a=5,
∵3a+b+10的立方根是3,
∴3a+b+10=27,
∴15+b+10=27,
∴b=2;
(2)把a=5,b=2代入a+b得:a+b=5+2=7,
a+b的算术平方根是7.
【点评】本题考查了平方根,立方根和算术平方根,注意平方根、立方根和平方、立方互为逆运算.
21.(7分)(2021秋•围场县期末)如图所示,直线AB,CD相交于点O,OE平分∠AOD,射线OF在∠BOD内部.
(1)若∠AOC=56°,求∠BOE的度数.
(2)若∠EOD:∠FOD:∠FOB=7:3:1,求∠COE的度数.
【分析】(1)根据对顶角得到性质得到∠BOD=∠AOC=56°,根据邻补角的性质得到∠AOD=180°﹣∠BOD=124°,根据角平分线的定义得到∠DOE=∠AOE=12∠AOD=62°,于是得到结论;
(2)根据角平分线的定义得到∠BOF=∠DOF=12∠BOD,∠AOE=∠DOE=12∠AOD,根据余角的性质即可得到答案.
【解答】解:(1)∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=56°,
∴∠AOD=180°﹣∠BOD=124°,
∵OE平分∠AOD,
∴∠DOE=∠AOE=12∠AOD=62°,
∴∠BOE=∠BOD+∠DOE=62°+56°=118°;
(2)∵OE平分∠AOD,
∴∠AOE=∠DOE,
∵∠EOD:∠FOD:∠FOB=7:3:1,
∴∠AOE:∠EOD:∠FOD:∠FOB=7:7:3:1,
∴∠AOE=77+7+3+1×180°=70°,∠BOD=47+7+3+1×180°=40°,
∵∠AOC=∠BOD=40°,
∴∠COE=∠AOC+∠AOE=40°+70°=110°.
【点评】本题考查了对顶角和邻补角,余角的性质,角平分线的定义,熟练掌握对顶角的性质是解题的关键.
22.(7分)(2022春•河东区期中)在平面直角坐标系中,已知点M(2﹣m,1+2m).
(1)若点M到y轴的距离是3,求M点的坐标;
(2)若点M在第一、三象限的角平分线上,求M点的坐标.
【分析】(1)根据M到y轴的距离为3,得到横坐标的绝对值为3,求出m的值即可;
(2)根据M在第一、三象限的角平分线上,得到M横纵坐标相等,求出m的值即可.
【解答】解:
(1)∵M(2﹣m,1+2m)到y轴的距离是3,
∴|2﹣m|=3,即2﹣m=3或2﹣m=﹣3,
解得m=﹣1或m=5;
当m=﹣1时,M点的坐标是(3,﹣1);
当m=5时,M点的坐标是(﹣3,11);
∴M点坐标是(3,﹣1),(﹣3,11).
(2)∵M(2﹣m,1+2m)在第一、三象限的角平分线上,
∴m﹣2=1+2m,
解得m=﹣3.
∴M点的坐标是(﹣5,﹣5)
【点评】此题主要考查了点的坐标性质,用到的知识点为:点到两坐标轴的距离相等,那么点的横纵坐标相等或互为相反数以及在坐标轴上的点的性质.
23.(8分)如图,在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别是A(4,2),B(1,0),C(5,﹣3),三角形ABC中任意一点P(x0,y0),经平移后对应点为P'(x0﹣6,y0+2),将三角形ABC作同样的平移得到三角形A'B'C',点A,B,C的对应点分别为A',B',C'.
(1)点A'的坐标为 ,点B'的坐标为 ;
(2)①画出三角形A'B'C';
②求出三角形A'B'C'的面积;
(3)过点A'作A'D∥y轴,交B'C'于点D,则点D的坐标为 .
【分析】(1)由平移的性质可得△ABC向左平移6个单位,向上平移2个单位,即可求解;
(2)①根据点的坐标画出图形即可;
②由面积的和差关系可求解;
(3)由三角形的面积公式可求解.
【解答】解:(1)∵三角形ABC中任意一点P(x0,y0),经平移后对应点为P'(x0﹣6,y0+2),
∴△ABC向左平移6个单位,向上平移2个单位,
∵三角形ABC三个顶点的坐标分别是A(4,2),B(1,0),C(5,﹣3),
∴点A'(﹣2,4),点B'(﹣5,2),点C'(﹣1,﹣1),
故答案为:(﹣2,4),(﹣5,2);
(2)①如图所示:
②△A'B'C'的面积=5×4−12×3×2−12×4×3−12×5×1=172;
(3)∵S△A'B'C'=12×A'D×4=172,
∴A'D=174,
∵点A'(﹣2,4),
∴点D(﹣2,−14),
故答案为:(﹣2,−14).
【点评】本题考查了坐标与图形变化﹣平移,考查了平移的性质,三角形的面积公式,灵活运用这些性质解决问题是解题的关键.
24.(8分)(2022春•泗水县期中)如图,已知EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C.
(1)求证:AB∥MN;
(2)若∠BMN=140°,∠ADM=25°,求∠BAD的度数.
【分析】(1)根据垂直定义可得∠CFE=∠CMD=90°,从而可得EF∥DM,然后利用平行线的性质可得∠2=∠CDM,从而可得∠1=∠CDM,再利用平行线的判定可得MN∥CD,从而利用平行线的性质可得∠C=∠AMN,最后利用等量代换可得∠3=∠AMN,再利用平行线的判定,即可解答;
(2)利用(1)的结论可求出∠B=40°,然后利用三角形内角和定理,进行计算即可解答.
【解答】解:(1)因为EF⊥AC,DB⊥AC,
∴∠CFE=∠CMD=90°(垂直定义),
∴EF∥DM(同位角相等,两直线平行),
∴∠2=∠CDM(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠1=∠CDM(等量代换),
∴MN∥CD(内错角相等,两直线平行),
∴∠C=∠AMN,(两直线平行,同位角相等),
因为∠3=∠C(已知),
∴∠3=∠AMN(等量代换),
∴AB∥MN(内错角相等,两直线平行);
(2)∵AB∥MN,
∴∠B=180°﹣∠BMN=40°,
∵∠ADM=25°,
∴∠BAD=180°﹣∠B﹣∠ADM=115°,
∴∠BAD的度数为115°.
【点评】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
25.(10分)(2022春•陆丰市期末)如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+c−4=0.
(1)求a,b,c的值.
(2)求四边形AOBC的面积.
(3)是否存在点P(x,−12x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
【分析】(1)根据“几个非负数相加和为0,则每一个非负数的值均为0”解出a,b,c的值;
(2)由点A、O、B、C的坐标可得四边形AOBC为直角梯形,根据直角梯形的面积公式计算即可;
(3)设存在点P(x,−12x),使△AOP的面积为四边形AOBC的面积的两倍.根据面积列出方程12×2×|x|=|x|=2×9,解方程即可.
【解答】解:(1)∵|a﹣2|+(b﹣3)2+c−4=0,
∴a﹣2=0,b﹣3=0,c﹣4=0,
∴a=2,b=3,c=4;
(2)∵A(0,2),O(0,0),B(3,0),C(3,4);
∴四边形AOBC为直角梯形,且OA=2,BC=4,OB=3,
∴四边形AOBC的面积=12×(OA+BC)×OB=12×(2+4)×3=9;
(3)设存在点P(x,−12x),使△AOP的面积为四边形AOBC的面积的两倍.
∵△AOP的面积=12×2×|x|=|x|,
∴|x|=2×9,
∴x=±18
∴存在点P(18,﹣9)或(﹣18,9),
使△AOP的面积为四边形AOBC的面积的两倍.
【点评】本题考查了坐标与图形性质,非负数的性质,梯形的面积,三角形的面积,难度适中.根据非负数的性质求出a,b,c的值是解题的关键.
26.(12分)(2022春•通城县期中)【阅读理解】题目:如图①,∠ABE和∠DCE的边AB与CD互相平行,边BE与CE交于点E.若∠ABE=140°,∠DCE=120°,求∠BEC的度数.
老师在黑板中写出了部分求解过程,请你完成下面的求解过程,并填空(理由或数学式).
解:如图②,过点E作EF∥AB.
∴∠BEF+∠ABE=180°( ).
∵∠ABE=140°,
∴∠BEF=180°﹣∠ABE=180°﹣140°=40°.
∵AB∥CD,
∴EF∥CD( ).
∴∠CEF+( )=180°.
∴∠DCE=120°,
∴∠CEF=180°﹣∠DCE=180°﹣120°=60°.
∴∠BEC=∠BEF+∠CEF=( )°.
【问题迁移】如图③,D、E分别是∠ABC边AB、BC上的点,在直线DE的右侧作DE的平行线分别交边BC、AB于点F、G.P是线段DG上一点,连结PE、PF.若∠DEP=40°,∠GFP=30°,求∠EPF的度数.
【拓展应用】如图④,D、E分别是∠ABC边AB、BC上的点,在直线DE的右侧作DE的平行线分别交边BC、AB于点F、G.P是射线DG上一点,连结PE、PF.若∠DEP=α,∠GFP=β,直接写出∠EPF与α、β之间的数量关系.
【分析】【阅读理解】:如图②,过点E作EF∥AB,根据推理步骤,写出理由;
【问题迁移】:如图,过点P作PQ∥DE,先求出∠EPQ=∠DEP=40°,再求∠FPQ=∠GFP=30°,得∠EPF=∠EPQ+∠FPQ=70°,
【拓展应用】当点P在线段DG上,过点P作PQ∥DE,先证明∠EPQ=∠DEP=α,再证明∠FPQ=∠GFP=β,得∠EPF=∠EPQ+∠FPQ=α+β,
当点P在线段DG的延长线上时,先证明∠FHE=∠DEP=α,已知∠EPF=∠FHE﹣∠PFA,得∠EPF=α﹣β.
【解答】解:【阅读理解】如图②,过点E作EF∥AB.
∴∠BEF+∠ABE=180°(两直线平行,同旁内角互补).
∵∠ABE=140°,
∴∠BEF=180°﹣∠ABE=180°﹣140°=40°.
∵AB∥CD(已知),
∴EF∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
∴∠CEF+(∠DCE )=180°.
∴∠DCE=120°,
∴∠CEF=180°﹣∠DCE=180°﹣120°=60°.
∴∠BEC=∠BEF+∠CEF=(100)°.
故答案为:两直线平行,同旁内角互补;已知;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;∠DCE;100;
【问题迁移】
如图,过点P作PQ∥DE,
∴∠EPQ=∠DEP=40°,
∵DE∥FG,
∴PQ∥FG,
∴∠FPQ=∠GFP=30°,
∴∠EPF=∠EPQ+∠FPQ=70°,
【拓展应用】当点P在线段DG上,
过点P作PQ∥DE,
∴∠EPQ=∠DEP=α,
∵DE∥FG
∴PQ∥FG,
∴∠FPQ=∠GFP=β,
∴∠EPF=∠EPQ+∠FPQ=α+β,
当点P在线段DG的延长线上时,
∴∠FHE=∠DEP=α,
∵∠EPF=∠FHE﹣∠PFA,
∴∠EPF=α﹣β,
∴∠EPF=α+β或∠EPF=α﹣β.
【点评】本题考查了平行线的性质与判定、三角形的外角性质、角的和差等知识;熟练掌握平行线的判定与性质,作出辅助平行线是解决问题的关键.
初中数学人教版七年级下册6.3 实数当堂检测题: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c77686_t7/?tag_id=28" target="_blank">6.3 实数当堂检测题</a>,共47页。试卷主要包含了3 实 数,7,237,π2,0,123456…,−32;,8282,2=10,等内容,欢迎下载使用。
初中数学人教版七年级下册第五章 相交线与平行线5.4 平移习题: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c10220_t7/?tag_id=28" target="_blank">第五章 相交线与平行线5.4 平移习题</a>,共47页。试卷主要包含了4 平 移等内容,欢迎下载使用。
人教版七年级数学下册同步精讲精练第一次月考检测试卷(测试范围:第五章和第六章)(原卷版+解析): 这是一份人教版七年级数学下册同步精讲精练第一次月考检测试卷(测试范围:第五章和第六章)(原卷版+解析),共23页。












