湖南省张家界市慈利县2023—2024学年九年级上学期期末考试数学试题

这是一份湖南省张家界市慈利县2023—2024学年九年级上学期期末考试数学试题，共8页。试卷主要包含了在中，，，，那么的正弦值是等内容，欢迎下载使用。
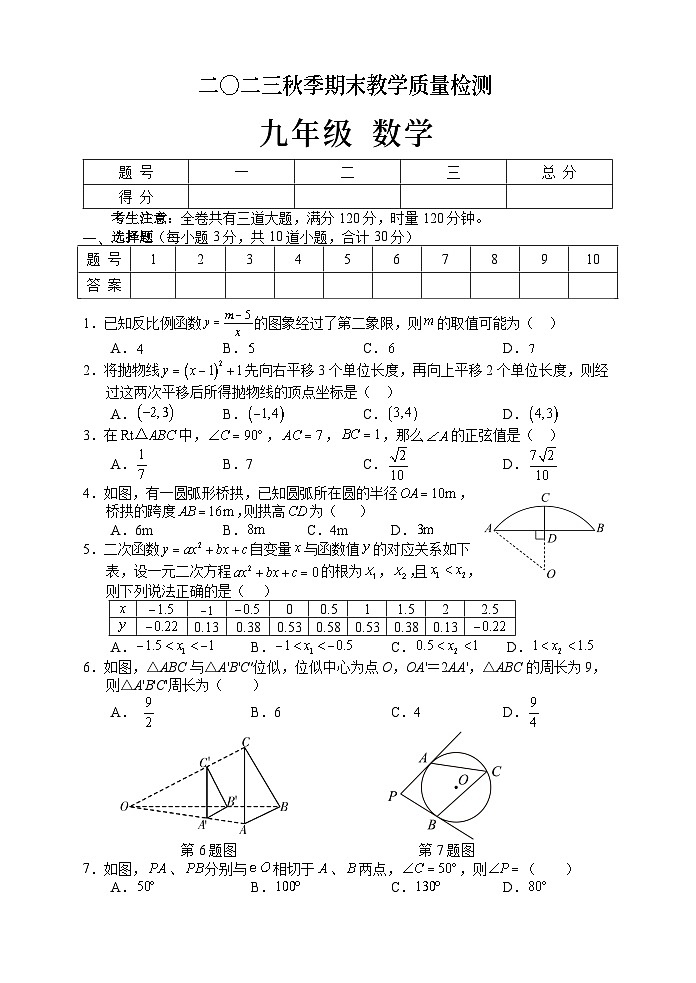
考生注意：全卷共有三道大题，满分120分，时量120分钟。
选择题（每小题3分，共10道小题，合计30分）
1．已知反比例函数的图象经过了第二象限，则的取值可能为（ ）
A．B．C．D．
2．将抛物线先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后所得抛物线的顶点坐标是（ ）
A．B．C．D．
3．在中，，，，那么的正弦值是（ ）
A．B．7C．D．
4．如图，有一圆弧形桥拱，已知圆弧所在圆的半径，桥拱的跨度，则拱高为（ ）
A．6mB．C．4m D．
5．二次函数自变量与函数值的对应关系如下表，设一元二次方程的根为，，且，则下列说法正确的是（ ）
A．B．C． D．
6．如图，△ABC与△A'B'C′位似，位似中心为点O，OA'＝2AA'，△ABC的周长为9，则△A'B'C'周长为（ ）
A． B．6C．4D．

第6题图 第7题图
7．如图，、分别与相切于、两点，，则（ ）
A．B．C．D．
8．已知关于的方程的两实数根为，，若，您看到的资料都源自我们平台，20多万份试卷，家威杏 MXSJ663 每日最新，性比价最高则的值为（ ）
A．B．C．或1D．或3
9．抛物线的对称轴为直线，其部分图象交x轴负半轴于点A，交y轴正半轴于点B，如图所示，则下列结论：
①；
②；
③（m为任意实数）；
④点是该抛物线上的点，且．
其中正确的有（ ）
A．①②③B．①②④C．①③④D．①②③④
10．如图，在平面直角坐标系中，点A，C分别在坐标轴上，且四边形是边长为3的正方形，反比例函数的图像与边分别交于两点，的面积为4，点P为y轴上一点，则的最小值为（ ）
A．3 B．C．D．5
二、填空题（本大题共8个小题，每小题 3 分，共24分）
11．已知，是方程的两个根，则数据：4，a，6，，7的平均数是 ．
12．已知，则的值为 .
13．已知点，，均在反比例函数的图象上，则，，的大小关系为 ．（请用“”连接）
14．用配方法解一元二次方程时，将它化为的形式，则的值为 ．
15．如果方程mx2+2x+1＝0有两个不相等的实数根，那么m的取值范围是 .
16．如图，扇形的半径为2，分别以点为圆心，大于的长为半径画弧，两弧相交于点P，，则的长 .（结果保留）
17．如图所示，在中，，是边上的中线，，，则的值是 ．

第16题图 第17题图 第18题图
18．如图，在△ABC中，D在AC边上，AD∶DC＝1∶2，O是BD的中点，连接AO并延长交BC于点E，若BE＝3，则EC的长为 ．
三、解答题（共计66分）
19．（6分）计算：．
20．（8分）一架无人机沿水平直线飞行进行测绘工作，在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°，面向AB方向继续飞行5米，测得该建筑物底端B的俯角为45°，已知建筑物AB的高为3米，求无人机飞行的高度(结果精确到1米，参考数据：1.414， 1.732)．
21．（8分）张家界某特产商店将进价为每件20元的礼盒的售价确定为每件40元．
（1）中秋期间，该商店进行降价促销活动，预备将原来售价进行两次降价，降价后该礼盒现价为32.4元．若该商品两次降价的降价率相同，求这个降价率；
（2）经调查，该商品每降价2元，即可多销售100件．已知该商品售价40元时每月可销售500件，若该商店希望该商品每月能盈利10000元，且尽可能扩大销售量，则该商品在原售价的基础上应如何调整？
22．（8分）县教育局为了了解某年级学生对科学知识的掌握情况，在全区范围内随机抽取若干名学生进行科学知识监测，按照测试成绩分优秀、良好、合格与不合格四个等级，并绘制了如下两幅不完整统计图．
（1）参与本次测试的学生人数为 ， ．
（2）请补全条形统计图．
（3）若全县该年级共有5000名学生，请估计该年级对科学知识掌握情况较好（测试成绩能达到良好及以上等级）的学生人数．
23．（8分）如图，在梯形中，点F，E分别在线段，上，且，
（1）求证：
（2）若，求证：
24．（8分）如图，以的边为直径作，交边于点D，为的切线，弦于点F，连接．
（1）求证：．
（2）若点F为中点，且，求线段的长．
25．（10分）如图，抛物线与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知，．
（1）求抛物线的表达式；
（2）点E是线段上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，的面积最大？求出的最大面积及此时E点的坐标；
（3）在坐标平面内是否存在点P，使得以A，C，D，P为顶点的四边形是平行四边形？如果存在，直接写出P点的坐标；如果不存在，请说明理由．
26．（10分）定义：有一组邻边相等且对角互补的四边形称为“等补四边形”．
（1）下列选项中一定是“等补四边形”的是________；
A．平行四边形；B．矩形；C．正方形；D．菱形
（2）如图1，在边长为a的正方形中，E为边上一动点（E不与C、D重合），交于点F，过F作交于点H．

图1 图2 备用图
①试判断四边形是否为“等补四边形”并说明理由；
②如图2，连接，将绕A点逆时针旋转得到，判断线段EH与线段EL的数量关系，并求的周长；
③若四边形是“等补四边形”，当a=3时，求的长．
二○二三年秋季期末教学质量检测
九年级数学参考答案
一、选择题（3分×10=30分）
二、填空题（3分×8=24分）
11．4 12．13． 14．
15．且 16．17．218．9
三、解答题
19．（6分）解：
4分(每计算对一个计1分）
． 6分
20．（8分）无人机飞行的高度约为14米．
解：如图，延长PQ，BA，相交于点E，
由题意可得：AB⊥PQ，∠E＝90°，
又∵∠BQE＝45°，分
∴BE＝QE， 分
设BE＝QE＝x，∵PQ＝5，AB＝3，
∴PE＝x＋5，AE＝x－3，∵∠E＝90°，
∴tan∠APE＝，分
∵∠APE＝30°，∴tan30°＝，分
解得：x＝≈14，分
答：无人机飞行的高度约为14米．
21．（8分）（1）这个降价率为10%；（2）该商品在原售价的基础上，再降低10元．
解：（1）设这个降价率是，依题意得， 分
解得（舍去）．分
答：这个降价率为10%．
（2）设降价元，则可多销售件，
根据题意得， 分
解得（舍去）或．
答：该商品在原售价的基础上，再降低10元．分
22．（8分）(1)150人，(2)补全图形见解析(3)3500人．
（1）解：（人），∴参与本次测试的学生人数为150人，分
，∴；分
故答案为：人；30；
（2）∵（人），分
补全图形如右：
（3）（人）；分
∴全区该年纪共有5000名学生，请估计该年级对科学知识掌握情况较好（测试成绩能达到良好及以上等级）的学生人数有3500人．
23．（8分）（1）证明见解析 （2）证明见解析
【详解】（1）证明：，
，分
在和中，，
，分
．分
（2）证明：，，
，即，分
在和中，，
，分
，由（1）已证：，，
．分
24．（8分））(1)见解析；(2)．
（1）证明：为直径，为的切线，
∴，分
∴，∵，∴，
∴， 分
∵，分
∴；分
（2）解：如图所示，连接，∵点F为中点，，
∴是线段的垂直平分线，分
∴，∴是等边三角形，
∴，分
∴，分
∵，∴．分
25．（1）；（2）有最大值为8，；
（3）存在，P点的坐标为或或．
【详解】（1）解：由题意，将，代入，
得，解得，
∴抛物线的表达式为； 分
（2）解：令，则，∴，
设直线的解析式为,
将B、C点坐标代入得，解得，
∴直线的解析式为，分
设，
轴于点H，则，
∴
， .
∴
分
∵是关于x的二次函数，，
∴当时，有最大值为8，分
此时；分
（3）解：解：由，可知对称轴为直线，
∴，∵，，设P点的坐标为，
①当为对角线时，，，
解得，，∴P点的坐标为；
②当为对角线时，
，，解得，，
∴P点的坐标为；
③当为对角线时，
，，解得，，
∴P点的坐标为；
综上，P点的坐标为或或．分（每写对一个得1分）
26．（1）C （2）①四边形是等补四边形，见解析；
②；③或者
（1）解：在平行四边形、矩形、正方形、菱形中，只有正方形的邻边相等且对角互补，
∴正方形是等补四边形，故选：D．分
（2）解：①四边形是“等补四边形”，理由如下：
∵为正方形的对角线，∴，又，，
∴A、B、H、F四点共圆，∴，∴，
∴，又，
∴四边形是“等补四边形”．分
②将绕A点逆时针旋转得到，
∴，，
∴E、D、L三点共线，
由①得，∴，
在和中
∴，
∴，分
∴的周长；分
③∵，四边形ECHF是“等补四边形”，
∴还需要一组邻边相等，分以下四种情况讨论：
情况1：，连接，
由题意知∶，，
又，∴，
∴，则为正三角形，
∴，∴，
∴，；
情况2：，则，
∴，同情况1，；
情况3：，由②得的周长．
设，则，有，
∴，即；
情况4：，连接，
则，则HF垂直平分AE，
∴，∵，，
∴，∵，，
∴，∴，∴，又，
∴，又，，
∴，∴，这不可能，故这种情况不存在．
综上：或者． 分(每对一种情况得1分）题 号
一
二
三
总 分
得 分
题 号
1
2
3
4
5
6
7
8
9
10
答 案
0
0.5
1
1.5
2
2.5
0.13
0.38
0.53
0.58
0.53
0.38
0.13
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
C
A
B
D
A
A
B