浙江省杭州市临平区2023-2024学年九年级上学期月考数学试卷（1月份）

这是一份浙江省杭州市临平区2023-2024学年九年级上学期月考数学试卷（1月份），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）2024的相反数是（ ）
A．2024B．﹣2024C．D．
2．（3分）记者从10月7日的杭州亚运会赛事总结新闻发布会上获悉，截至7日上午，杭州亚运会售票总数超过3050000张．将3050000这个数用科学记数法表示为（ ）
A．3.05×106B．30.5×105C．0.305×107D．3.05×107
3．（3分）估计的值在（ ）
A．6和7之间B．5和6之间C．4和5之间D．3和4之间
4．（3分）在下列各组单项式中，不是同类项的是（ ）
A．5x2y和﹣7x2yB．m2n和2mn2
C．﹣3和99D．﹣abc和9abc
5．（3分）实数abc在数轴上的对应点的位置如图所示，如果a+c＝0，那么下列结论正确的是（ ）
A．b＜0B．a＜﹣bC．ab＞0D．b﹣c＞0
6．（3分）下列方程变形正确的是（ ）
A．方程3x﹣2＝2x+1，移项，得3x﹣2x＝﹣1+2
B．方程3﹣x＝2﹣5（x﹣1），去括号，得3﹣x＝2﹣5x﹣1
C．方程，未知数系数化为1，得t＝2
D．方程化成
7．（3分）如图，AB，CD交于点O，OE平分∠AOD，∠COB＝140°，则∠BOE的度数为（ ）您看到的资料都源自我们平台，20多万份试卷，家威杏 MXSJ663 每日最新，性比价最高
A．40°B．70°C．110°D．130°
8．（3分）如图，大小两个正方形的边长分别是4和3，叠放在一起后两个阴影部分的面积分别为a，b（a＜b），则2a（a﹣1）﹣2（a2﹣b）的值为（ ）
A．2B．7C．14D．25
9．（3分）若一个长方形的周长为42，将它的长减少3，宽增加2，恰好得到一个正方形，设这个正方形的边长为x，根据题意可列方程为（ ）
A．x+3+x﹣2＝21B．x﹣3+x+2＝21
C．x+3+x﹣2＝42D．x﹣3＝（21﹣x）+2
10．（3分）下列说法正确的个数有（ ）
①一个四次多项式与一个五次多项式的和一定是一个五次整式．
②三条直线相交，有三个交点．
③连接两点间的线段，叫做这两点的距离．
④若有理数a和b互为相反数，则一定有a＝﹣b．
⑤若线段AB＝BC，则点B是线段AC的中点．
A．1个B．2个C．3个D．4个
二、填空题：本题有6个小题，每小题4分，共24分.
11．（4分）用四舍五入法把数1.3579精确到百分位，所得的近似数是 ．
12．（4分）在数轴上，若A点表示﹣3，在A点左侧到点A距离等于2的点所表示的数是 ．
13．（4分）如果x＝1是关于x的方程x﹣2m＝9的解，则m的值为 ．
14．（4分）两根木条，一根长10cm，另一根长8cm，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为 cm．
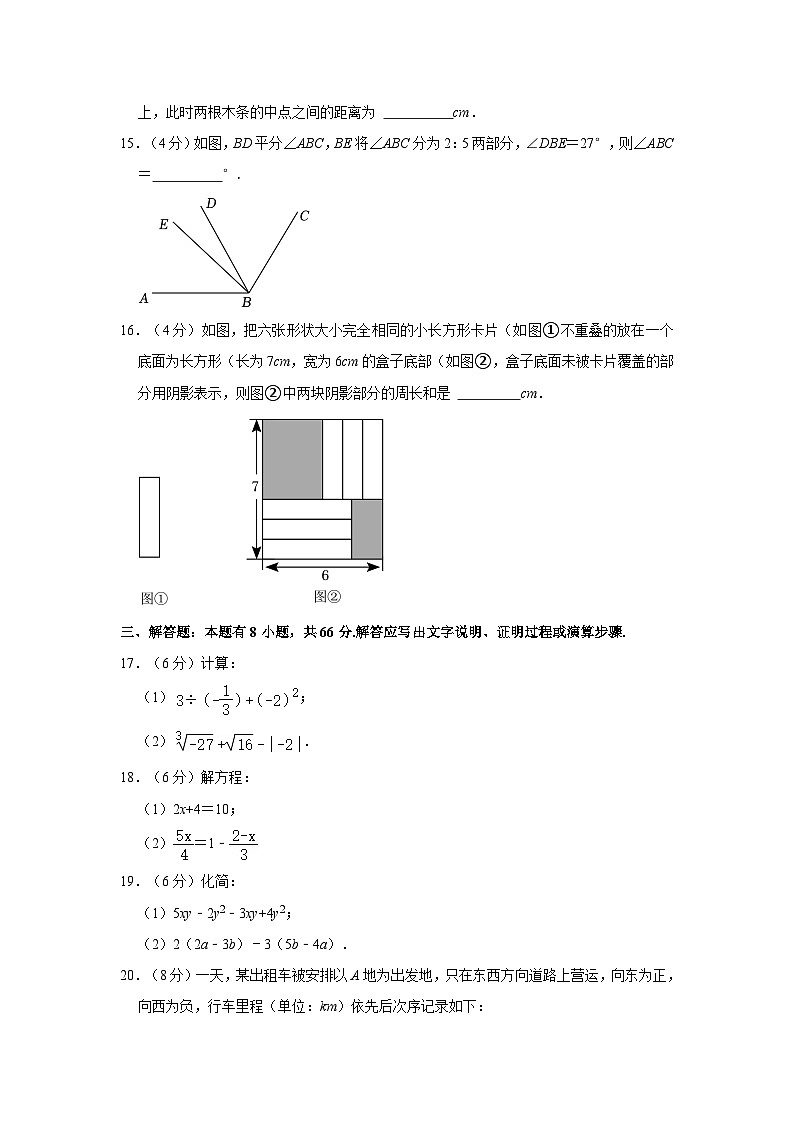
15．（4分）如图，BD平分∠ABC，BE将∠ABC分为2：5两部分，∠DBE＝27°，则∠ABC＝ °．
16．（4分）如图，把六张形状大小完全相同的小长方形卡片（如图①不重叠的放在一个底面为长方形（长为7cm，宽为6cm的盒子底部（如图②，盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是 cm．
三、解答题：本题有8小题，共66分.解答应写出文字说明、证明过程或演算步骤.
17．（6分）计算：
（1）；
（2）．
18．（6分）解方程：
（1）2x+4＝10；
（2）＝1﹣
19．（6分）化简：
（1）5xy﹣2y2﹣3xy+4y2；
（2）2（2a﹣3b）﹣3（5b﹣4a）．
20．（8分）一天，某出租车被安排以A地为出发地，只在东西方向道路上营运，向东为正，向西为负，行车里程（单位：km）依先后次序记录如下：
+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10．
假设该出租车每次乘客下车后，都在停车地等待下一个乘客，直到下一个乘客上车再出发．
（1）将最后一名乘客送到目的地，出租车在A地什么方向？距离A地多远？
（2）若出租车每千米车费是2.5元，司机当天的营业额是多少？
21．（8分）已知某正数的平方根分别是2a﹣7和a+4，b﹣12的立方根为﹣2．
（1）求a、b的值；
（2）求5a+b的算术平方根．
22．（10分）如图，将两块直角三角板AOB与COD的直角顶点O重合在一起，其中直角边OB在∠COD内部．
（1）如图，若∠AOC＝30°，求∠AOD和∠BOC的度数．
（2）若∠AOC＝α（0°＜α＜90°）．
①∠AOD和∠BOC有什么关系？请说明理由；
②当∠AOD＝4∠BOC时，求α的度数．
23．（10分）旅行社组织了甲、乙两个旅游团到游乐场游玩，两团总报名人数为120人，其中甲团人数不超过50人，游乐场规定一次性购票50人以上可享受团队票．门票价格如下：
旅行社经过计算后发现，如果甲、乙两团合并成一个团队购票可以比分开购票节约300元．
（1）求甲、乙两团的报名人数；
（2）当天到达游乐场后发现团队票价格作了临时调整，团队票A每张降价a元，团队票B每张降价2a元，同时乙团队因故缺席了30人，此时甲、乙两团合并成一个团队购票可以比分开购票节约225元，求a的值．
24．（12分）数轴上点A对应的数为a，点B对应的数为b，且多项式x3y﹣2xy+5的二次项系数为a，常数项为b．
（1）直接写出：a＝ ，b＝ ．
（2）若|x﹣a|+|x﹣b|＝9，利用绝对值的几何意义可知x＝ ．
（3）若点M从点A出发，以每秒1个单位长度的速度沿数轴向右移动；同时点N从点B出发，沿数轴以每秒2个单位长度的速度向左移动，到达A点后立即返回并向右继续移动，当M，N两点相距1个单位长度时，求M，N两点移动的时间．
参考答案与解析
一、选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项最符合题目要求.
1．（3分）2024的相反数是（ ）
A．2024B．﹣2024C．D．
【解答】解：2024的相反数是﹣2024，
故选：B．
2．（3分）记者从10月7日的杭州亚运会赛事总结新闻发布会上获悉，截至7日上午，杭州亚运会售票总数超过3050000张．将3050000这个数用科学记数法表示为（ ）
A．3.05×106B．30.5×105C．0.305×107D．3.05×107
【解答】解：3050000＝3.05×106．
故选：A．
3．（3分）估计的值在（ ）
A．6和7之间B．5和6之间C．4和5之间D．3和4之间
【解答】解：∵＜＜，
∴5＜＜6，
∴的值在5与6之间．
故选：B．
4．（3分）在下列各组单项式中，不是同类项的是（ ）
A．5x2y和﹣7x2yB．m2n和2mn2
C．﹣3和99D．﹣abc和9abc
【解答】解：A．5x2y和﹣7x2y所含字母相同，并且相同字母的指数也相同，是同类项，故本选项不合题意；
B．m2n和2mn2所含字母相同，但相同字母的指数不相同，故不是同类项，故本选项符合题意；
C．﹣3和99是同类项，故本选项不合题意；
D．﹣abc和9abc所含字母相同，并且相同字母的指数也相同，是同类项，故本选项不合题意．
故选：B．
5．（3分）实数abc在数轴上的对应点的位置如图所示，如果a+c＝0，那么下列结论正确的是（ ）
A．b＜0B．a＜﹣bC．ab＞0D．b﹣c＞0
【解答】解：∵a+c＝0，
∴a，c互为相反数，
∴原点在a，c中间，b＞0，
∴A选项不符合题意；
∵b在原点右侧，﹣b在原点左侧，
∵|c|＞|b|，
∴|a|＞|﹣b|，
∴a＜﹣b，B选项符合题意；
∵a＜0，b＞0，
∴ab＜0，C选项不符合题意；
b﹣c＜0，D选项不符合题意．
故选：B．
6．（3分）下列方程变形正确的是（ ）
A．方程3x﹣2＝2x+1，移项，得3x﹣2x＝﹣1+2
B．方程3﹣x＝2﹣5（x﹣1），去括号，得3﹣x＝2﹣5x﹣1
C．方程，未知数系数化为1，得t＝2
D．方程化成
【解答】解：A．3x﹣2＝2x+1，
移项，得3x﹣2x＝1+2，故本选项不符合题意；
B．3﹣x＝2﹣5（x﹣1），
去括号，得3﹣x＝2﹣5x+5，故本选项不符合题意；
C．t＝，
系数化成1，得t＝÷＝，故本选项不符合题意；
D．﹣＝1，
﹣＝1，故本选项符合题意；
故选：D．
7．（3分）如图，AB，CD交于点O，OE平分∠AOD，∠COB＝140°，则∠BOE的度数为（ ）
A．40°B．70°C．110°D．130°
【解答】解：∵OE平分∠AOD，
∴∠AOE＝∠AOD，
∵∠AOD＝∠BOC＝140°，
∴∠AOE＝70°，
∴∠BOE＝180°﹣∠AOE＝110°．
故选：C．
8．（3分）如图，大小两个正方形的边长分别是4和3，叠放在一起后两个阴影部分的面积分别为a，b（a＜b），则2a（a﹣1）﹣2（a2﹣b）的值为（ ）
A．2B．7C．14D．25
【解答】解：∵两个面积分别为4，3的图形叠放在一起，两个阴影部分的面积分别为a，b（a＜b），
∴b﹣a＝b+空白面积﹣（a+空白面积）＝大正六边形﹣小正六边形＝4﹣3＝1．
∴2a（a﹣1）﹣2（a2﹣b）＝2b﹣2a＝2（b﹣a）＝2，
故选：A．
9．（3分）若一个长方形的周长为42，将它的长减少3，宽增加2，恰好得到一个正方形，设这个正方形的边长为x，根据题意可列方程为（ ）
A．x+3+x﹣2＝21B．x﹣3+x+2＝21
C．x+3+x﹣2＝42D．x﹣3＝（21﹣x）+2
【解答】解：设长方形的长为x，则长方形的长为x+3，宽为x﹣2，
42÷2＝21．
由题意可得：x+3+x﹣2＝21．
故选：A．
10．（3分）下列说法正确的个数有（ ）
①一个四次多项式与一个五次多项式的和一定是一个五次整式．
②三条直线相交，有三个交点．
③连接两点间的线段，叫做这两点的距离．
④若有理数a和b互为相反数，则一定有a＝﹣b．
⑤若线段AB＝BC，则点B是线段AC的中点．
A．1个B．2个C．3个D．4个
【解答】解：①一个四次多项式与一个五次多项式的和一定是一个五次整式，不符合题意；
②三条直线相交，有一个或三个交点，符合题意；
③连接两点间的线段的长度，叫做这两点的距离，不符合题意；
④连接两点间的线段的长度，叫做这两点的距离，符合题意；
⑤若有理数a和b互为相反数，则一定有a＝﹣b，不符合题意；
⑥点B在线段AC上，如果AB＝BC，则点B是线段AC的中点，所以原说法符合题意．
故选：C．
二、填空题：本题有6个小题，每小题4分，共24分.
11．（4分）用四舍五入法把数1.3579精确到百分位，所得的近似数是 1.36 ．
【解答】解：1.3579≈1.36（精确到百分位）．
故答案为：1.36．
12．（4分）在数轴上，若A点表示﹣3，在A点左侧到点A距离等于2的点所表示的数是 ﹣5 ．
【解答】解：∵A点表示﹣3．
∴在A点左侧到点A距离等于2的点所表示的数是﹣3﹣2＝﹣5．
故答案为：﹣5．
13．（4分）如果x＝1是关于x的方程x﹣2m＝9的解，则m的值为 ﹣4 ．
【解答】解：∵x＝1是关于x的方程x﹣2m＝9的解，
∴1﹣2m＝9，
解得：m＝﹣4，
故答案为：﹣4．
14．（4分）两根木条，一根长10cm，另一根长8cm，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为 1或9 cm．
【解答】解：设AC＝8cm，AB＝10cm，根据题意，
①如图1，
∵点E是AC的中点，点D是AB的中点，
∴，，
∴ED＝AE+AD＝4+5＝9（cm）；
②如图2，
∵点E是AC的中点，点D是AB的中点，
∴，，
∴ED＝AD﹣AE＝5﹣4＝1（cm）．
综上所述，两根木条的中点之间的距离为1cm或9cm．
故答案为：1或9．
15．（4分）如图，BD平分∠ABC，BE将∠ABC分为2：5两部分，∠DBE＝27°，则∠ABC＝ 126 °．
【解答】解：设∠ABC＝α，则∠ABD＝，∠ABE＝α，
∵∠DBE＝∠ABD﹣∠ABE，
∴﹣α＝27°，
解得：α＝126°，
故答案为：126．
16．（4分）如图，把六张形状大小完全相同的小长方形卡片（如图①不重叠的放在一个底面为长方形（长为7cm，宽为6cm的盒子底部（如图②，盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是 24 cm．
【解答】解：设小长方形卡片的长为a cm，宽为b cm，
图②中两块阴影部分的周长和是：2a+（6﹣3b）×2+3b×2+（6﹣a）×2
＝2a+12﹣6b+6b+12﹣2a
＝24（cm），
故答案为：24．
三、解答题：本题有8小题，共66分.解答应写出文字说明、证明过程或演算步骤.
17．（6分）计算：
（1）；
（2）．
【解答】解：（1）
＝3×（﹣3）+4
＝﹣9+4
＝﹣5．
（2）
＝﹣3+4﹣2
＝﹣1．
18．（6分）解方程：
（1）2x+4＝10；
（2）＝1﹣
【解答】解：（1）移项得：2x＝10﹣4，
合并同类项得：2x＝6，
系数化为1得：x＝3，
（2）去分母得：15x＝12﹣4（2﹣x），
去括号得：15x＝12﹣8+4x，
移项得：15x﹣4x＝12﹣8，
合并同类项得：11x＝4，
系数化为1得：x＝．
19．（6分）化简：
（1）5xy﹣2y2﹣3xy+4y2；
（2）2（2a﹣3b）﹣3（5b﹣4a）．
【解答】解：（1）原式＝（5﹣3）xy+（﹣2+4）y2
＝2xy+2y2；
（2）原式＝4a﹣6b﹣15b+12a
＝（4+12）a﹣（6+15）b
＝16a﹣21b．
20．（8分）一天，某出租车被安排以A地为出发地，只在东西方向道路上营运，向东为正，向西为负，行车里程（单位：km）依先后次序记录如下：
+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10．
假设该出租车每次乘客下车后，都在停车地等待下一个乘客，直到下一个乘客上车再出发．
（1）将最后一名乘客送到目的地，出租车在A地什么方向？距离A地多远？
（2）若出租车每千米车费是2.5元，司机当天的营业额是多少？
【解答】解：（1）（+9）+（﹣3）+（﹣5）+（+4）+（﹣8）+（+6）+（﹣7）+（﹣6）+（﹣4）+（+10）＝﹣4（千米），
答：将最后一名乘客送到目的地，出租车在A地西边，距离A地4千米．
（2）|+9|+|﹣3|+|﹣5|+|+4|+|﹣8|+|+6|+|﹣7|+|﹣6|+|﹣4|+|+10|＝62（千米），
62×2.5＝155（元），
答：司机当天的营业额是155元．
21．（8分）已知某正数的平方根分别是2a﹣7和a+4，b﹣12的立方根为﹣2．
（1）求a、b的值；
（2）求5a+b的算术平方根．
【解答】解：（1）∵某正数的平方根是2a﹣7和a+4，
∴2a﹣7+a+4＝0，
解得：a＝1，
∵b﹣12的立方根为﹣2，
∴b﹣12＝（﹣2）3，
∴b﹣12＝﹣8，
解得：b＝4，
∴a＝1，b＝4；
（2）∵5a+b＝5+4＝9，
∴5a+b的算术平方根为3．
22．（10分）如图，将两块直角三角板AOB与COD的直角顶点O重合在一起，其中直角边OB在∠COD内部．
（1）如图，若∠AOC＝30°，求∠AOD和∠BOC的度数．
（2）若∠AOC＝α（0°＜α＜90°）．
①∠AOD和∠BOC有什么关系？请说明理由；
②当∠AOD＝4∠BOC时，求α的度数．
【解答】解：（1）∵∠AOB＝∠COD＝90°，∠AOC＝30°，
∴∠AOD＝∠AOC+∠COD＝30°+90°＝120°；∠BOC＝∠AOB﹣∠AOC＝90°﹣30°＝60°；
（2）①∠AOD+∠BOC＝180°，理由如下：
∵∠AOB＝∠COD＝90°，∠AOC＝α（0°＜α＜90°），
∴∠AOD＝∠AOC+∠COD＝α+90°，∠BOC＝∠AOB﹣∠AOC＝90°﹣α，
∴∠AOD+∠BOC＝α+90°+90°﹣α＝180°；
②由①可知：∠AOD+∠BOC＝180°，
又∵∠AOD＝4∠BOC，
∴4∠BOC+∠BOC＝180°，
∴∠BOC＝36°，
∴∠AOC＝∠AOB﹣∠BOC＝90°﹣36°＝54°．
即α＝54°．
23．（10分）旅行社组织了甲、乙两个旅游团到游乐场游玩，两团总报名人数为120人，其中甲团人数不超过50人，游乐场规定一次性购票50人以上可享受团队票．门票价格如下：
旅行社经过计算后发现，如果甲、乙两团合并成一个团队购票可以比分开购票节约300元．
（1）求甲、乙两团的报名人数；
（2）当天到达游乐场后发现团队票价格作了临时调整，团队票A每张降价a元，团队票B每张降价2a元，同时乙团队因故缺席了30人，此时甲、乙两团合并成一个团队购票可以比分开购票节约225元，求a的值．
【解答】解：（1）设乙团x人，则甲团（120﹣x）人，
①当70≤x≤100时，两团队门票款之和为：70x+80（120﹣x）﹣60×120＝300，
解得：x＝210（舍去）；
②当x＞100时，两团队门票款之和为：60x+80（120﹣x）﹣60×120＝300，
解得：x＝105，
答：甲团15人，乙团105人；
（2）由题意得：15×80+75×（70﹣a）＝90×（70﹣a）+225，
解得：a＝5．
24．（12分）数轴上点A对应的数为a，点B对应的数为b，且多项式x3y﹣2xy+5的二次项系数为a，常数项为b．
（1）直接写出：a＝ ﹣2 ，b＝ 5 ．
（2）若|x﹣a|+|x﹣b|＝9，利用绝对值的几何意义可知x＝ ﹣3或6 ．
（3）若点M从点A出发，以每秒1个单位长度的速度沿数轴向右移动；同时点N从点B出发，沿数轴以每秒2个单位长度的速度向左移动，到达A点后立即返回并向右继续移动，当M，N两点相距1个单位长度时，求M，N两点移动的时间．
【解答】解：（1）∵多项式x3y﹣2xy+5的二次项系数为a，常数项为b，
∴a＝﹣2，b＝5，
故答案为：﹣2，5；
（2）∵|x﹣a|+|x﹣b|＝9，
∴表示x的点到表示﹣2和5点的距离之和为9，
当x＜﹣2时，得：﹣x﹣2+5﹣x＝9，
解得：x＝﹣3；
当x＞5时，得：x+2+x﹣5＝9，
解得：x＝6，
∴a＝﹣3或6，
故答案为：﹣3或6；
（3）设经过t秒后，M、N两点相距1个单位长度，
由运动知，AM＝t，BN＝2t，
（法一）
①当点N到达点A之前时，
Ⅰ、当M，N相遇前，M、N两点相距1个单位长度，
t+1+2t＝5+2，
所以，t＝2秒．
Ⅱ、当M，N相遇后，M、N两点相距1个单位长度，
t+2t﹣1＝5+2，
所以，t＝秒．
②当点N到达点A之后时，
Ⅰ、当N未追上M时，M、N两点相距1个单位长度，
t﹣[2t﹣（5+2）]＝1，
所以，t＝6秒；
Ⅱ、当N追上M后时，M、N两点相距1个单位长度，
[2t﹣（5+2）]﹣t＝1，
所以，t＝8秒；
即：经过2秒或秒或6秒或8秒后，M、N两点相距1个单位长度．
（法二）当点N到达点A之前时，|（﹣2+t）﹣（5﹣2t）|＝1，
所以t1＝2，t2＝，
当点N到达点A之后时，|（﹣2+t）﹣（﹣2+2t﹣7）|＝1，
所以t3＝6，t4＝8，
即：当M，N两点相距1个单位长度时，M，N两点移动的时间为2秒或秒或6秒或8秒．门票类别
散客票
团队票A
团队票B
购票要求
超过50人但不超过100人
超过100人
票价（元/人）
80元/人
70元/人
60元/人
门票类别
散客票
团队票A
团队票B
购票要求
超过50人但不超过100人
超过100人
票价（元/人）
80元/人
70元/人
60元/人