第1-2单元阶段月考B卷-2023-2024学年五年级下册数学易错点月考卷（人教版）

这是一份第1-2单元阶段月考B卷-2023-2024学年五年级下册数学易错点月考卷（人教版），共13页。试卷主要包含了请将答案正确填写在答题卡上等内容，欢迎下载使用。

2023-2024学年五年级下册数学易错点检测卷（人教版）
学校:__________姓名：___________班级：___________考号：___________
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
一、选择题（共12分）
1．两个奇数的和一定是（ ）。
A．奇数B．偶数C．合数D．质数
2．用4个同样大小的正方体搭成的几何体，从正面看是，从左面看是，从上面看是，符合要求的几何体是（ ）。
A． B． C． D．
3．用4、2、6三个数字组成的没有重复数字的三位数中，3的倍数有（ ）个。
A．3B．4C．5D．6
4．一个数既是30的因数，又是5的倍数，这个数不可能是（ ）。
A．5B．10C．25D．30
5．下面各数中，既不是2的倍数，又不是5的倍数的是（ ）。
A．92B．110C．471D．866
6．某小学有312□名学生，已知学生的人数既是2的倍数，又是3的倍数，□里的数是（ ）。
A．0B．2C．5D．8
二、填空题（共23分）
7．自然数中，既是质数又是偶数的数是( )，既是奇数又是合数的最小两位数是( )．
8．91至少减去( )就是3的倍数，94至少加上( )就是5的倍数。
9．3826至少减去( )就是3的倍数，2303至少加上( )就是5的倍数。
10．奇数＋奇数＝( )，奇数－奇数＝( )，奇数×奇数＝( )。
11．一个立体图形，从正面看到的形状是，从左面看到的形状是，搭这个立体图形至少要( )个小正方体，最多要( )个小正方体。
12．35÷7=5其中( )是( )和( )的倍数，( )是( )的因数。
13．如果734□是3的倍数，则□里最小能填( )，最大能填( )。
14．在14，3，2.4，8，144这四个数中，( )是( )的倍数，其中( )是质数。
15．五（1）班进行体操表演。若每行10人，则少2人；若每行8人，则正好排整行。已知这个班的学生人数在40到50之间，这个班有学生( )人。
16．在1、4、6、7、47、33和91这几个数中，一共有( )个质数。
三、判断题（共7分）
17．能被2整除的数都是偶数，不能被2整除的数都是奇数。( )
18．一个数的因数一定比它的倍数小。( )
19．因为4×5＝20，所以20是倍数，4是因数。( )
20．一个长方形的周长是24厘米，它的长和宽都是质数，那么这个长方形的面积是11平方厘米。( )
21．因为27÷3＝9，所以27是倍数，3是因数。( )
22．六年级150名同学排成4行。如果前3行每行的人数都是奇数，那么第4行的人数一定是奇数。( )
23．有三张卡片，在它们的上面各写一个数字2、3、7，从中至少取出一张组成一个数，在组成的所有数中，有6个是质数。( )
四、计算题（共15分）
24．直接写得数。 （共5分）
25×0.2＝ 0×5.8＝ 1.25×4＝ 4.05×4＝ 0.6＋4.4×2＝
6÷100＝ 2.2÷0.1＝ 2.4÷0.6＝ 0.6÷0.02＝ 5×0.4÷5×0.4＝
25．用简便方法计算，写出主要计算过程．（共10分）
（1）2.12×2.7+7.88×2.7 （2）1.25×0.25×3.2 （3）24×10.2
（4）5.7×99+5.7 （5）21.36÷0.8﹣12.9．
五、解答题（共43分）
26．4个棱长为30厘米的正方体想箱子放在墙角处．
（1）分别画出从正面、右面、上面看到的图形．
（2）共有________个面露在外面，露在外面的面积是________平方厘米．
27．一个五位数27a8b，既能被3整除，又能被5整除，a与b可为哪些数字？
28．如果两个质数正好相差2，我们就把它们称为“孪生质数”（例如，3和5是一对孪生质数，5和7又是一对）。在自然数1～100中，孪生质数还有哪几对？请写出来。
文具店运来45块橡皮擦，如果每2块装一盒，能正好装完吗？如果每3块装一盒，能正好装完吗？如果每5块装一盒，能正好装完吗？请说明理由。


30．由8个不同的数字组成的八位数中，能被396整除的数最大是多少？最小是多少？
31．筐里有30个苹果，将它们全部取出来，分成若干堆（堆数大于1，而小于30），使每堆中苹果的个数相等，有几种分法？
32．三位同学商定暑假去体育馆训练踢足球，小峰说：“我每4天去一次。”小亮说：“我每8天去一次。”小勇说：“我每6天去一次。”如果三人7月10日同时去体育馆踢球，那么至少再过多少天，他们中有两人会在体育馆相遇？
33．张乐到文具店买了3本同样的笔记本，单价是整数元，售货员阿姨说应付23元。售货员阿姨算得对不对？为什么？
参考答案：
1．B
【分析】由和的奇偶性可知，偶数＋偶数＝偶数，奇数＋奇数＝偶数，奇数＋偶数＝奇数，据此解答。
【详解】两个奇数的和一定是偶数，假设这两个奇数为3和17，3＋17＝20，20是偶数。
故答案为：B
两个加数的奇偶性相同时，和一定为偶数；两个加数的奇偶性不相同时，和一定是奇数。
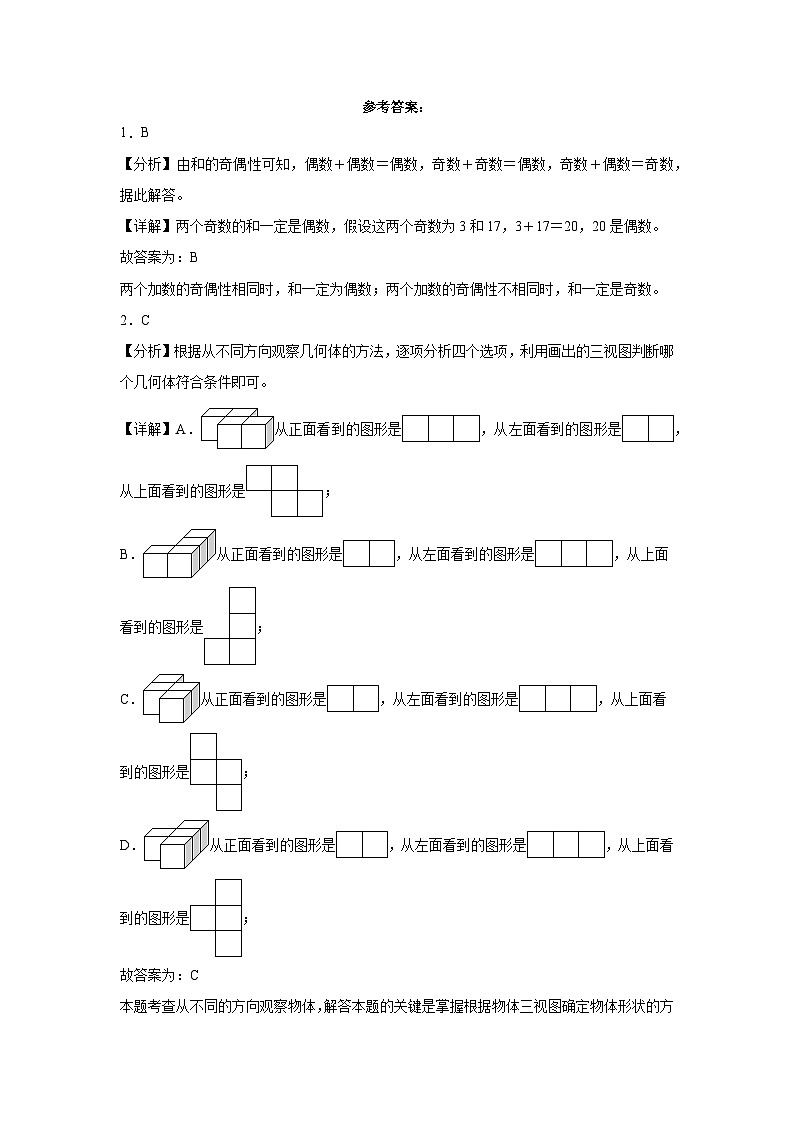
2．C
【分析】根据从不同方向观察几何体的方法，逐项分析四个选项，利用画出的三视图判断哪个几何体符合条件即可。
【详解】A．从正面看到的图形是，从左面看到的图形是，从上面看到的图形是；
B．从正面看到的图形是，从左面看到的图形是，从上面看到的图形是；
C．从正面看到的图形是，从左面看到的图形是，从上面看到的图形是；
D．从正面看到的图形是，从左面看到的图形是，从上面看到的图形是；
故答案为：C
本题考查从不同的方向观察物体，解答本题的关键是掌握根据物体三视图确定物体形状的方法。
3．D
【分析】用4、2、6三个数字组成的没有重复数字的三位数有：426，462，246，264，624，642，共6个，然后根据3的倍数特征：各个数位上数字之和是3的倍数，这个数就是3的倍数。据此判断即可。
【详解】由分析可知：
4＋2＋6＝12，12是3的倍数，所以4、2、6这三个数字组成的没有重复数字的6个三位数都是3的倍数。
故答案为：D
本题考查3的倍数，明确3的倍数特征是解题的关键。
4．C
【分析】求30的因数时，把自然数从1开始乘，只需要乘得的积是30的两个乘数都是它的因数。
求5的倍数，用5分别乘自然数1、2、3、4、5…，所得积就是5的倍数；
分别写出30以内30的因数和5的倍数，即可得出答案。
【详解】30的因数有：1、2、3、5、6、10、15、30；
5的倍数有：5、10、15、20、25、30……
选项中，A、B、D都同时是30的因数和5的倍数；只有C不是30的因数；
故答案为：C
本题主要考查求一个数的因数和倍数的方法，注意一个数的倍数是无限的。
5．C
【分析】2的倍数的数的特征是：个位上是0、2、4、6、8的数；5的倍数的数的特征是：个位上是0或5的数都是5的倍数；由此解答。
【详解】A．92是2的倍数，但不是5的倍数；不符合题意；
B．110既是2的倍数，也是5的倍数；不符合题意；
C．471既不是2的倍数，又不是5的倍数；符合题意；
D．866是2的倍数，但不是5的倍数；不符合题意；
故答案为：C
熟练掌握2、5倍数的特征是解答本题的关键。
6．A
【分析】同时是2和3的倍数特征：个位上是0、2、4、6或8，且各个数位上的数字和是3的倍数。据此解答。
【详解】A．3＋1＋2＋0＝6
6是3的倍数，所以3120既是2的倍数，又是3的倍数。
B．3＋1＋2＋2＝8
8不是3的倍数，所以3122不符合题意；
C．3125不是2的倍数，所以3125不符合题意；
D．3＋1＋2＋8＝14
14不是3的倍数，所以3128不符合题意。
故答案为：A
熟练掌握2、3的倍数的特征是解决此题的关键。
7． 2 15
【详解】略
8． 1 1
【分析】一个数的各个数位上的数的和能被3整除，这个数就能被3整除；个位上是0或者5的数，都能被5整除。据此解答。
【详解】9＋1＝10
10－9＝1
因为9能被3整除，所以至少应减去1。
5－4＝1
94的个位上是4，根据5的倍数的特征，至少加上1。
所以，91至少减去1就是3的倍数，94至少加上1就是5的倍数。
此题考查的目的是理解掌握3、5的倍数的特征及应用。
9． 1 2
【分析】3的倍数特点是各个数位上的数字相加和是3的倍数，3826各个数位上的数字相加和是19，因为18是3的6倍，所以19减去1就是3的倍数，因此3826至少减去1就是3的倍数；5的倍数特点是个位上的数字是0或5，2303各位上是3，所以至少加上2就是5的倍数。
【详解】3＋8＋2＋6
＝11＋8
＝19
19－1＝18
18÷3＝6
所以3826至少减去1就是3的倍数；
5－3＝2
2303＋2＝2305
2305÷5＝461
所以2303至少加上2就是5的倍数
考查3和5的倍数特点，重点是能够清楚的知道3的倍数特点是各个数位上的数字相加和是3的倍数。
10． 偶数 偶数 奇数
【分析】根据奇数和偶数的运算性质：①奇数±奇数＝偶数；②奇数×奇数＝奇数；据此解答。
【详解】根据分析得，奇数＋奇数＝偶数；
奇数－奇数＝偶数；
奇数×奇数＝奇数。
此题的解题关键是理解掌握奇数和偶数的运算性质。
11． 4 7
【分析】如图，是搭这个立体图形至少需要的小正方体；如图，是最多需要的小正方体，据此填空。
【详解】一个立体图形，从正面看到的形状是，从左面看到的形状是，搭这个立体图形至少要4个小正方体，最多要7个小正方体。
本题考查了从不同方向观察几何体，要有一定的空间想象能力，或画出示意图。
12． 35 5 7 5和7 35
【解析】略
13． 1 7
【分析】3的倍数特征：各个数位上的数字相加，和要能被3整除；据此解答。
【详解】7＋3＋4＝14，不是3的倍数；
14＋1＝15，是3的倍数；
14＋4＝18，是3的倍数；
14＋7＝21，是3的倍数；
如果734□是3的倍数，则□里最小能填1，最大能填7。
掌握3的倍数特征是解题的关键。
14． 144 3 3
【分析】（1）在整数除法中，如果商是整数而没有余数，我们就说被除数是除数和商的倍数，除数和商是被除数的因数；
（2）一个数，如果只有1和它本身两个因数，那么这样的数叫做质数；据此解答。
【详解】（1）144÷3＝48，144÷8＝18，则144是3的倍数，144是8的倍数；
（2）3的因数只有1和3，所以3是质数。
掌握因数、倍数、质数的意义是解答题目的关键。
15．48
【分析】每行8人刚好排整行，总人数是8的倍数，每行10人，则少2人，总人数加上2应该是10的倍数；在40到50之间的8的倍数有40和48，40＋2＝42不是10的倍数排除，48＋2＝50，刚好是10的倍数，符合题意。
【详解】根据分析可知，这个班的人数有48人。
此题考查一个数的倍数的求法，解决问题的关键在于明确倍数的取值范围。
16．2
【分析】一个自然数，如果只有1和它本身两个因数，这样的数叫做质数；一个自然数，如果除了1和它本身还有别的因数，这样的数叫做合数；由此解答。
【详解】1的因数只有1，1既不是质数，也不是合数；
4的因数有1、2、4，4是合数；
6的因数有1、2、3、6，6是合数；
7的因数只有1、7，7是质数；
47的因数只有1、47，47是质数；
33的因数有1、3、11、33，33是合数；
91的因数有1、7、13、91，91是合数；
在1、4、6、7、47、33和91这几个数中，一共有2个质数。
掌握质数、合数的概念及意义是解题的关键。
17．√
【详解】根据奇数和偶数的分类标准，能被2整除的数都是偶数，不能被2整除的数都是奇数，说法正确。
故答案为：√
18．×
【分析】一个数因数的个数是有限的，最小的因数是1，最大的因数是这个数本身，一个数倍数的个数是无限的，最小的倍数是这个数本身，没有最大的倍数，据此解答。
【详解】分析可知，一个数的最大因数等于这个数的最小倍数，都是这个数本身，如：4是4的因数，4也是4的倍数。
故答案为：×
熟记一个数的最大因数等于这个数的最小倍数是解答题目的关键。
19．×
【分析】因数与倍数都是表达两个数之间的关系，所以一定要说清楚谁是谁的因数，谁是谁的倍数，据此解答即可。
【详解】4×5＝20，4和5是20的因数，20是4和5的倍数，原题说法错误。
故答案为：×
一定要明确因数与倍数都表达两个数之间的关系，是相互的。
20．×
【分析】根据长方形的周长＝（长＋宽）×2可知，长＋宽＝周长÷2，即12厘米；然后考虑哪两个数相加的和是12厘米，且这两个数都是质数，即可找出长方形的长与宽；再根据长方形的面积＝长×宽，求出这个长方形的面积，据此判断。
【详解】24÷2＝12（厘米）
12＝11＋1＝10＋2＝9＋3＝8＋4＝7＋5
其中7和5是质数，所以这个长方形的长是7厘米，宽是5厘米；
长方形的面积：7×5＝35（平方厘米）
原题说法错误。
故答案为：×
掌握质数的定义、长方形的周长、面积公式是解题的关键。
21．×
【分析】因数和倍数是相互依存的，离开了因数也就无所谓倍数，离开了倍数也就无所谓因数，应当说哪个数是哪个数的因数，哪个数是哪个数的倍数，本题应当说27是3和9的倍数，3和9是27的因数。
【详解】因为27÷3＝9
所以27是3和9的倍数，3和9是27的因数。
原题说法错误。
故答案为：×
本题是考查因数与倍数的意义。要记住，因数和倍数是相互依存的。
22．√
【分析】4行同学的人数和是150，150是一个偶数，根据“奇数＋奇数＝偶数”“偶数＋偶数＝偶数”列式判断第4行的人数是奇数还是偶数，据此解答。
【详解】第1行的人数＋第2行的人数＋第3行的人数＋第4行的人数＝150人
奇数＋奇数＋第3行的人数＋第4行的人数＝偶数
（奇数＋奇数）＋（第3行的人数＋第4行的人数）＝偶数
偶数＋（第3行的人数＋第4行的人数）＝偶数
则第3行的人数＋第4行的人数＝偶数，因为第3行的人数是奇数，所以第4行的人数也是奇数。
故答案为：√
本题主要考查和差的奇偶性，掌握奇数、偶数的运算性质是解答题目的关键。
23．√
【分析】将所有组成的数写出来，数一数有几个质数即可。
【详解】从2、3、7中至少取出一张组成一个数，组成的数有：2、3、7、23、27、32、37、72、73、237、273、327、372、723、732，其中质数有：2、3、7、23、37、73，共6个，所以原题说法正确。
本题考查了搭配问题及质数，除了1和它本身以外不再有其他因数，这样的数叫质数。
24．5；0；5；16.2；9.4
0.06；22；4；30；0.16
【分析】根据小数乘除法的计算方法，直接进行口算即可。
【详解】25×0.2＝5 0×5.8＝0 1.25×4＝5 4.05×4＝16.2 0.6＋4.4×2＝0.6＋8.8＝9.4
6÷100＝0.06 2.2÷0.1＝22 2.4÷0.6＝4 0.6÷0.02＝30 5×0.4÷5×0.4＝5÷5×0.4×0.4＝0.16
本题考查了小数乘除法的口算，计算时要认真。
25．27；1；244.8；570；13.8
【详解】试题分析：（1）根据乘法分配律，计算即可；
（2）3.2=0.8×4，然后根据乘法交换律和结合律，计算即可；
（3）10.2=10+0.2，然后根据乘法分配律；
（4）根据乘法分配律，计算即可；
（5）首先计算除法，然后计算减法；即可得解．
解：（1）2.12×2.7+7.88×2.7
=（2.12+7.88）×2.7
=10×2.7
=27
（2）1.25×0.25×3.2
=1.25×0.25×（0.8×4）
=（1.25×0.8）×（0.25×4）
=1×1
=1
（3）24×10.2
=24×（10+0.2）
=24×10+24×0.2
=240+4.8
=244.8
（4）5.7×99+5.7
=5.7×（99+1）
=5.7×100
=570
（5）21.36÷0.8﹣12.9
=26.7﹣12.9
=13.8
【点评】完成本题要注意分析式中数据，运用合适的简便方法计算．
26．（1）
（2）9；8100
【分析】（1）从正面观察，可以看见两层，下面一层3个正方形一排，上面一层1个正方形居左；从右面看，可以看到两个正方形一列；从上面看，可以看到3个正方形一行，据此作图即可；
（2）从正面看，露在外面的面是4个正方形面，从上面看，露在外面的面是3个正方形面，从右面看，露在外面的面是2个正方形面，用加法可以求出露在外面的面一共有几个；要求露在外面的面积，用一个面的面积×露在外面的面数=露在外面的面积之和，据此列式解答.
【详解】（1）根据分析，作图如下：
.
（2）4+3+2=9（个）；
30×30×9
=900×9
=8100（平方厘米）.
27．b＝0，a为1、4、7
b＝5，a为2、5、8。
【分析】能同时被3和5整除的数的特征：个位上必须是0或5，且各位上的数字之和是3的倍数，据此解答。
【详解】由分析得，
当b＝0，2＋7＋8＋0＝17，还需加上1、4、7，才是3的倍数，所以a为1、4、7；
当b＝5，2＋7＋8＋5＝22，还需加上2、5、8，才是3的倍数，所以a为2、5、8。
所以，当b＝0，a为1、4、7
b＝5，a为2、5、8。
此题考查的是整除的性质的应用，解答此题关键是掌握同时被3和5整除的数的特征。
28．11和13 ；17和19； 29和31 ； 41和43；59和61；71和73
【分析】写出100以内所有质数，把相差2的找出来即可。
【详解】100以内的质数有：2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97，正好相差2的还有：11和13；17和19；29和31；41和43；59和61；71和73
本题考查了质数，只有1和它本身两个因数的数叫质数。
29．不能；能；能
【分析】45的个位是5，所以它不是2的倍数；4＋5＝9，所以45是3的倍数；45的个位是5，所以45是5的倍数。据此再结合题意，解题即可。
【详解】答：每2块装一盒，不能正好装完；
每3块装一盒，能正好装完；
每5块装一盒，能正好装完。
因为45是3和5的倍数，不是2的倍数。
本题考查了2、5、3的倍数特征。个位上是0、2、4、6、8的数，是2的倍数；个位上是0或5的数，是5的倍数；各位上数的和是3的倍数的数，是3的倍数。
30．最大是97860312，最小是12376980．
【详解】试题分析：能被396整除，就是既要能被9整除，又要能被4、11整除；0、1、2、3、4、5、6、7、8、9，10个不同数字，和为45，要去掉两个，剩下数字的和仍然是9的倍数，可以去掉4和5，剩下0、1、2、3、6、7、8、9，八位数能被4整除的充分必要条件是末两位能被4整除，又因为是11的倍数的特征是：奇位上的数字之和与偶位上数字之差能被11整除，所以这个八位数最小是12376980，最大是97860312，据此解答即可．
解：能被396整除，就是既要能被9整除，又要能被4、11整除；
因为0+1+2+3+4+5+6+7+8+9=45，要去掉两个，剩下数字的和仍然是9的倍数，
可以去掉4和5，剩下0、1、2、3、6、7、8、9，
因为八位数能被4整除的充分必要条件是末两位能被4整除，
八位数是11的倍数的特征是：奇位上的数字之和与偶位上数字之差能被11整除，
所以这个八位数最大是97860312，最小是12376980．
答：这个八位数最大是97860312，最小是12376980．
点评：此题主要考查了最大与最小问题的应用，解答此题的关键是熟练掌握是4、9、11的倍数的数的特征．
31．6种
【分析】找出30的因数就可以，但是要把1和30去掉，因为堆数大于1，而小于30。
【详解】30＝1×30＝2×15＝3×10＝5×6
所以每堆2个苹果，分15堆；
每堆3个苹果，分10堆；
每堆5个苹果，分6堆；
每堆6个苹果，分5堆；
每堆10个苹果，分3堆；
每堆15个苹果，分2堆。
答：有6种分法。
考查一个数的因数是多少。
32．8天
【分析】找出这三个数中任意两个数的最小公倍数，就是至少再过多少天才能有两个人相遇。
【详解】4和8的最小公倍数是：8；
4和6的最小公倍数是：12；
8和6的最小公倍数是：24；
8＜12＜24
答：至少再过8天有两人相遇在体育馆。
考查最小公倍数的相关应用。
33．不对；理由见详解
【分析】单价×数量＝总价，买了3本同样的笔记本，总钱数一定是3的倍数。3的倍数的特征：一个数各个数位上的数字的和是3的倍数，这个数就是3的倍数，据此分析。
【详解】笔记本单价×3＝总钱数，总钱数是3的倍数。
2＋3＝5
23不是3的倍数。
答：算得不对，23不是3的倍数。
关键是掌握3的倍数的特征。