




专题68 分段函数在生活实际中的应用(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用)
展开【例1】.某公司专销产品A,第一批产品A上市40天内全部售完、该公司对第一批产品A上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图(1)中的折线表示的是市场日销售量与上市时间的关系;图(2)中的折线表示的是每件产品A的销售利润与上市时间的关系.
(1)写出第一批产品A的市场日销售量y与上市时间t的关系式;
(2)写出每件产品A的销售利润z与上市时间t的关系式;
(3)第一批产品A上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?
解:(1)由图1可得,
当0≤t≤30时,设市场的日销售量y=kt,
∵点(30,60)在图象上,∴60=30k,
∴k=2,即y=2t;
当30<t≤40时,设市场的日销售量y=k1t+b,
∵点(30,60)和(40,0)在图象上,
∴
解得k1=﹣6,b=240.
∴y=﹣6t+240.
故y=;
(2)由图②可得:
当0≤t≤20时,每件产品的日销售利润为z=3t;
当20<t≤40时,每件产品的日销售利润为z=60;
故z=;
(3)①当0≤t≤20时,
w=3t•2t=6t2.
t=20时,w的最大值为2400(万元);
②当20<t≤30时,
w=2t•60=120t.
t=30时,w的最大值为3600(万元);
③当30<t≤40时,
w=60(﹣6t+240)
=﹣360t+14400
∵k=﹣360<0,
∴w随t的增大而减小.
∴w<﹣360×30+14400
即w<3600(万元)
∴第30天取最大利润3600万元.
变式训练
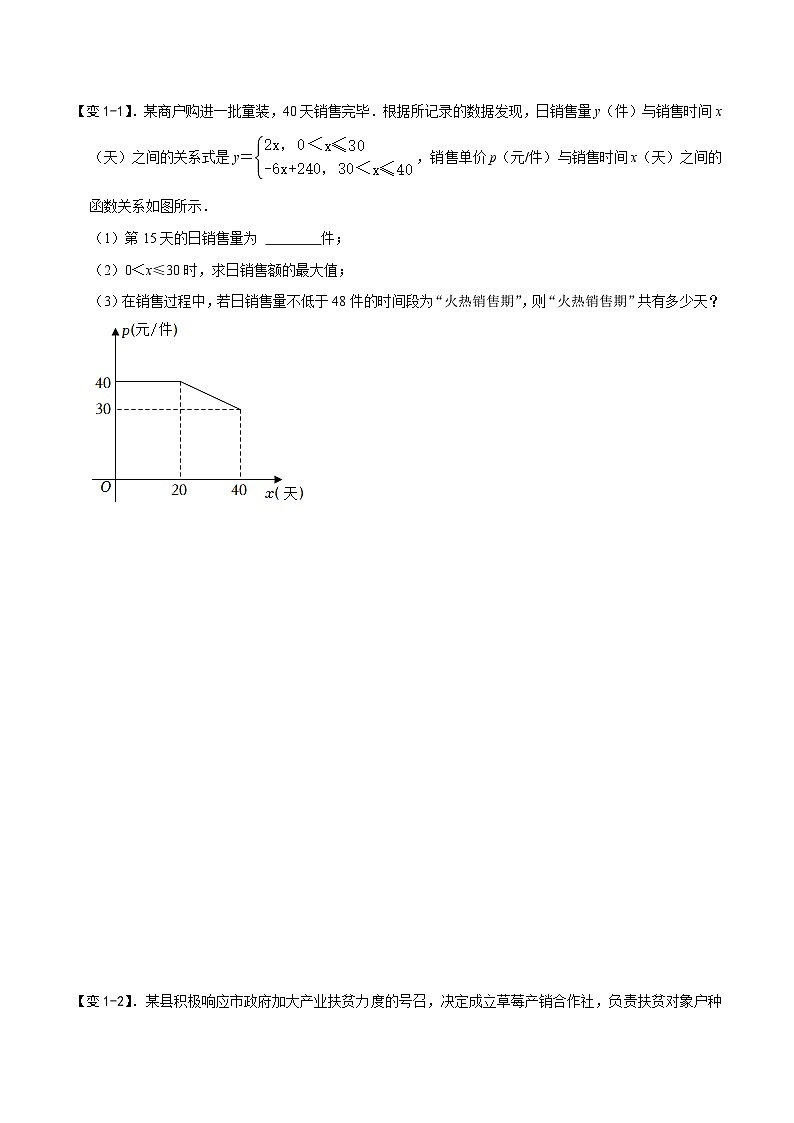
【变1-1】.某商户购进一批童装,40天销售完毕.根据所记录的数据发现,日销售量y(件)与销售时间x(天)之间的关系式是y=,销售单价p(元/件)与销售时间x(天)之间的函数关系如图所示.
(1)第15天的日销售量为 30 件;
(2)0<x≤30时,求日销售额的最大值;
(3)在销售过程中,若日销售量不低于48件的时间段为“火热销售期”,则“火热销售期”共有多少天?
解:(1)∵日销售量y(件)与销售时间x(天)之间的关系式是y=,
∴第15天的销售量为2×15=30件,
故答案为:30;
(2)由销售单价p(元/件)与销售时间x(天)之间的函数图象得:
p=,
①当0<x≤20时,
日销售额=40×2x=80x,
∵80>0,
∴日销售额随x的增大而增大,
∴当x=20时,日销售额最大,最大值为80×20=1600(元);
②当20<x≤30时,
日销售额=(50﹣x)×2x=﹣x2+100x=﹣(x﹣50)2+2500,
∵﹣1<0,
∴当x<50时,日销售额随x的增大而增大,
∴当x=30时,日销售额最大,最大值为2100(元),
综上,当0<x≤30时,日销售额的最大值为2100元;
(3)由题意得:
当0<x≤30时,2x≥48,
解得:24≤x≤30,
当30<x≤40时,﹣6x+240≥48,
解得:30<x≤32,
∴当24≤x≤32时,日销售量不低于48件,
∵x为整数,
∴x的整数值有9个,
∴“火热销售期”共有9天.
【变1-2】.某县积极响应市政府加大产业扶贫力度的号召,决定成立草莓产销合作社,负责扶贫对象户种植草莓的技术指导和统一销售,所获利润年底分红.经市场调研发现,草莓销售单价y(万元)与产量x(吨)之间的关系如图所示(0≤x≤100).已知草莓的产销投入总成本p(万元)与产量x(吨)之间满足p=x+1.
(1)直接写出草莓销售单价y(万元)与产量x(吨)之间的函数关系式;
(2)求该合作社所获利润w(万元)与产量x(吨)之间的函数关系式;
(3)为提高农民种植草莓的积极性,合作社决定按0.3万元/吨的标准奖励扶贫对象种植户,为确保合作社所获利润w′(万元)不低于55万元,产量至少要达到多少吨?
解:(1)当0≤x≤30时,y=2.4;
当30≤x≤70时,设y=kx+b,
把(30,2.4),(70,2)代入得,解得,
∴y=﹣0.01x+2.7;
当70≤x≤100时,y=2;
(2)当0≤x≤30时,w=2.4x﹣(x+1)=1.4x﹣1;
当30≤x≤70时,w=(﹣0.01x+2.7)x﹣(x+1)=﹣0.01x2+1.7x﹣1;
当70≤x≤100时,w=2x﹣(x+1)=x﹣1;
(3)当0≤x<30时,w′=1.4x﹣1﹣0.3x=1.1x﹣1,当x=30时,w′的最大值为32,不合题意;
当30≤x≤70时,w′=﹣0.01x2+1.7x﹣1﹣0.3x=﹣0.01x2+1.4x﹣1=﹣0.01(x﹣70)2+48,当x=70时,w′的最大值为48,不合题意;
当70≤x≤100时,w′=x﹣1﹣0.3x=0.7x﹣1,当x=100时,w′的最大值为69,此时0.7x﹣1≥55,解得x≥80,
所以产量至少要达到80吨.
【例2】.心理学家通过实验发现:初中学生听讲的注意力随时间变化,讲课开始时,学生注意力逐渐增强,中间有一段平稳状态,随后开始分散.学生注意力指标数y随时间表t(分钟)变化的函数图象如下.当0≤t≤10时,图象是抛物线的一部分,当10≤t≤20时和20≤t≤40时,图象是线段.
(1)当0≤t≤10时,求注意力指标数y与时间t的函数关系式;
(2)一道数学探究题需要讲解24分钟,问老师能否经过恰当安排,使学生在探究这道题时,注意力指标数不低于45?请通过计算说明.
解:(1)当0≤t≤10时,设抛物线的函数关系式为y=ax2+bx+c.由于它的图象经过点(0,25),(4,45),(10,60),
所以,
解得:,
所以;
(2)当20≤x≤40时,设函数解析式为:y=kx+d,将(20,60),(40,25)代入得:
,
解得:
∴y=﹣x+95,
令y=45,有45=﹣x+95,
解得:x=28,
即讲课后第28分钟时注意力不低于45,
当0≤x≤10时,令y=45,有45=﹣x2+6x+25,
解得:x1=4,x2=20(舍去),
即讲课后第4分钟时,注意力不低于45,
所以讲课后注意力不低于45的时间有28﹣4=24(分钟)>24(分钟),
所以老师可以经过适当的安排,使学生在探究这道数学题时,注意力指数不低于45.
变式训练
【变2-1】.网络销售已经成为一种热门的销售方式,为了减少农产品的库存,我市市长亲自在某网络平台上进行直播销售大别山牌板栗,为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元/kg,每日销售量y(kg)与销售单价x(元/kg)满足关系式:y=﹣100x+5000.经销售发现,销售单价不低于成本价且不高于30元/kg.当每日销售量不低于4000kg时,每千克成本将降低1元,设板栗公司销售该板栗的日获利为w(元).
(1)请求出日获利w与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当w≥40000元时,网络平台将向板栗公司收取a元/kg(a<4)的相关费用,若此时日获利的最大值为42100元,求a的值.
解:(1)当y≥4000,即﹣100x+5000≥4000,
∴x≤10,
∴当6≤x≤10时,w=(x﹣6+1)(﹣100x+5000)﹣2000=﹣100x2+5500x﹣27000,
当10<x≤30时,w=(x﹣6)(﹣100x+5000)﹣2000=﹣100x2+5600x﹣32000,
综上所述:w=;
(2)当6≤x≤10时,w=﹣100x2+5500x﹣27000=﹣100(x﹣)2+48625,
∵a=﹣100<0,对称轴为x=,
∴当6≤x≤10时,w随x的增大而增大,即当x=10时,w最大值=18000元,
当10<x≤30时,w=﹣100x2+5600x﹣32000=﹣100(x﹣28)2+46400,
∵a=﹣100<0,对称轴为x=28,
∴当x=28时,w有最大值为46400元,
∵46400>18000,
∴当销售单价定为28元/kg时,销售这种板栗日获利最大,最大利润为46400元;
(3)∵40000>18000,
∴10<x≤30,
∴w=﹣100x2+5600x﹣32000,
当w=40000元时,40000=﹣100x2+5600x﹣32000,
∴x1=20,x2=36,
∴当20≤x≤36时,w≥40000,
又∵10<x≤30,
∴20≤x≤30,
此时:日获利w1=(x﹣6﹣a)(﹣100x+5000)﹣2000=﹣100x2+(5600+100a)x﹣32000﹣5000a,
∴对称轴为直线x=﹣=28+a,
∵a<4,
∴28+a<30,
∴当x=28+a时,日获利的最大值为42100元,
∴(28+a﹣6﹣a)[﹣100×(28+a)+5000]﹣2000=42100,
∴a1=2,a2=86,
∵a<4,
∴a=2.
【变2-2】.东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p=,且其日销售量y(kg)与时间t(天)的关系如表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
解:(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
解得,
∴y=﹣2t+120.
将t=30代入上式,得:y=﹣2×30+120=60.
所以在第30天的日销售量是60kg.
(2)设第t天的销售利润为w元.
当1≤t≤24时,由题意w=(﹣2t+120)(t+30﹣20)=﹣(t﹣10)2+1250,
∴t=10时,w最大值为1250元.
当25≤t≤48时,w=(﹣2t+120)(﹣t+48﹣20)=t2﹣116t+3360,
∵对称轴t=58,a=1>0,
∴在对称轴左侧w随t增大而减小,
∴t=25时,w最大值=1085,
综上所述第10天利润最大,最大利润为1250元.
(3)设每天扣除捐赠后的日销售利润为m元.
由题意m=(﹣2t+120)(t+30﹣20)﹣(﹣2t+120)n=﹣t2+(10+2n)t+1200﹣120n,
∵在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∵t为整数,图象是孤立的点,
∴﹣>23.5,(见图中提示)
∴n>6.75.
又∵n<9,
∴n的取值范围为6.75<n<9.
1.为了节约水资源,自来水公司按分段收费标准收费,如图所示反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.按照分段收费标准,小颖家三、四月份分别交水费29元和19.8元,则四月份比三月份节约用水( )
A.2吨B.2.5吨C.3吨D.3.5吨
解:当x<10时,设y=mx,
将点(10,22)代入可得:22=10k,
解得:k=2.2,
即可得:y=2.2x,
当x≥10时,设y与x的函数关系式为:y=kx+b(k≠0),
当x=10时,y=22,当x=20时,y=57,
将它们分别代入y=kx+b中得:,
解得:,
那么y与x的函数关系式为:y=3.5x﹣13,
综上可得:y=,
当y=29时,知道x>10,将y=29代入得29=3.5x﹣13,
解得x=12,
当y=19.8时,知道x<10,将y=19.8代入得19.8=2.2x,
解得:x=9,
即可得四月份比三月份节约用水:12﹣9=3(吨).
故选:C.
2.某市为鼓励市民节约使用燃气,对燃气进行分段收费,每月使用11立方米以内(包括11立方米)每立方米收费2元,超过部分按每立方米2.4元收取.如果某户使用9立方米燃气,需要燃气费为 18 元;如果某户的燃气使用量是x立方米(x超过11),那么燃气费用y与x的函数关系式是 y=2.4x﹣4.4 .
解:使用9立方米燃气,需要燃气费为:2×9=18(元);
y=2×11+2.4(x﹣11),即所求的函数解析式为y=2.4x﹣4.4(x>11).
故答案为:18;y=2.4x﹣4.4
3.某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价2元收费;若每月用水量超过14吨,则超过部分每吨按市场价3.5元收费.小明家2月份用水20吨,交水费49元;3月份用水18吨,交水费42元.
(1)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(2)小明家5月份用水30吨,则他家应交水费多少元?
解:(1)由题意可得,
当0≤x≤14时,y=2x,
当x>14时,y=2×14+(x﹣14)×3.5=3.5x﹣21,
由上可得,y与x的函数关系式为y=;
(2)当x=30时,y=3.5×30﹣21=84,
即小明家5月份用水30吨,则他家应交水费84元.
4.某市近期公布的居民用天然气阶梯价格听证会方案如下:
例:若某户2019年使用天然气400立方米,按该方案计算,则需缴纳天然气费为:2.53×360+2.78×(400﹣360)=1022(元)
(1)若小明家2019年使用天然气300立方米,则需缴纳天然气费为 759 元(直接写出结果);
(2)若小红家2019年使用天然气560立方米,则小红家2019年需缴纳的天然气费为多少元?
解:(1)由题意可得,
300×2.53=759(元),
即小明家2019年使用天然气300立方米,则需缴纳天然气费为759元,
故答案为:759;
(2)由题意可得,
360×2.53+(560﹣360)×2.78
=910.8+200×2.78
=910.8+556
=1466.8(元),
答:小红家2019年需缴纳的天然气费1466.8元.
5.在一段长为1000的笔直道路AB上,甲、乙两名运动员均从A点出发进行往返跑训练.已知乙比甲先出发30秒钟,甲距A点的距离y(米)与其出发的时间x(分钟)的函数图象如图所示,乙的速度是150米/分钟,且当乙到达B点后立即按原速返回.
(1)当x为何值时,两人第一次相遇?
(2)当两人第二次相遇时,求甲的总路程.
解:(1)甲开始时的速度为:1000÷4=250(米/分钟),
令250x=150(x+),
解得,x=0.75,
答:当x为0.75分钟时,两人第一次相遇;
(2)当x=5时,
乙跑的路程为:150×(5+)=825<1000,
∴甲乙第二次相遇的时间为:5+=5.5(分钟),
则当两人第二次相遇时,甲跑的总路程为:1000+(5.5﹣5)×=1100(米),
答:当两人第二次相遇时,甲跑的总路程是1100米.
6.“黄金1号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
(Ⅰ)根据题意,填写下表:
(Ⅱ)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;
(Ⅲ)若小张一次购买该种子花费了30元,求他购买种子的数量.
解:(Ⅰ)10,18;
(Ⅱ)根据题意得,
当0≤x≤2时,种子的价格为5元/千克,
∴y=5x,
当x>2时,其中有2千克的种子按5元/千克计价,超过部分按4元/千克计价,
∴y=5×2+4(x﹣2)=4x+2,
y关于x的函数解析式为y=;
(Ⅲ)∵30>10,
∴一次性购买种子超过2千克,
∴4x+2=30.
解得x=7,
答:他购买种子的数量是7千克.
7.电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)分别写出当0≤x≤100和x>100时,y与x的函数关系式;
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电60度,则应缴费多少元?若该用户某月缴费125元时,则该用户该月用了多少度电?
解:(1)当0≤x≤100时,设关系式为y=kx,把(100,65)代入得:k=0.65,
∴y=0.65x(0≤x≤100)
当x>100时,设y与x的函数关系式为y=kx+b,把(100,65)(130,89)代入得:
,解得:k=0.8,b=﹣15,
∴y=0.8x﹣15(x>100)
答:当0≤x≤100和x>100时,y与x的函数关系式分别为y=0.65x(0≤x≤100),y=0.8x﹣15(x>100).
(2)当0≤x≤100时,每度电收费0.65元,当x>100时,每度电收费0.8元.
(3)当x=60时,代入y=0.65x=39元,
当y=125时,代入y=0.8x﹣15得:x=175度,
答:用电60度,则应缴费39元;月缴费125元时,则该用户该月用了175度电.
8.某商品的进价为每件40元,售价每件不低于50元且不高于80元.售价为每件60元时,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.如果每件商品的售价每降价1元,则每个月多卖1件,设每件商品的售价为x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
解:(1)当50≤x≤60时,y=(x﹣40)(100+60﹣x)=﹣x2+200x﹣6400;
当60<x≤80时,y=(x﹣40)(100﹣2x+120)=﹣2x2+300x﹣8800;
∴y=﹣x2+200x﹣6400(50≤x≤60且x为整数)
y=﹣2x2+300x﹣8800(60<x≤80且x为整数);
(2)当50≤x≤60时,y=﹣(x﹣100)2+3600;
∵a=﹣1<0,且x的取值在对称轴的左侧,
∴y随x的增大而增大,
∴当x=60时,y有最大值2000;
当60<x≤80时,y=﹣2(x﹣75)2+2450;
∵a=﹣2<0,
∴当x=75时,y有最大值2450.
综上所述,每件商品的售价定为75元时,每个月可获得最大利润,最大的月利润是2450元.
9.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题.
(1)甲,乙两地的距离为 720 km;慢车的速度为 80 km/h.
(2)求CD段的函数解析式.(不用写自变量的取值范围)
(3)求当x为多少时,两车之间的距离为500km,请通过计算求出x的值.
解:(1)甲、乙两地的距离为720km,慢车的速度为720÷9=80(km/h),
故答案为:720,80;
(2)∵快车的速度为﹣80=120(km/h),
∴快车到达乙地所用时间为=6(h),
此时慢车所行驶的路程是6×80=480(km),
∴C(6,480),
设CD段的函数解析式为y=kx+b,把C(6,480),D(9,720)代入得:
,
解得,
∴CD段的函数解析式为y=80x;
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为500km,
①相遇前:(80+120)x=720﹣500,
解得x=1.1,
②相遇后:
∵点C(6,480),
∴快车到达乙地后,慢车再行驶20km两车之间的距离为500km,
∵慢车行驶20km需要的时间是=0.25(h),
∴x=6+0.25=6.25(h),
∴x=1.1 h或6.25 h,两车之间的距离为500km.
10.某水产市场经营一种海产品,其日销售量y(kg)与销售单价x(元/千克)的函数关系如图所示.
(1)分别求出当20≤x≤30,30<x≤35时,y与x之间的函数关系式.
(2)当单价为32元/千克时,日销售量是多少?
(3)当日销售量为80kg时,单价是多少?
解:(1)当20≤x≤30时,设y与x之间的函数关系式是y=kx+b,
∵点(20,100),(30,50)在该函数图象上,
∴,
解得,
即当20≤x≤30时,y与x之间的函数关系式是y=﹣5x+200;
当30<x≤35时,设y与x之间的函数关系式是y=ax+c,
∵点(30,50),(35,0)在该函数图象上,
∴,
解得,
即当30<x≤35时,y与x之间的函数关系式是y=﹣10x+350;
(2)当x=32时,y=﹣10x+350=﹣10×32+350=30,
即当单价为32元/千克时,日销售量是30千克;
(3)当y=80时,
80=﹣5x+200,
解得x=24,
即当日销售量为80kg时,单价是24元/千克.
11.“低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系式如图1中线段AB所示.在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离x(km)与出发时间t(h)之间的函数关系式如图2中折线段CD﹣DE﹣EF所示.
(1)小丽和小明骑车的速度各是多少?
(2)求点E的坐标,并解释点E的实际意义.
解:(1)由题意可得:小丽速度==16(km/h)
设小明速度为xkm/h
由题意得:1×(16+x)=36
∴x=20
答:小明的速度为20km/h,小丽的速度为16km/h.
(2)由图象可得:点E表示小明到了甲地,此时小丽没到,
∴点E的横坐标==,
点E的纵坐标==
∴点E(,)
12.为加强公民的节水意识,合理利用水资源,某市对居民用水实行阶梯水价.居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系.
(1)写出点B的实际意义;
(2)求线段AB所在直线的表达式,并写出自变量x的取值范围;
(3)某户5月份按照阶梯水价应缴水费108元,其相应用水量为多少立方米?
解:(1)由图可得,
点B的实际意义是当用水25m3时,所交水费为90元;
(2)设一级阶梯用水的单价为x元/m3,则二级、三级阶梯的用水单价分别为1.5x元/m3,2x元/m3,
设点A的坐标为(a,45),
则,
解得,
即点A的坐标为(15,45),
设线段AB所在直线的表达式为y=kx+b,
,
解得,
即线段AB所在直线的表达式为y=4.5x﹣(15<x≤25);
(3)∵108>90,
∴某户5月份的用水量超过25m3,
设该用户5月份用水量为m立方米,
90+(m﹣25)×3×2=108,
解得m=28,
答:其相应用水量为28立方米.
13.如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
(1)求出h与d之间的函数关系式;(不要求写出自变量d的取值范围)
(2)某人身高为196cm,一般情况下他的指距应是多少?
解:(1)设h与d之间的函数关系式为:h=kd+b.
把d=20,h=160;d=21,h=169,分别代入得,.
解得k=9,b=﹣20,即h=9d﹣20;
(2)当h=196时,196=9d﹣20,解得d=24cm.
14.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小王4月份上网20小时,他应付多少元的上网费用?
(3)若小王5月份上网费用为98元,则他在该月份的上网时间是多少.
解:(1)当x≥30时,设y与x之间的函数关系式为y=kx+b,
由题意,
解得,
∴y=x+20.
(2)若小王4月份上网20小时,由图象可知,他应付50元的上网费.
(3)把y=98代入,y=x+20,解得x=78,
∴若小王5月份上网费用为98元,则他在该月份的上网时间是78小时.
15.为提高校园绿化率,美化校园,某示范高中准备购买一批樟树和樱花树,一共100棵,其中樟树不少于10棵.园林部门称樟树成活率为70%,樱花树的成活率为90%,学校要求这批树的成活率不低于80%.樟树的单价y1和购买数量x的函数关系以及樱花树的单价y2和购买数量x的函数关系如图所示.
(1)写出y1关于x的函数关系式;
(2)请你帮学校作个预算,购买这批树最少需要多少钱?
解:(1)当0<x≤60时,设y1=k1x+b1(k1≠0),
把(0,180),(60,60)代入得,
,
∴
∴y1=﹣2x+180(0<x≤60);
当60<x≤100时,y1=60.
综上,y1=﹣2x+180(0<x≤60)或y1=60(60<x≤100);
(2)设购买樟树x棵,则购买樱花树(100﹣x)棵,
由≥80%,得x≤50,
∴10≤x≤50.
设购树所需费用为W元,
当40≤x≤50时,W=(﹣2x+180)x+100(100﹣x)=﹣2(x﹣20)2+10800,
Wmin=﹣2(50﹣20)2+10800=9000(元).
当10≤x<40时,W=(﹣2x+180)x+70(100﹣x)=﹣2(x﹣27.5)2+2×27.52+7000,
Wmin=﹣2×(10﹣27.5)2+2×27.52+7000=7900(元),
综上所述,购树所需费用最少为7900元.
16.A,B两地相距300km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回.如图是两车离A地的距离y(km)与行驶时间x(h)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围.
(2)若两车行驶5h相遇,求乙车的速度.
解:(1)设甲车从A地驶向B地y与x的关系式为y=kx,把(4,300)代入得:
300=4k,解得:k=75,
∴y=75x (0<x≤4)
设甲车从B地返回A地y与x的关系式为y=kx+b,把(4,300)(7,0)代入得:
,解得:k=﹣100,b=700,
∴y=﹣100x+700 (4<x≤7),
答:甲车行驶过程中y与x之间的函数解析式为:y=75x (0<x≤4),y=﹣100x+700 (4<x≤7),
(2)设乙车速度为m千米/小时,则:5m=﹣100×5+700
解得:m=40
答:乙车的速度为40千米/小时.
17.受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”,某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.水果种植专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按2元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.
(1)直接写出当0≤x≤500和x>500时,y与x之间的函数关系式.
(2)若经销商计划一次性购进甲、乙两种水果共1200千克,且甲种水果不少于400千克,但又不超过乙种水果的两倍.问经销商要确保完成收购计划,至少准备多少资金?
解:(1)当0≤≤x≤500时,设y=k1x(k1≠0),根据题意得500k1=1500,
解得k1=3;
∴y=3x;
当x>500时,设y=k2x+b(k2≠0),
根据题意得,,
解得,
∴y=2.5x+250,
∴y=;
(2)购进甲种水果为x千克,则购进乙种水果(1200﹣x)千克,根据题意得:
,
解得400≤x≤800,
当400≤x≤500时,w1=3x+2(1200﹣x)=x+2400.
当x=400时.wmin=2800 元,
当500≤x≤800时,w2=2.5x+250+2(1200﹣x)=0.5x+2650.
当x=500时,wmin=2900 元,
∵2900>2800,
∴当x=400时,总费用最少,最少总费用为2800元.
此时乙种水果1200﹣400=800(千克).
答:购进甲种水果为400千克,购进乙种水果800千克,才能使经销商付款总金额w(元)最少,至少准备2800元资金.
18.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时主变化如图所示,当成人按规定剂是服药后,
(1)分别求出x<2和x>2时y与x的函数关系式,
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
解:(1)当x≤2时,设y=k1x,
把(2,6)代入上式,得k1=3,
∴x≤2时,y=3x;
当x>2时,设y=k2x+b,
把(2,6),(10,3)代入上式,
得k2=﹣,b=.
∴x≥2时,y=﹣x+.
(2)把y=4代入y=3x,得x1=,
把y=4代入y=﹣x+,得x2=.
则x2﹣x1=6小时.
答:这个有效时间为6小时.
19.甲骑电瓶车,乙骑自行车从西山漾公园丝绸小镇门口出发沿同一路线匀速前往太湖龙之梦乐园,设乙行驶的时间为x(h),甲、乙两人距出发点的路程s甲、s乙关于x的函数图象如图①所示,甲、乙两人之间的路程差y关于x的函数图象如图②所示,请你解决以下问题:
(1)甲的速度 25 km/h,乙的速度是 10 km/h;
(2)对比图①、图②可知:a= 10 ,b= ;
(3)乙出发多少时间,甲、乙两人路程差为7.5km?
解:(1)由图可得,
甲的速度为:25÷(1.5﹣0.5)=25÷1=25km/h,乙的速度为:25÷2.5=10km/h,
故答案为:25,10;
(2)由图可得,
a=25×(1.5﹣0.5)﹣10×1.5=10,
25(b﹣0.5)=10b,得b=,
故答案为:10,;
(3)由题意可得,
前0.5h,乙行驶的路程为:10×0.5=5<7.5,
则甲、乙两人路程差为7.5km是在甲乙相遇之后,
设乙出发xh时,甲、乙两人路程差为7.5km,
25(x﹣0.5)﹣10x=7.5,
解得,x=,
25﹣10x=7.5,得x=,
即乙出发h或h时,甲、乙两人路程差为7.5km.
20.某校的甲、乙两位老师同住一小区,该小区与学校相距2400米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校又骑行若干米到达还车点后,立即步行走回学校.已知甲步行的速度比乙步行的速度每分钟快5米.设甲步行的时间为x(分),图1中线段OA和折线B﹣C﹣D分别表示甲、乙离开小区的路程y(米)与甲步行时间x(分)的函数关系的图象;图2表示甲、乙两人之间的距离s(米)与甲步行时间x(分)的函数关系的图象(不完整).
根据图1和图2中所给信息,解答下列问题:
(1)甲步行的速度 80米/分 ,乙出发时甲离小区的距离 800米 ;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,求出当25≤x≤30时s关于x的函数关系式.
解:(1)由图可得,
甲步行的速度为:2400÷30=80(米/分),
乙出发时甲离开小区的路程是10×80=800(米),
故答案为:80米/分,800米;
(2)设直线OA的解析式为y=kx,
30k=2400,得k=80,
∴直线OA的解析式为y=80x,
当x=18时,y=80×18=1440,
∴乙骑自行车的速度为:1440÷(18﹣10)=180(米/分),
∵乙骑自行车的时间为:25﹣10=15(分钟),
∴乙骑自行车的路程为:180×15=2700(米),
当x=25时,甲走过的路程为:80×25=2000(米),
∴乙到达还车点时,甲乙两人之间的距离为:2700﹣2000=700(米),
答:乙骑自行车的速度是180米/分,乙到达还车点时甲、乙两人之间的距离是700米;
(3)乙步行的速度为:80﹣5=75(米/分),
乙到达学校用的时间为:25+(2700﹣2400)÷75=29(分),此时甲还要1分钟到学校,即甲离学校80米,
∴当25≤x≤30时s关于x的函数的大致图象如图:
当25≤x≤29时,设s=mx+n,将(25,700),(29,80)代入得:
,
解得,
∴s=﹣155+4575;
当29<x≤30时,设s=px+q,将(29,80),(30,0)代入得:
,
解得,
∴s=﹣80x+2400,
∴s=.
时间t(天)
1
3
6
10
20
40
…
日销售量y(kg)
118
114
108
100
80
40
…
第一档天然气用量
第二档天然气用量
第三档天然气用量
年用天然气量360立方米及以下,价格为每立方米2.53元
年用天然气量超出360立方米,不超600立方米时,超过360立方米部分每立方米价格为2.78元
年用天然气量600立方米以上,超过600立方米部分价格为每立方米3.54元
购买种子的数量/kg
1.5
2
3.5
4
…
付款金额/元
7.5
10
16
18
…
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
专题58 二次函数中的面积问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份专题58 二次函数中的面积问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含专题58二次函数中的面积问题原卷版docx、专题58二次函数中的面积问题解析版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
专题57 二次函数中的线段最值问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份专题57 二次函数中的线段最值问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含专题57二次函数中的线段最值问题原卷版docx、专题57二次函数中的线段最值问题解析版docx等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。
专题56 一次函数中的倍、半角问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份专题56 一次函数中的倍、半角问题(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含专题56一次函数中的倍半角问题原卷版docx、专题56一次函数中的倍半角问题解析版docx等2份试卷配套教学资源,其中试卷共70页, 欢迎下载使用。












