2024年初三中考第一次模拟考试试题：数学（泰州卷）（全解全析）

这是一份2024年初三中考第一次模拟考试试题：数学（泰州卷）（全解全析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第Ⅰ卷
一、选择题（本大题共6个小题，每小题3分，共18分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
1．的相反数是（ ）
A．B．C．D．
【答案】B
【解析】解：的相反数是．故选：B．
2．中国古代数学名著《九章算术注》中记载：“邪解立方，得两堑堵．”意即把一长方体沿对角面一分为二，这相同的两块叫做“堑堵”．如图是“堑堵”的立体图形，它的左视图为（ ）
A．B．
C．D．
【答案】C
【解析】解：由题意得：它的左视图为一个三角形，如图：
，
故选：C．
3．张明在对一组数据“6，15，28，63，39，28”进行分析时，发现第一个两位数的个位数字被墨水弄脏看不到了，此时统计结果不受影响的统计量是（ ）
A．方差B．众数C．平均数D．中位数
【答案】D
【解析】解：这组数据的平均数、方差和众数都与被涂污数字有关，而这组数据的中位数为28与39的平均数，与被涂污数字无关．
故选：D．
4．如图，直线，直角三角形如图放置，，若，则的度数为（ ）
A．B．C．D．
【答案】A
【解析】解：如图，
，，，
，
，
故选：A．
5．下列命题正确的是（ ）
A．对角线相等的四边形是矩形B．对角线互相垂直且相等的四边形是正方形
C．顺次连接菱形各边中点所得的四边形是正方形D．菱形的面积为两条对角线长度乘积的一半
【答案】D
【解析】A、等腰梯形的对角线相等，但它不是矩形，故该选项不符合题意；
B、对角线互相平分、垂直且相等的四边形是正方形，故该选项不符合题意；
C、顺次连接菱形各边中点所得的四边形是矩形，故该选项不符合题意；
D、菱形的面积为两条对角线长度乘积的一半，符合题意；
故选：D
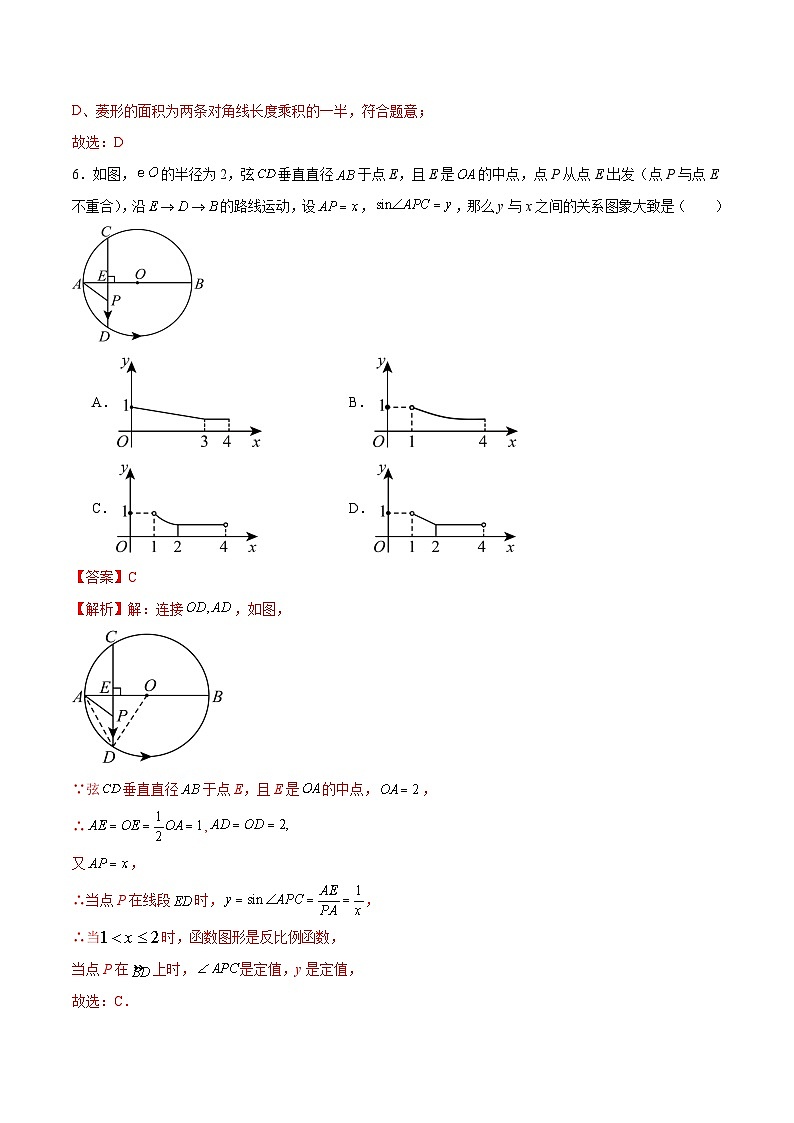
6．如图，的半径为2，弦垂直直径于点E，且E是的中点，点P从点E出发（点P与点E不重合），沿的路线运动，设，，那么y与x之间的关系图象大致是（ ）
A．B．
C．D．
【答案】C
【解析】解：连接，如图，
∵弦垂直直径于点E，且E是的中点，，
∴,
又，
∴当点P在线段时，，
∴当时，函数图形是反比例函数，
当点P在上时，是定值，y是定值，
故选：C．
第Ⅱ卷
二、填空题（本大题共10个小题，每小题3分，共30分）
7．分解因式： ．
【答案】
【解析】解：；
故答案为：
8．国家铁路集团有限公司（简称“国铁集团”）最新数据显示，11月份，国家铁路发送煤炭1.78亿吨．“1.78亿”用科学记数法表示为 ．
【答案】
【解析】解：将1.78亿用科学记数法表示为：．
故答案为：．
9．物理课上我们学习过凸透镜成像规律．如图，蜡烛AB的高为，蜡烛与凸透镜的距离为，蜡烛的像与凸透镜的距离为，则像的高为 ．
【答案】
【解析】解：，
，
，
,
的高为,为,为,
，
故答案为：
10．已知圆锥展开图的圆心角为，母线长为5，则该圆锥的体积为 ．
【答案】
【解析】解：如图：设该圆锥的底面半径为r，

根据题意得，解得，
圆锥的高为：，
根据圆锥的体积公式
得到该圆锥的体积为：，
故答案为：．
11．一只蜘蛛爬到如图所示的一块瓷砖上，并随机停留在某一位置上，则它停留在阴影区域上的概率是 ．
【答案】
【解析】解：设一块瓷砖的面积为，
则，
则它停留在阴影区域上的概率是，
故答案为：．
12．如图，平分，，的延长线交于点E，若，则的度数为 ．
【答案】/80度
【解析】解：平分，
，
又，
，
，
，
，
故答案为：．
13．如图，工人师傅用扳手拧形状为正六边形的螺帽，现测得扳手的开口宽度，则螺帽边长 .
【答案】
【解析】解：如图：连接，过点B作于D，
，
由正六边形可得：,
∴，
由，则，
∵在中，，
∴,
∴
∴，
∴．
故答案为．
14．在《代数学》中记载了求方程正数解的几何方法：如图①，先构造一个面积为的正方形，再以正方形的边为一边向外构造四个面积为2x的矩形，则图中大正方形的面积为，则该方程的正数解，小明尝试用此方法解关于x的方程时，构造出如图②所示的正方形．已知图②中阴影部分的面积和为55，则该方程的正数解为 ．
【答案】/
【解析】如图2所示：
先构造一个面积为的正方形，再以正方形的边为一边向外构造四个面积为的矩形，得到大正方形的面积为，则该方程的正数解为．
故答案为：
15．平面直角坐标系中，在轴上，且到一条抛物线的顶点及该抛物线与轴的交点的距离之和最小的点，称为这条抛物线与轴的“亲密点”，那么抛物线与x轴的“亲密点”的坐标是 ．
【答案】
【解析】解：，
抛物线开口向上，顶点为，
顶点关于轴的对称点为，
当时，，
抛物线与轴的交点为，
设直线的解析式为，
代入得，，
解得，
直线的解析式为，
令，则
抛物线与轴的“亲密点”的坐标是，
故答案为：．
16．如图，已知矩形，，，点N是边上一点，且，将矩形绕A顺时针旋转（），得到矩形，点B的对应点是点E，点C的对应点是点F，点D的对应点是点G，连接．点M是的中点，连接，在旋转过程中，线段的最大值为 ．
【答案】
【解析】连接，交于点O，连接，，过点作于点，连接，
∵是矩形，
∴，
∵点M是的中点，
∴是的中位线，
∴，
∴点M在以为圆心，以为半径的圆上运动，
∵，
∴，
∵，，
∴，
∴
∴
∴，，
∵，
∴，
在中，
∴线段的最大值为
故答案为：．
三、解答题（本大题共10个小题，共102分．解答应写出文字说明，证明过程或演算步骤）
17．（1）计算: ；
（2）解方程:．
【解析】（1）
，
（2）
原方程去分母得：
去括号得：，
移项，合并同类项得：，
系数化为1得： ，
检验：将代入得，
故原方程的解为：
18．2023年11月24日，第十届【媒眼看国茶】论坛：文明互鉴，“一带一路”共筑茶缘在中国举行．为了解A、B两种铁观音茶叶的亩产量，工作人员从两种类型的铁观音中各随机抽取10亩，在完全相同条件下试验，统计了茶叶的亩产量（单位：千克/亩），并进行整理、描述和分析（亩产量用x表示，共分为三个等级：合格，良好，优秀），下面给出了部分信息：
10亩A型铁观音茶叶的亩产量：50，54，55，55，55，57，57，58，59，60．
10亩B型铁观音茶叶中“良好”等级包含的所有数据为：57，57，57，59．
抽取的A、B型铁观音亩产量统计表
B型铁观音茶叶亩产量扇形统计图
根据以上信息，解答下列问题：
(1)填空：a=_________，b=________________，m=_____________
(2)根据以上数据，你认为哪款茶叶更好？请说明理由（写出一条理由即可）；
(3)若某市今年种植B型铁观音茶叶3000亩，估计今年B型铁观音茶叶亩产量在“良好”等级及以上的有多少亩？
【解析】（1）在50，54，55，55，55，57，57，58，59，60中，出现次数最多的是55，
众数，
型中“良好”等级有4个，占，“优秀”等级所占百分比为，
“合格”等级占，即，
把型数据从小到大排列后，第5个和第6个数都是57，
；
故答案为：55，57，40；
（2）款茶叶更好，
理由：因为款茶叶的中位数和众数都大于款茶叶的，所以款茶叶更好（答案不唯一）；
（3）（亩，
答：估计今年型铁观音茶叶亩产量在“良好”等级及以上的有2400亩．
19．为弘扬中华传统文化，某地近期举办了中小学生“国学经典大赛”．比赛项目为：A．唐诗；B．宋词；C．论语；D．三字经．比赛形式分“单人组”和“双人组”．
(1)小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率为_____，是_____事件（填“随机”或“不可能”或“必然”）？
(2)小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少？请用画树状图或列表的方法进行说明．
【解析】（1）解：小丽随机抽取一个比赛项目，共有4种等可能的结果，其中恰好抽中“三字经”的情况只有1种，
∴，是随机事件；
故答案为：，随机；
（2）画出树状图如图：
由图可知，共12种等可能的结果，其中小红抽中“唐诗”且小明抽中“宋词”的情况只有1种，
∴．
20．如图，是的直径，点C在上，且，．
(1)尺规作图：过点O作的垂线，垂足为E，交劣弧于点D，连接（保留作图痕迹，不写作法）；
(2)在（1）所作的图形中，分别求和的长．
【解析】（1）解：分别、以为圆心，大于的长为半径画弧交于点，连接，与圆的交点即为，则即为的垂线，连接，如图即为所求；
（2）由（1）可知，，则，即点为的中点，
∵，
∴为的中位线，
∴，
∵是的直径，
∴，
由勾股定理可得：，
∴，则，
由勾股定理可得：．
21．乐乐超市为了元旦促销，印制一批宣传册．该宣传册每本共10页，由A，B两种彩页构成．已知A种彩页制版费为3元/张，B种彩页制版费为2元/张，共计24元（注：彩页制版费与印数无关）．
(1)每本宣传册A，B两种彩页各有多少张？
(2)据了解，A种彩页印刷费为元/张，B种彩页印刷费为元/张，这批宣传册的制版费与印刷费的和不超过594元．如果按到超市的顾客人手一册发放宣传册，那么最多能发多少位顾客？
【解析】（1）解：设每本宣传册中种彩页有页，种彩页有页，
∴，
解得，，
∴每本宣传册中种彩页有张，种彩页有张；
（2）解：设可以发位顾客，
∴，
解得，，
∴最多可以发位顾客．
22．金秋十一月，阳光大草坪正处于草坪养护阶段，如图为草坪的平面示意图．经勘测，入口B在入口A的正西方向，入口C在入口B的正北方向，入口D在入口C的北偏东方向处，入口D在入口A的北偏西方向处．（参考数据）
(1)求的长度；（结果精确到1米）
(2)小明从入口D处进入前往M处赏花，点M在上，距离入口B的处．小明可以选择鹅卵石步道①，步行速度为，也可以选择人工步道②，步行速度为，请计算说明他选择哪一条步道时间更快？（结果精确到）
【解析】（1）过点作于点，过点作于点，
则，，，，，
在中，，
，
在中，，
．
的长度为．
（2）由（1）知，，
，
，
在中，，
在中，，
．
鹅卵石步道的路程为，
所需时间为．
人工步道的路程为，
所需时间为．
，
他选择人工步道时间更快．
23．如图，过正方形顶点B，C的与相切于点E，与相交于点F，连接．

(1)求证：平分．
(2)若，，求的长．
【解析】（1）证明：如图，连接，

与相切于点，
，即，
四边形是正方形，
，
，
，
，
，
，
平分．
（2）解：如图，连接，

四边形是正方形，
，，
是的直径，
，
由（1）已证：，
，
，
，
，
∴设，则，
，
，
则在中，．
24．如图，在平面直角坐标系中，直线与双曲线交于两点，与轴交于点，与轴交于点，其中点的坐标为．
(1)求双曲线和直线的表达式；
(2)将直线向下平移，当平移后的直线与双曲线只有一个交点时，请求出直线的解析式；
(3)在轴上是否存在点使得？若存在，请求出点的坐标；若不存在，请说明理由．
【解析】（1）解：把代入得，
则双曲线的表达式是，
把代入得，
解得，
则直线的表达式是；
（2）解：将直线向下平移个单位长度得直线解析式为，
∵直线向下平移个单位长度后与反比例函数的图象只有一个交点，
∴，
整理得，
，
解得或，
∴直线的解析式为或；
（3）解：存在，
过点作轴于点，
∵点的坐标为，
，
∵直线的表达式是，
令，则，
解得，
，
，
是等腰直角三角形，
以为圆心，为半径作，与轴交于点，连接，
，
设，
，
，
∴点的坐标为或．
25．如图，抛物线（其中）与x轴交于A、B两点，交y轴于点C．

(1)求的度数和线段的长（用a表示）：
(2)若点D为的外心，且与的周长之比为，求此抛物线的解析式；
(3)在（2）的前提下，试探究抛物线上是否存在一点P，使得?若存在，求出点P的坐标；若不存在，请说明理由．
【解析】（1）解：在中，当，即，解得或，
，
∴
在中，当时，得到，
，
，
，
．
（2）解：由（1）知，
点D是的外心，
，
∴，
，
∵与的周长之比为，
，
，
解得或（舍去），
∴抛物线的解析式为．
（3）解：如图3-1，作点C关于直线的对称点，连接，过点作轴于H，

由（2）得，，抛物线对称轴为直线，
∴，且点在抛物线上，
∴，，
∴，
又∵，
∴，
，
，
，
点就是所求的点P，
．
如图3-2所示，作点P关于直线的对称点E，则，作直线交抛物线于，

由对称性质可知，，，
∵，
∴轴，即，，
∵，
∴，
，
点E在y轴上，
∴，
，
，
∴直线的解析式为，
联立，解得或，
，
综上所述，满足条件的点P的坐标为或．
26．某“数学学习兴趣小组”成员在复习《图形的变化》时，对下面的图形背景产生了浓厚的兴趣，并尝试运用由“特殊到一般”的思想进行了探究：
〖问题背景〗如图1，正方形中，点E为边上一点，连接，过点作交边于点，将沿直线折叠后，点落在点处，当，则 °．
〖特例探究〗如图2，连接，当点恰好落在上时，求证：．
〖深入探究〗如图3，若把正方形改成矩形，且，其他条件不变，他们发现与之间也存在着一定的数量关系，请直接写出与之间的数量关系式．
〖拓展探究〗如图4，若把正方形改成菱形，且，，其他条件不变，当时，请直接写出的长．
【解析】〖问题背景〗解：，，
，
将沿直线折叠后，点落在点处，
，
，
故答案为：25；
〖特例探究〗证明：将沿直线折叠后，当点恰好落在上时，
，，，
，
，
，
又，
，
，，
，
，
，
，
，
；
〖深入探究〗解：将沿直线折叠后，当点恰好落在上时，
，，，
，
，
，
又，
，
，，
，
，
，
，
，
，
；
〖拓展探究〗解：如图4，在上截取，连接，在上截取，连接，
四边形是菱形，，
，，
，，
是等边三角形，
，，
，
设，
，，
，，
，
，
，
将沿直线折叠后，当点恰好落在上时，
，，，，
，
，
又，，
，
，，
，
，
，
又，
是等边三角形，
，
设，，
，
，，
，，
，
，（负值舍去），
，，
．
又∵，
∴．型号
A
B
平均数
56
56
中位数
56
众数
57
方差
7.4
15.8
“优秀”等级所占百分比
10%
20%