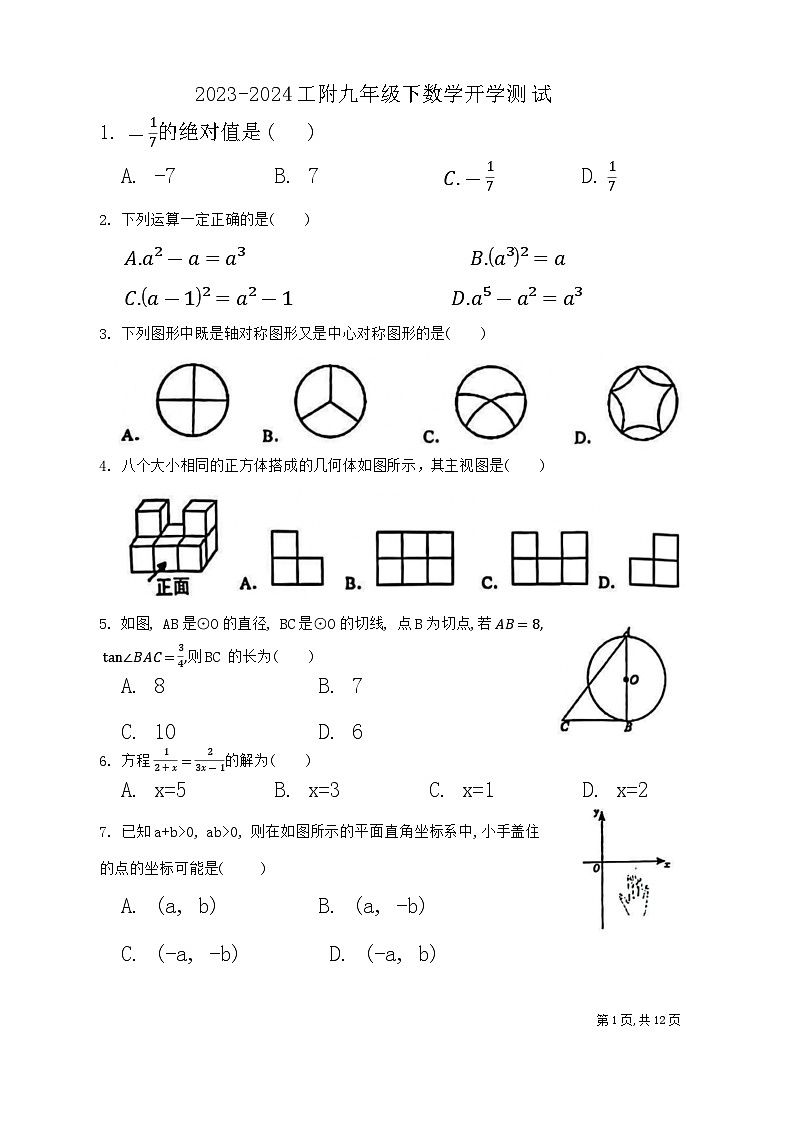
黑龙江省哈尔滨工业大学附属中学校2023-2024学年九年级下学期开学考试数学试卷(五四制)

这是一份黑龙江省哈尔滨工业大学附属中学校2023-2024学年九年级下学期开学考试数学试卷(五四制)，共13页。试卷主要包含了 -17的绝对值是， 下列运算一定正确的是， 周日等内容，欢迎下载使用。

A. -7 B. 7 C.-17 D. 17
2. 下列运算一定正确的是( )
A.a²-a=a³ B.a³²=a
C.a-1²=a²-1 D.a⁵-a²=a³
3. 下列图形中既是轴对称图形又是中心对称图形的是( )
4. 八个大小相同的正方体搭成的几何体如图所示，其主视图是( )
5. 如图, AB是⊙O的直径, BC是⊙O的切线, 点B为切点,若 AB=8,tan∠BAC=34,则BC 的长为( )
A. 8 B. 7
C. 10 D. 6
6. 方程 12+x=23x-1的解为( )
A. x=5 B. x=3 C. x=1 D. x=2
7. 已知a+b>0, ab>0, 则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A. (a, b) B. (a, -b)
C. (-a, -b) D. (-a, b)
第1页,共12页8. 一个不透明的袋子中装有12个小球，其中8个红球、4个黄球，这些小球除颜色外无其它差别，从袋子中随机换出一个小球。.则摸出的小球是红球的概率是( )
A. 12 B. 13 C.112 D. 23
9.’如图, 在△ABC中, DE∥BC、AD=2, BD=3,AC=10, 则AE的长为( )
A. 3 B. 4
C.5 D.6
10. 周日。小辉从家步行到图书馆读书，读了一段时间后，小辉立刻按原路回家。在整个过程中，小辉离家的距离s(单位：m)与他所用的时间t(单位：min)之间的关系如图所示，则小辉从家去图书馆的速度和从图书馆回家的速度分别为( )
A. 75m/min, 90m/min B. 80m/min, 90m/min
C. 75m/min, 100m/min D. 80m/min。100m/min
二、填空题(每小题3分，共计30分)
11. 风能是一种清洁能源，我国风能储量很大，仅陆地上风能储量就有253000兆瓦，用科学记数法表示为 兆瓦。
12. 在函数 y=x5x+3中，自变量x的取值范围是 .
13.9的算术平方根是 .
14. 把多项式. xy²-9x分解因式的结果是 .
15. 不等式组 3x+4>04-2x<-1的解集是 .
16. 二次函数y=- (x-6)2+8的最大值是 .
17. 若双曲线 y=k-1x的图象的一支位于第四象限，则k的取值范围是 .
18. 一个扇形的面积为7πcm²，半径为6cm，则此扇形的圆心角是 度.
19. 在△ABC中, ∠A=50°, ∠B=30°, 点D在AB边上, 连接CD, 若△ACD为直角三角形，则∠BCD的度数为 度.
第2页,共12页20.如图，矩形ABCD的对角线BD的垂直平分线交 AD于点E，交 BC于点F, 连接CE, △ECF 的面为 103,ln∠ADB=23,则CD的长为 .
三、解答题(其中21~22题各7分, 23-24题各8分, 25~27题各10分, 共计60分)
21. 先化简再求值： x+2x-2-x2-2xx2-4x+4÷x-4x-2, 其中 x=4tan45°+2cs30°
22.如图。方格纸中每个小正方形的边长均为1个单位长度，△ADC 的顶点和线段DE的端点均在小正方形的顶点上。
(1) 在方格纸中将△ABC向上平移1个单位长度，再向右平移2个单位长度后得到△MNP(点A的对应点是点M，点B的对应点是点N，点C 的对应点是点 P)，请画出△MNP:
(2) 在方格纸中画出以DE为斜边的等腰直角三角形DEF(点F在小正方形的顶点上).连接FP，请直接写出线段FP的长。
23. 某中学开展以“我最喜欢的健身活动”为主题的调查活动，围绕“在跑步类、球类、武术类、操舞类四类健身活动中，你最喜欢哪一类? (必选且只选一类)”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢操舞类的学生人数占所调查人数的 25%. 请你根据图中提供的信息解答下列问题：
(1) 在这次调查中，一共抽取了多少名学生?
(2) 请通过计算补全条形统计图；
(3) 若该中学共有1600 名学生，请你估计该中学最喜欢球类的学生共有多少名。24. 已知四边形ABCD是正方形, 点E在边 DA 的延长线上, 连接CE交AB于点 G, 过点B作 BMI⊥CE,,垂足为点M, BM的延长线交AD于点 F, 交 CD的延长线于点 H.
(1) 如图1, 求证:( CE=BH;
(2) 如图2, 若 AE=AB，连接CF，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形( (△AEG除外)，使写出的每个三角形都与 △AEG全等.
25. 某中学计划为书法小组购买某种品牌的A、B两种型号的毛笔. 若购买3支A种型号的毛笔和1支B种型号的毛笔需用 22 元；若购买2支A种型号的毛笔和3支B 种型号的毛笔需用24 元.
(1) 求每支A种型号的毛笔和每支B种型号的毛笔各多少元：
(2) 该中学决定购买以上两种型号的毛笔共80支，总费用不超过420元，那么该中学最多可以购买多少支A种型号的毛笔?
第4页,共12页26. 如图, △ABC内接于⊙O, 半径AO平分. ∠BAC,,延长AO 交BC于点K.
(1) 如图 1, 求证: BK=CW;
(2) 如图2, 延长AK 交⊙O于点D, 当. AK=3DK时, 求证: △ABC为等边三角形；
(3) 如图3, 在(2) 的条件下, 点 E 在弧AB 上, 点 F 在弧 CD上, 连接 AF、AE、BE、CE, EC 交 AF 于点P, AF⊥AR,且 AF=CB,, 连接 DF, 当1 DF=2时, 求 BE的长.
第5页,共12页27.如图，在平面直角坐标系中，点O为坐标原点，抛物线 y=ax²-2ax-3aa≠0交x轴的负半轴于点A，交 x轴的正半轴于点B，交y轴的正半轴于点C，且( OB=2OC.
(1) 求a的值:
(2) 点D 为抛物线的顶点，点P在第三象限的抛物线上， PQ‖y轴, PQ交直线BD于点Q. 设点P 的横坐标为t，线段PQ的长为d，求d与t的函数关系式：
(3) 在(2) 的条件下, 连接PB、PA, PB 交y轴于点E, 连接DE、AE, 将线段DE绕点D逆时针旋转 90° 得到线段 DF, 射线FB交y轴于点K, 当 ∠PAB-∠EBK=∠APE时， 求点P 的坐标.
第6页,共12页2023-2024工附九 (下) 数学03 开学测参考答案
一、 选择题
二、填空题
三、解答题
21.原式: =x+2x-2-xx-2x-22×x-2x-4=x+2)x-2-xx-2x-22×x-2x-4
=x-2x+2-xx-22×x-2x-4=2x-2x-22×x-2x-4=2x-4
22. 解:
(1) 如图
2FP=5
23. 解:
(1) 20÷25%=80 (名)
答：在这次调查中一共抽取了 80名学生。
(2) 80-16-24=20 (名)
答：最喜欢武术类的有20名学生。
(3) 24÷80×1600=480 (名)
答：由样本估计总体，该中学最喜欢球类的学生大约有480名。
24. 证明:
(1) ∵正方形ABCD,∴∠ADC=90° ,∠BCD=90° ,BC=CD
∴∠EDH=180°-∠EDC=180°-90°=90°
∵BM⊥CE, ∴∠EMF=90°
∴∠EMH=∠EDH, ∴∠EFH-∠EDH=∠EFH-∠EMH
∴∠E=∠H
∵∠EDC=∠BCH=90° ,CD=CB
∴△BCH≌△CDE(AAS), ∴CE=BH
(2) △ABF;△DCF;△BCG;△DHF
25. 解:
(1)设，每支 A种型号毛笔a 元，每去B种型号毛笔 b元。
第7页,共12页1
2
3
4
5
6
7
8
9
10
D
A
A
C
D
A
B
D
B
C
11
12
13
14
15
2.53×10⁵
x≠-3/5
3
x(y+3)(y-3)
x>5/2
16
17
18
19
20
8
k<1
70
10°或60°
4
3a+b=222a+3b=24 解得， a=6b=4第8页,共12页
答：每去A种型号毛笔6元，B种型号毛笔4元。
(2)设，该中学购买m 支A种型号毛笔。
6m+4(80-m) <420
m≤50
答：该中学最多可以购买50支A种型号毛笔。
26. 证明:
①连OL, OB
∵OA=OC,∴∠1=∠3
∵OA=OB, ∴∠2=∠4
∵AO 平分∠CAB, ∴∠1=∠2, ∴∠3=∠4
又∵OA=OA, ∴△OAC≌△OAB, ∴AC=AB
∵∠1= ∠2, ∴BK=CK
②连OC, CD
设DK=t,则 AK=3DK=3t
∴AD=AK+DK=3t+t=4t
∴AO+OD=1/2AD=1/2×4t=2t
∴OK=OD-DK=2t-t=t
∴OK=DK
∵AC=AB,∠CAO=∠BA
∴AK⊥CB
∵CB垂直平分OD,∴OC=CD
∵OC=CD, ∴OC=OD=CD, ∴△COD是等边三角形
∴∠D =60°
⊙O中, AC=AC,∴∠B=∠D=60∘
∵AC=AB, ∴△ABC为等边三角形。
③连DE, 作DT⊥AE 于T
∵AD是⊙O直径, ∴∠AFE=∠AED=90°
∵AF⊥AE,∴∠EAF=90°,∴∠EAF=∠AFD=∠AED=9
∴四边形 AEDF是矩形
∴AE= DF=2
⊙O 中, AE=AF,∴AE=DF
⊙O中, AF=CD,∴AF=CE
∵AC=AC,∴AE=CF,又∵ AE=OF∴CF=DF
⊙O 中, CF=DF,∴∠CAF=∠DAF
∵△ABC为等边三角形, ∴∠CAB=∠ACB=60°
∵AD 平分∠CAB,
∴∠CAD=∠BAD=1/2∠CAD=1/2×60°=30°
∴∠CAF=∠DAF=1/2∠CAD=1/2×30°=15°
⊙O中, CF=AD,∴∠ACE=∠CAF=15∘
∴∠ECB=∠ACB-∠ACE=60°-15°45°
⊙O 中, BE=BE,∴∠EAB=∠ECB=45∘
∵四边形 ACBE 内接于⊙O,
∴∠AEB+ ∠ACB=180° ,
∴∠AEB=180°-∠ACB=180°-60°=120°
∴∠TEB=180°-∠AEB=180°-120°=60°
设BE=m, 则AT=AE+ET=2+m,
Rt△ETBk , ∠T=90°
tan∠TEB=BT/ET=tan60∘=3
∴BT=3ET=3m
Rt△ATB 中, ∠T=90°
tan∠TAB=BT/AT=tan45°=1
∴AT=BT,∴2+m=3m,∴m=3+1
Rt△ETB 中, ∠T=90°
cs∠TEB=ET/BE=cs60°=1/2
∴BE=2ET=2m=2×3+1=23+2
27. 解
(1)设, Ax₁0,Bx₂0(x₁ ∵0=ax²-2ax-3a,a≠0,∴x₁=-1,x₂=3
∴A(-1,0),B(3,0)
∴OB=3, ∵OE =20C
∴OC=1/2OB=1/2×3=3/2
∴C(0,3/2)
2y梯=-12x2-2×-12x-3×-12
即 y=-12x2+x+32 一
∴顶点D 横坐标： xD=-b2a=-12×1-12=1
∴D1-12×12+1+32+1+3)即D (1, 2)
设 y[D=kx+b
则 解得， k=-1b=3∴yBD=-x+3
P(t,-12t2+t+32
设PQ交OA于T
∵PQ∥CO, ∴∠QTO=∠COB=90°
第9页,共12页∴PQ⊥x轴, ∴x0=xP=t,∴y0=-t+3
∴PQ=yQ-yP=-t+3--12t2+t+32=12t2-2t+32
∴d=12t2-2t+32
(3)【双解】：双解原因在于点K可能在E下方，亦可在E 上方，造成 ∠FB2=43∘或解1° (1°表示情况1，这是通用的数学语言)
连 AD, 作 DM⊥AB于 M
∵D (1, 2), ∴OM=1,DM=2
∵A (-1, 0) ∴OA=1
∴AM=AO+0)M=1+1=2,BM=BO-0M=3-1=2
∴AM=BM
∵BM⊥AB,∴∠AMD=90°, ∴DM垂直平分 AB
∴AD=BD,又DM =BM=2
∴∠MDB=∠MBD=1/2∠AMD=1/2×90° =45°
∵AD=BD, ∴∠DAB=∠DBA=45°
∴∠ADB=180°-∠DAB-∠DBΛ=180°-45°-45°=90°
∵DE 绕点D 逆时针旋转PDF, ∴DE=DF,DE⊥DF
∴∠EDF=90° ,∴∠EDF=∠ADB
∴∠EDF-∠EDB=∠ADB-∠EDB
∴∠ADE= ∠BDF
∵AD=BD,DE=DF ∴△ADE≌△BDF(SAS)
∴∠DBF=∠DAE
延长AE交 BK 于K
∵∠DBF+∠KBD=180° ,∴ RBD+∠DAR=180°
∴∠ARB=(4-2)×180°-∠ADB-(∠DAR+∠DBK)=360°-90°-180° =90°设∠EBK=a则∠ ∠BER=180°-∠ERB-∠EBR=180°-90°-a=90°-a
∴∠AEP=∠REB=90°-a
设∠APE=m,
∵∠PAE-∠EBK=∠APE
∴∠PAE=∠EBK +∠APE=a+m
∴∠PAE+∠APE+∠AEP=a+m+m+90°-a=180° ∴m=45° ∴∠APE=45°
作 AW⊥AP,交BP于W, 则∠PAW=90° ,
则∠ ∠AWP=180°-∠PAW-∠APW=180°-90°-45°=45°
∴∠PWA=∠ADW, ∴AP=AW
由(2)知AT⊥PT,∴∠PTA=90°
作WN⊥AB于N, 则∠ANW=90°,又∠PAW=∠ATP
第10页,共12页∴∠WAN=∠PAN-∠PAW=∠PAN-∠PTA=∠APT
又∵∠ATP=∠ANW,AP=AW
∴△APT≌△WAN
∴P=t-12t2+t+32则( 0T=-t,AT=0T-AO=-t-1
∴WN=AT=-t-1
设直线B P 解析式: yBP=px+q
-12t2+t+32=tp+q0=3p+q
∵t-3≠0
∴p=-12-t2q=32+32t
设, E(0, yE)
则 yE=0×-12-t2+32+32t=32+32
∴E032+32t∴OE=-32-32t
∵WN⊥AB,∴∠WNB=90°
∴∠WNB=∠EOB, ∴WN∥OE
∴△WNB∽△EOB, ∴BN/OB=WN/OE,
即 BN3=-1-t-32-32t+∴-32-32t≠0∴BN=2
∴ON=OB-BN=3-2=1,AN=AO+ON=1+1=2
∵△ATP≌△WAN, ∴PT=AN=2
∴ yp =-2,即 -12t2+t+32=-2, 解得 t1=1+22 (舍), t2=1-22
∴P(1-22,-2
【双解】
解2° (2°表示情况2，这是通用的数学语言)
点K位于线段OE上时, 延长SK交 AE于T, 交AP于M。同理, 有△ADE≌△BDF(SAS)
∴∠DBF=∠DAE,又∵∠DBF+∠DBT=180° ∴∠DBT+∠DAE=180°
∴∠ATB=(4-2)×180°-∠ADB-(∠TAD+∠OBT)=360°-90° -180° =90°
∵∠APB+∠PBK=∠PAE, ∠AMB=∠APB+∠MBP
∴∠AMT=∠MAT,∴∠AMT=∠MAT=1/2∠ATB=1/2×90° =45°
作 PS⊥AP 交 AE 延长线于S, 则 ∠APS=90°,
第11页,共12页 ∠ASP=180°-∠APS-∠PAS=180°-90°-45°=45°
∴∠PAS=∠ASP=45° ∴AP=PS
作 PR⊥AB于R, SH⊥PR于H, 交y轴于N。
则 ∠ARP=∠H=90°
∴∠ARP= ∠APS
∴∠RAP=∠HRA-∠PRA=∠HPA-∠APS=∠HPS
又∵AP=SP,∴△APR∽△PSH(AAS)
∴PH=AR,SH=PR
P=t-12t2+t+32,则 PR=12t2-t-32,0R=-t
∴PH=AR=0R-0A=-t-1……
SH=PR=12t2-t-32
又∵∠H=∠PRO= ∠RON=90°
∴四边形 RONH是矩形
∴ON=RH=PR+PH=12t2-t-32+-t-1
5 . =12t2-2t-52
∴HN=OR=-t
SN=SH-NH=12t2-t-32--t=12t2-32
则1°可知,
OE=-32-32t
EN=0N-OE=12t2-2t-52--32-32t)· 1 · · · 2
=12t2-12t-11 ^1
∴∠ENS=∠EOA=90°,∠NES=OEA
∴△OEA∽ △NES
注意：因借用原卷的图，所以图中角度不准，图中用紫 色标记的角ATM是90度直角。 ∴OENE=OASN 即 -32-32t12t2-12t-1=112t2-32
即: -32t+112t-2t+1=112t2-3
∵t+1≠0,
原式， 即 -32t-2=1t2-3 解得， t1=-13+2310,t2=-13-2310
P-13-2210-12-13-23102+-13-2310+17
即 P-13-2310-109-8109,
综上所述 P11-22-2或 P2-13-2103-109-8109
第12页,共12页