初中数学12.3 角的平分线的性质说课课件ppt

这是一份初中数学12.3 角的平分线的性质说课课件ppt，共22页。PPT课件主要包含了度量法，折叠法，角平分仪，ADAB，ACAC，DCBC，角平分仪模型，四边形ABCD，ABAD，CBCD等内容，欢迎下载使用。
通过折纸，你能折出角平分线吗？
一、折纸活动，引出新知
你还有什么方法作一个角的角平分线？
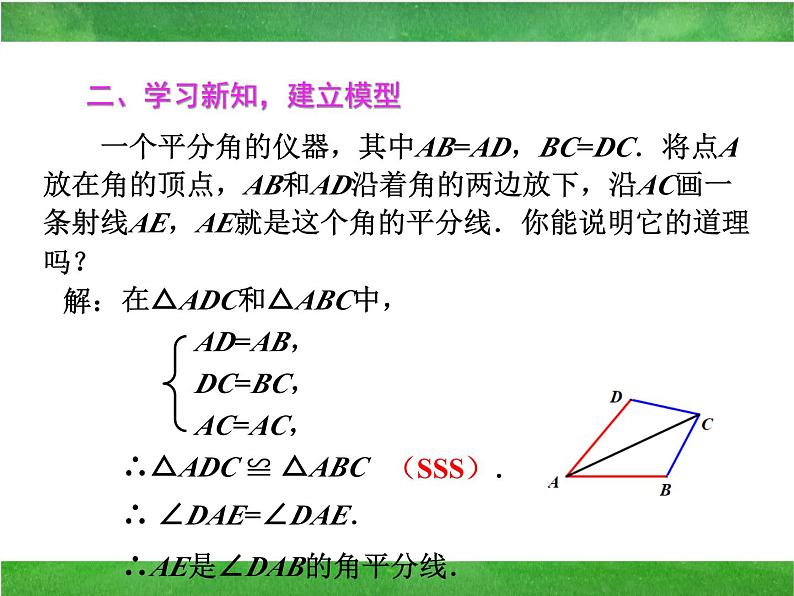
在△ADC和△ABC中，
∴△ADC ≌ △ABC
∴ ∠DAE=∠DAE．
∴AE是∠DAB的角平分线．
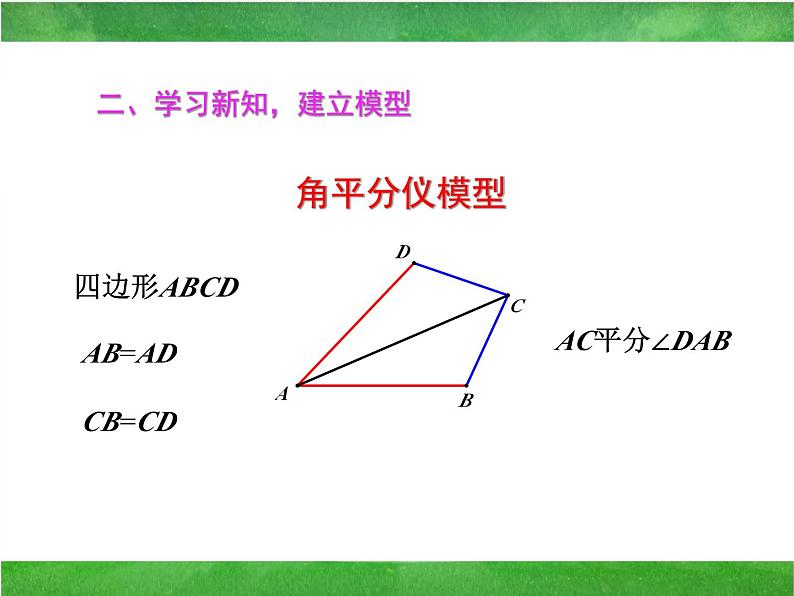
　　一个平分角的仪器，其中AB=AD，BC=DC．将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是这个角的平分线．你能说明它的道理吗？
二、学习新知，建立模型
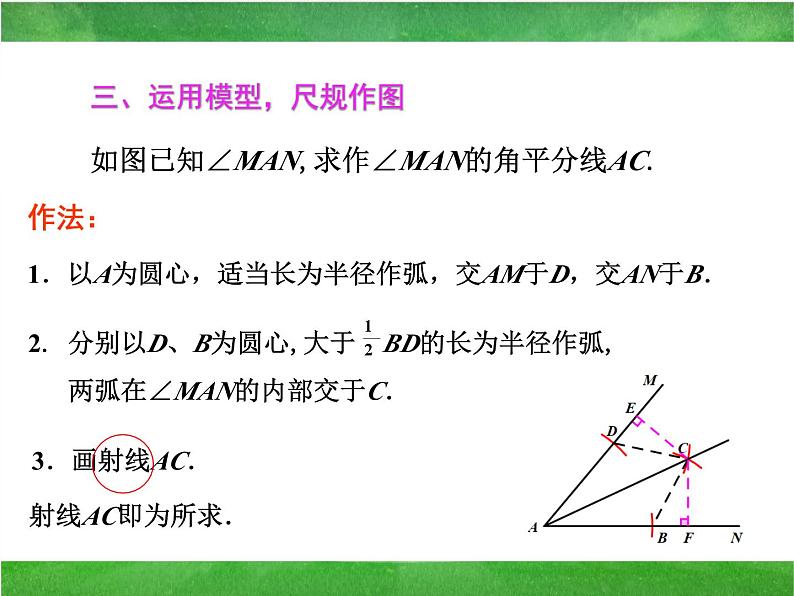
　1．以A为圆心，适当长为半径作弧，交AM于D，交AN于B．
如图已知∠MAN,求作∠MAN的角平分线AC.
三、运用模型，尺规作图
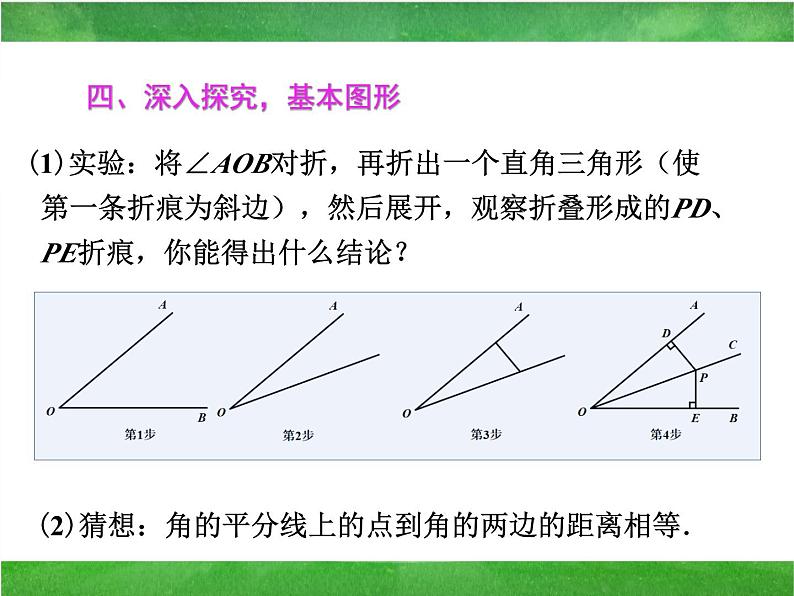
(1)实验：将∠AOB对折，再折出一个直角三角形（使第一条折痕为斜边），然后展开，观察折叠形成的PD、PE折痕，你能得出什么结论？
四、深入探究，基本图形
(2)猜想：角的平分线上的点到角的两边的距离相等．
证明：∵ OC 平分∠AOB ， ∴ ∠1=∠2． ∵ PD⊥OA，PE⊥OB， ∴ ∠PDO=∠PEO． 在△PDO和△PEO中， ∠PDO=∠PEO， ∠1=∠2， OP =OP ，
如图，OC 平分∠AOB，点P在OC上，PD⊥OA于点D，PE⊥OB于点E，求证：PD =PE.
∴ △PDO ≌ △PEO（AAS）． ∴ PD =PE．
　　一般情况下，我们要证明一个几何命题时，会按照类似的步骤进行，即　　1．明确命题中的已知和求证；　　2．根据题意，画出图形，并用符号表示已知和求证；　　3．经过分析，找出由已知推出要证的结论的途径，　　　写出证明过程.
角的平分线上的点到角的两边的距离相等
∵ ∠1=∠2 PD⊥OA PE⊥OB∴ PD=PE
OC平分∠AOB PD⊥OA PE⊥OB
角平分线性质的基本图形
　　例　如图，△ABC中，BC=8，BD=5，∠C=90°，AD为∠CAB的平分线，DE⊥AB，则DE为 .
五、变式训练，强化新知
变式1　如图，△ABC中，BC=8，BD=5，∠C=90°，AD为∠CAB的平分线，点P在AB上运动，则DP的最小值为 .
变式2　如图，△ABF中，DC=3，AB=8，AD为∠CAB的平分线， DC⊥AF， 则△ABD的面积为 .
过角平分线上的点作角边上的垂线段
　　变式3　如图，△ABF中，AB=AF, AD为∠CAB的平分线，DC⊥AF, DE⊥AB，求证：CF＝BE．
∵ AD平分∠CAB，DC⊥AF, DE⊥AB,∴ CD=ED, ∠DCA=∠DEA=90°．在Rt△ACD和Rt△AED中， CD=ED， AD=AD，∴ Rt△ACD≌Rt△AED(HL）．∴ AC=AE．∵ AF=AB，∴ CF=BE．
△DBE　　△DFC　　
变式4　△ABF中，AB=AF, AD为∠CAB的平分线，DC⊥AF, DE⊥AB,如图所示，将△FCD沿CD折叠.
（1）DF'　　DB （2）∠DF'C　　∠B （3）∠DF'A+∠B=　　　°
△DBE≌△DFC≌△DF'C
　　变式5　如图，四边形ABCD中，AC平分∠BAD，CD=CB．求证：∠B+∠ADC=180°.
过点C作CE⊥AB于点E，CF⊥AD交于点F，∵ AC平分∠BAD，CE⊥AB，CF⊥AD，∴ CF=CE，∠CFD=∠CEB=90°.在Rt△CFD和Rt△CEB中 CF=CE， CD=DB，∴ Rt△CFD≌Rt△CEB（HL）.∴ ∠CDF=∠B.∵ ∠CDF+∠ADC=180°，∴ ∠B+∠ADC=180°.
六、反思归纳，梳理提炼
角的平分线的性质：角的平分线上的点到角两边的距离相等
(一)基础强化（必做）
七、布置作业，提升能力
1．如图，AD 是△ABC的角平分线，若∠B=90°，BD=4 ，则点D到AC 的距离是（    ） A．2 B．3 C．4 D．5
2．如图，点D是BC上一点，AD平分∠BAC，AB＝5，AC＝4，若 S△ABD＝m ，则S△ADC＝_____（用m的代数式表示）．
3．如图，在△ABC中，AD是它的角平分线，且BC=CD，DE⊥AC，DF⊥AB，垂足分别为E，F．求证：BF=CE．
六、布置作业，提升能力
4．如图，在△ABC中，∠C=90°，∠CAD=∠BAD，DE⊥AB于E，点 F在边AC上．（1）求证：DC=DE；（2）若AC=4，AB=5，且△ABC的面积等于6，　　 求DE的长．
(二)能力提升（必做）
5．如图，已知AC平分∠BAD，CE⊥AB于E 点，∠ADC+∠CBE=180°． 求证：（1）BC=CD； （2）AB+AD=2AE．
(三)素养闯关（选做）