2023-2024学年甘肃省兰州一中七年级（上）期末数学试卷(含详细答案解析)

这是一份2023-2024学年甘肃省兰州一中七年级（上）期末数学试卷(含详细答案解析)，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.用科学记数法表示0.000059，正确的是( )
A. 5.9×10−5B. 5.9×10−4C. 0.59×10−3D. 0.59×10−4
2.下列说法中，正确的是( )
A. 单项式−3x2y的系数是3，次数是3B. 单项式x的系数是0，次数是1
C. 3(xy+2)是二次单项式D. 单项式−13xy2的系数是−13，次数是3
3.下列选项中，左边的平面图形能够折成右边封闭的立体图形的是( )
A. B.
C. D.
4.下列不能用平方差公式运算的是( )
A. (−x+2)(−x−2)B. (−2m−n)(−2m−n)
C. (−2a+b)(2a+b)D. (y−x)(−x−y)
5.如图，方格纸上每个小正方形的边长都相同，若使阴影部分能折叠成一个正方体，则需剪掉一个小正方形，剪掉的小正方形不可以是( )
A. ④B. ③C. ②D. ①
6.下列说法中正确的个数是( )
①无交点的两直线平行；
②相等的角是对顶角；
③两条直线被第三条直线所截，所得的同位角相等；
④两条平行线被第三条直线所截，一对内错角的角平分线互相平行.
A. 4B. 3C. 2D. 1
7.解方程：x2−x−26=1−x−13，下面去分母变形正确的是( )
A. 3x−(x−2)=6−2(x−1)B. 3x−x−2=6−2(x−1)
C. 3x−(x+2)=1−2(x−1)D. 3x−x+2=3−2(x−1)
8.已知2a=5，4b=7，则2a+2b的值是( )
A. 35B. 19C. 12D. 10
9.把一副三角板放在水平桌面上，摆放成如图所示形状，若DE//AB，则∠1的度数为( )
A. 105∘
B. 115∘
C. 120∘
D. 135∘
10.如图所示的运算程序中，如果开始输入的x值为−48，我们发现第1次输出的结果为−24，第2次输出的结果为−12，…，第2024次输出的结果为( )
A. −6B. −3C. −24D. −12
11.已知9y2−my+4是完全平方式，则m的值为( )
A. 6B. ±6C. 12D. ±12
12.某同学晚上6点多钟开始做作业，他家墙上时钟的时针和分针的夹角是120∘，他做完作业后还是6点多钟，且时针和分针的夹角还是120∘，此同学做作业大约用了( )
A. 40分钟B. 42分钟C. 44分钟D. 46分钟
二、填空题：本题共4小题，每小题3分，共12分。
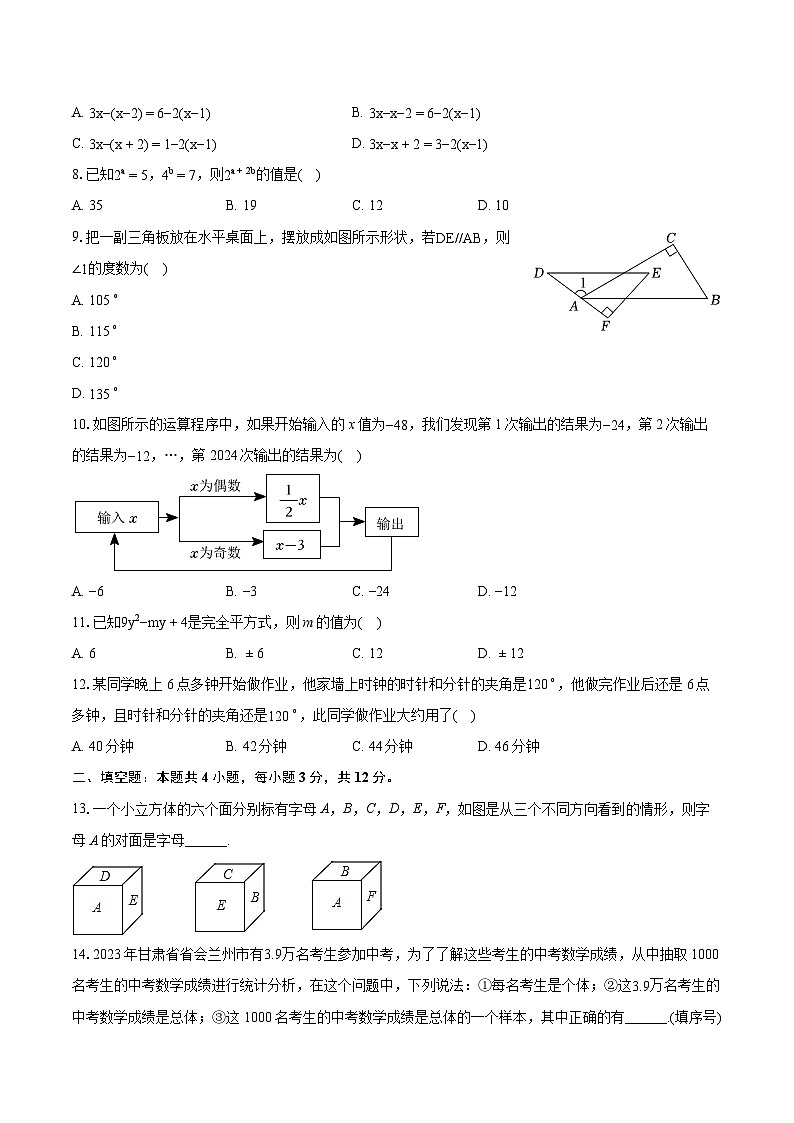
13.一个小立方体的六个面分别标有字母A，B，C，D，E，F，如图是从三个不同方向看到的情形，则字母A的对面是字母______.
14.2023年甘肃省省会兰州市有3.9万名考生参加中考，为了了解这些考生的中考数学成绩，从中抽取1000名考生的中考数学成绩进行统计分析，在这个问题中，下列说法：①每名考生是个体；②这3.9万名考生的中考数学成绩是总体；③这1000名考生的中考数学成绩是总体的一个样本，其中正确的有______.(填序号)
15.已知t+1t=3，则3t9+t2+13t5=______.
16.将一副直角三角板如图1摆放在直线MN上(直角三角板ABC和直角三角板EDC，∠EDC=90∘，∠DEC=60∘，∠ABC=90∘，∠BAC=45∘)，保持三角板EDC不动，将三角板ABC绕点C以每秒5∘的速度顺时针旋转，旋转时间为t秒，当AC与射线CN重合时停止旋转.在旋转过程中，当三角板ABC的AB边平行于三角板EDC的某一边时(不包含重合的情形)，此时t的值为______.
三、解答题：本题共12小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题4分)
计算：(−2)2+4×(−1)2022+(−12)−3+(π−5)0.
18.(本小题4分)
先化简，再求值：
(a−b)2−2a(a+3b)+(a+2b)(a−2b)，其中a=1，b=−3.
19.(本小题4分)
已知(x+y)2=25，(x−y)2=9，求xy与x2+y2的值.
20.(本小题8分)
如图是由棱长都为1cm的6块小正方体组成的简单几何体．
(1)请在方格中画出该几何体的三个视图．
(2)如果在这个几何体上再添加一些小正方体，并保持主视图和左视图不变，最多可以再添加______块小正方体，
21.(本小题4分)
小亮的一张地图上有A、B、C三个城市，但地图上的C城市被墨迹污染了(如图)，但知道∠BAC=∠1，∠ABC=∠2，请你用尺规作图法帮他在如图中确定C城市的具体位置．(用尺规作图，保留作图痕迹，不写作法)
22.(本小题6分)
以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生，现随机调查了m名新聘毕业生的专业情况，并将调查结果绘制成如图两幅不完整的统计图.
请根据统计图提供的信息，解答下列问题.
(1)m=______，n=______.
(2)请补全条形统计图；
(3)若该公司新招聘600名毕业生，请你估计“总线”专业的毕业生有______名.
23.(本小题6分)
列方程解应用题：
某车间每天能生产甲种零件180个或乙种零件120个，若甲、乙两种零件分别取3个、2个配成一套，那么要在30天内生产最多的成套产品，应怎样安排生产甲、乙两种零件的天数？
24.(本小题6分)
如图所示，在数轴上原点O表示数0，A点在原点的左侧，所表示的数是a；B点在原点的右侧，所表示的数是b，并且a、b满足|a+8|+|b−4|=0.
(1)点A表示的数为______，点 B表示的数为______；
(2)若点P从点A出发沿数轴向右运动，速度为每秒3个单位长度；点Q从点B出发沿数轴向左运动，速度为每秒1个单位长度，P、Q两点同时运动，在P、Q运动的过程中，当P、Q两点的距离为2个单位长度时，求点Q表示的数.
25.(本小题8分)
如果两个方程的解相差1，则称解较大的方程为另一个方程的“后移方程”．例如：方程x−2=0是方程x−1=0的后移方程．
(1)判断方程2x+1=0是否为方程2x+3=0的后移方程______(填“是”或“否”)；
(2)若关于x的方程3x+m+n=0是关于x的方程3x+m=0的后移方程，求n的值．
(3)当a≠0时，如果方程ax+b=0是方程ax+c=0的后移方程，用等式表达a，b，c满足的数量关系______.
26.(本小题8分)
如图，正方形ABCD的边长为a，点E在AB边上，四边形EFGB也是正方形，它的边长为b(a>b)，连接AF、CF、AC.
(1)用含a、b的代数式表示GC=______；
(2)若两个正方形的面积之和为60，即a2+b2=60，又ab=20，图中线段GC的长；
(3)若a=8，△AFC的面积为S，则S=______.
27.(本小题4分)
是否存在一个三位数abc−(a,b,c取从1到9的自然数)，使得abc−+bca−+cab−为完全平方数？
28.(本小题10分)
如图1，直角三角板ABC(∠ABC=30∘)的直角边AC所在直线与直线MN重合.将该三角板绕点A逆时针旋转一定角度后，如图2所示.记∠CAN=∠α(0∘