2023-2024学年新疆乌鲁木齐市七年级（上）期末数学试卷(含详细答案解析)

这是一份2023-2024学年新疆乌鲁木齐市七年级（上）期末数学试卷(含详细答案解析)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.在−1，0，1，1.5这四个数中，负数是( )
A. −1B. 0C. 1D. 1.5
2.2023年5月30日上午，我国载人航天飞船“神舟十六号”发射圆满成功，与此同时，中国载人航天办公室也宣布计划在2030年前实现中国人首次登陆距地球平均距离为384000千米的月球，将384000用科学记数法表示为( )
A. 0.384×106B. 38.4×104C. 3.84×10−5D. 3.84×105
3.单项式−9x2y3的系数和次数分别是( )
A. 系数是9，次数是5B. 系数是9，次数是6
C. 系数是−9，次数是5D. 系数是−9，次数是6
4.如图，是一个正方体的表面展开图，则原正方体中“梦”字所在的面相对的面上标的字是( )
A. 伟
B. 大
C. 的
D. 国
5.下列说法不一定正确的是( )
A. 若2a=6，则a=3B. 若a−3=b−3，则a=b
C. 若a=b，则−2a=−2bD. 若ac=bc，则a=b
6.下面四个整式中，不能表示图中阴影部分面积的是( )
A. x2+5xB. x(x+3)+6
C. 3(x+2)+x2D. (x+3)(x+2)−2x
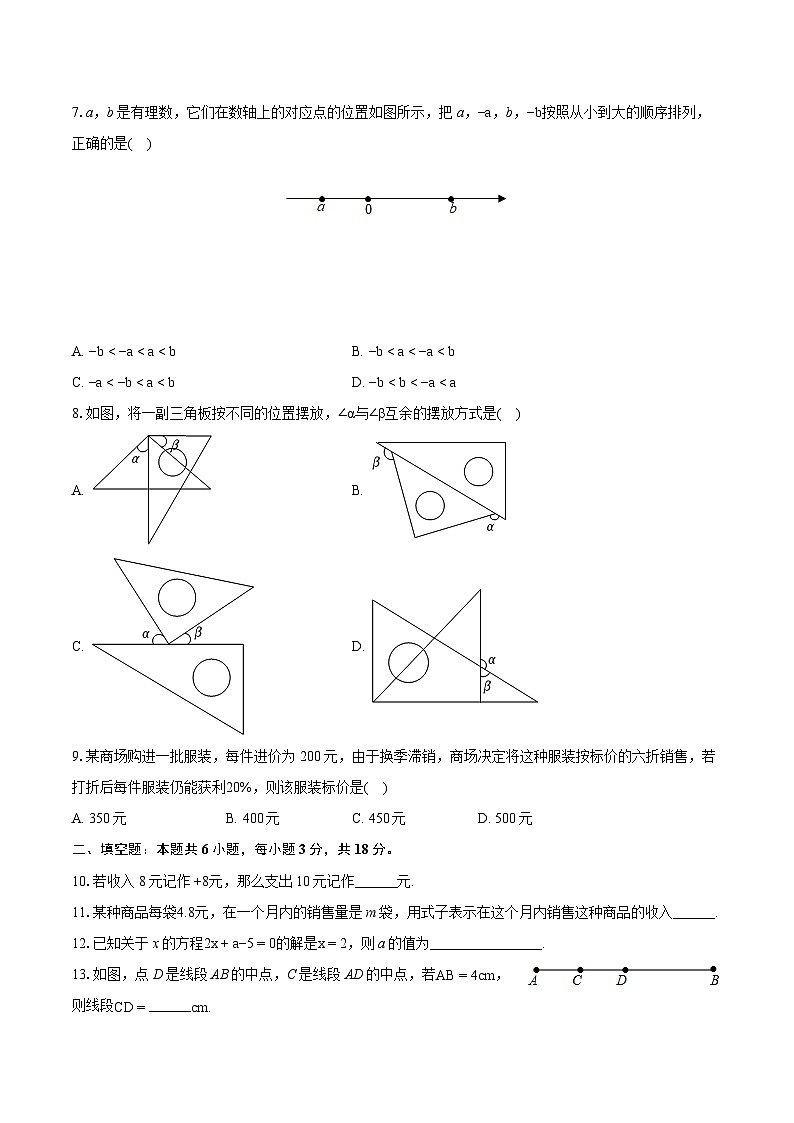
7.a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，−a，b，−b按照从小到大的顺序排列，正确的是( )
A. −b<−aC. −a<−b8.如图，将一副三角板按不同的位置摆放，∠α与∠β互余的摆放方式是( )
A. B.
C. D.
9.某商场购进一批服装，每件进价为200元，由于换季滞销，商场决定将这种服装按标价的六折销售，若打折后每件服装仍能获利20%，则该服装标价是( )
A. 350元B. 400元C. 450元D. 500元
二、填空题：本题共6小题，每小题3分，共18分。
10.若收入8元记作+8元，那么支出10元记作______元.
11.某种商品每袋4.8元，在一个月内的销售量是m袋，用式子表示在这个月内销售这种商品的收入______.
12.已知关于x的方程2x+a−5=0的解是x=2，则a的值为________________.
13.如图，点D是线段AB的中点，C是线段AD的中点，若AB=4cm，则线段CD=______cm.
14.若有理数a，b满足|a+3|+(b−2)2=0，则ab的值为______.
15.一架飞机从A机场顺风飞到B机场要用2.8小时，逆风飞行同样的航线要用3小时，这架飞机无风时从A机场飞到B机场大约用______小时(结果精确到0.01).
三、解答题：本题共7小题，共55分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题12分)
计算下列各题：
(1)3−4+11；
(2)3×(−4)+(−28)+7；
(3)(−2)3−(−3)×(−12+2).
17.(本小题6分)
先化简，再求值：2x2−5x+x2+4x−3x2+3，其中x=2.
18.(本小题10分)
解方程：
(1)2x−1=3；
(2)2x+12−1=x−34.
19.(本小题7分)
根据下列语句，画出图形．
已知四点A、B、C、D.
①画直线AB；
②连接AC、BD，相交于点O；
③画射线AD、BC，交于点P.
20.(本小题6分)
某工厂的产值连续增长，去年是前年的1.5倍，今年是去年的2倍，这三年总产值为550万元．前年的产值是多少？
21.(本小题6分)
如图，点O在直线AB上，已知∠COD=90∘，∠AOC=30∘，且OE平分∠BOC，求∠DOE.
22.(本小题8分)
为鼓励居民节约用电、某地试行分档收费，具体执行方案如表：
例如：一户居民七月份用了400度电，则需缴电费400×0.85=340(元)
请根据以上信息完成下列问题：
(1)若某居民四月份缴电费180元，则该用户四月份用了______度电.
(2)若某居民五、六月份共用电500度，缴电费290.5元.已知该用户六月份用电量大于五月份.问该户居民五、六月份各用电多少度？
答案和解析
1.【答案】A
【解析】解：在−1，0，1，1.5这四个数中，负数是−1，
故选：A.
利用正数负数的定义判断即可．
本题考查了正数负数，解题的关键是掌握正数负数的定义．
2.【答案】D
【解析】解：384000=3.84×105，
故选：D.
根据科学记数法的表示方法求解即可．
本题主要考查科学记数法．科学记数法的表示形式为a×10n的形式，其中1≤a<10，n为整数．解题关键是正确确定a的值以及n的值．
3.【答案】C
【解析】解：单项式−9x2y3的系数是−9，次数分是2+3=5.
故选：C.
根据单项式系数及次数的定义解答即可．
本题考查的是单项式，熟知单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数是解题的关键．
4.【答案】A
【解析】解：这是一个正方体的平面展开图，共有六个面，其中面“梦”与面“伟”相对，面“大”与面“中”相对，面“国”与面“的”相对．
故选A.
利用正方体及其表面展开图的特点解题．
本题考查了正方体相对面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．
5.【答案】D
【解析】解：A.2a=6，
等式两边都除以2，得a=3，故本选项不符合题意；
B.a−3=b−3，
等式两边都加3，得a=b，故本选项不符合题意；
C.a=b，
等式两边都乘−2，得−2a=−2b，故本选项不符合题意；
D.当c=0时，由ac=bc不能推出a=b，故本选项符合题意．
故选：D.
根据等式的性质逐个判断即可．
本题考查了等式的性质，能正确根据等式的性质进行变形是解此题的关键．
6.【答案】A
【解析】【分析】
本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．
根据图形，可以用代数式表示出图中阴影部分的面积，本题得以解决．
【解答】
解：由图可得，
图中阴影部分的面积为：x2+3x+2×3=x2+3x+6，故选项A符合题意，
x(x+3)+2×3=x(x+3)+6=x2+3x+6，故选项B不符合题意，
3(x+2)+x2=x2+3x+6，故选项C不符合题意，
(x+3)(x+2)−2x=x2+3x+6，故选项D不符合题意，
故选：A.
7.【答案】B
【解析】【分析】
此题主要考查了有理数的大小比较的方法，以及数轴的特征．根据图示，可得：a<0【解答】
解：因为a<0所以0<−a所以−b故选：B.
8.【答案】C
【解析】解：A.∠α=∠β，故A选项不符合题意；
B.∠α+∠β=270∘，故B选项不符合题意；
C.∠α+∠β=90∘，故C选项符合题意；
D..∠α+∠β=180∘，故D选项不符合题意．
故选：C.
求每个图中∠α与∠β的数量关系．
本意主要考查余角和补角的定义，解决本题的关键是熟练运用这些知识点解决两角之间的数量关系．
9.【答案】B
【解析】【分析】
本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程．
设该服装标价为x元，根据售价-进价=利润列出方程，解出即可．
【解答】
解：设该服装标价为x元，
由题意，得0.6x−200=200×20%，
解得：x=400.
故选：B.
10.【答案】−10
【解析】解：如果收入8元记作+8元，那么支出10元记作：−10元．
故答案为：−10.
本题收入记住“+”，则支出记作“-”，据此即可求解．
本题考查了正负数在实际生活中的应用，解题的关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．
11.【答案】4.8m
【解析】解：这个月内销售这种商品的收入4.8m，
故答案为：4.8m.
根据销售这种商品的收入等于数量与单价乘积列出代数式即可．
本题考查了列代数式的知识，解题的关键是销售这种商品的收入等于数量与单价乘积关系式．
12.【答案】1
【解析】解：把x=2代入方程，得：4+a−5=0，
解得：a=1.
故答案是：1.
把x=2代入方程即可得到一个关于a的方程，解方程即可求解.
本题考查了方程的解的定义，理解定义是关键．
13.【答案】1
【解析】解：∵点D是线段AB的中点，AB=4cm，
∴AD=12AB=12×4=2(cm)，
∵C是线段AD的中点，
∴CD=12AD=12×2=1(cm).
答：线段CD的长度是1cm.
故答案为：1.
先根据点D是线段AB的中点求出AD的长，再由由点C是线段AD的中点求出CD的长即可．
本题考查的是两点间的距离，熟知各线段之间的倍数关系是解答此题的关键．
14.【答案】−6
【解析】解：∵|a+3|≥0，(b−2)2≥0，
并且|a+3|+(b−2)2=0，
∴|a+3|=0，(b−2)2=0，
∴a+3=0，b−2=0，
∴a=−3，b=2，
∴ab=−6.
故答案为：−6.
根据绝对值和完全平方的非负性先求出a、b的值，再求出ab的值．
本题考查了绝对值和完全平方的非负性，掌握几个非负数的和等于0，则每个非负数都为0这个性质是解题的关键
15.【答案】2.89
【解析】解：设这架飞机无风时从A机场飞到B机场大约用x小时，
则12(13+12.8)x=1，
解得：x≈2.89，
故答案为：2.89.
根据“路程=时间×速度”列方程求解．
本题考查了一元一次方程的应用，找到相等关系是解题的关键．
16.【答案】解：(1)3−4+11
=−1+11
=10；
(2)3×(−4)+(−28)+7
=−12−28+7
=−40+7
=−33；
(3)(−2)3−(−3)×(−12+2)
=−8−(−3)×(−1+2)
=−8−(−3)×1
=−8+3
=−5.
【解析】(1)按照从左到右的顺序进行计算，即可解答；
(2)先算乘法，后算加减，即可解答；
(3)先算乘方，再算乘法，后算加减，有括号先算括号里，即可解答；
本题考查了有理数的混合运算，准确熟练地进行计算是解题的关键．
17.【答案】解：原式=(2+1−3)⋅x2+(−5+4)⋅x+3
=−x+3.
当x=2时，原式=−2+3=1.
【解析】根据合并同类项法则：合并同类项后，所得项的系数是合并前各同类项的系数之和，且字母连同它的指数不变，可得最简结果，再将x的值代入计算即可．
本题考查整式的加减-化简求值，熟练掌握运算法则是解答本题的关键．
18.【答案】解：(1)2x−1=3，
移项，得2x=3+1，
合并同类项，得2x=4，
系数化成1，得x=2；
(2)2x+12−1=x−34，
去分母，得2(2x+1)−4=x−3，
去括号，得4x+2−4=x−3，
移项，得4x−x=−3−2+4，
合并同类项，得3x=−1，
系数化成1，得x=−13.
【解析】(1)移项，合并同类项，系数化成1即可；
(2)去分母，去括号，移项，合并同类项，系数化成1即可．
本题考查了解一元一次方程，能正确根据等式的性质进行变形是解此题的关键．
19.【答案】解：如图所示．

【解析】根据直线、线段和射线的定义作出即可．
本题考查了直线、射线、线段，主要是对文字语言转化为图形语言的能力的培养．
20.【答案】解：设前年的产值是x万元，由题意得
x+1.5x+1.5x×2=550，
解得：x=100.
答：前年的产值是100万元．
【解析】设前年的产值是x万元，根据题意可得去年的产值是1.5x万元，今年的产值是1.5x×2=3x万元，根据这三年的总产值为550万元，列出方程求解即可．
此题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出等量关系列出方程解决问题．
21.【答案】解：∵点O在直线AB上，∠AOC=30∘，
∴∠BOC=180∘−∠AOC=180∘−30∘=150∘，
∵OE平分∠BOC，
∴∠COE=12∠BOC=12×150∘=75∘，
∵∠COD=90∘，
∴∠DOE=∠COD−∠COE=90∘−75∘=15∘.
∴∠DOE的度数为15∘.
【解析】已知∠COD=90∘，要求∠DOE，求出∠COE的度数是关键，由于OE是∠BOC的角平分线，利用平角求出∠BOC即可．
本题考查角的计算，角的平分线的性质，平角，角的和差．读懂图学会分析是解题的关键．
22.【答案】300
【解析】解：(1)设该用户四月份用了x度电，
∵0.55×200=110(元)，0.6×400=240(元)，110<180<240，
∴200根据题意得：0.6x=180，
解得：x=300，
∴该用户四月份用了300度电．
故答案为：300；
(2)设该户居民五月份用电y度，则六月份用电(500−y)度，
当y≤100时，0.55y+0.85(500−y)=290.5，
解得：y=13453(不符合题意，舍去)；
当100解得：y=190，
∴500−y=500−190=310(度)；
当200答：该户居民五月份用电190度，六月份用电310度．
(1)设该用户四月份用了x度电，先求出用电量是200度及400度时需缴电费，将其与180元比较后可得出200(2)设该户居民五月份用电y度，则六月份用电(500−y)度，分y≤100，100本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．档次
每户每月用电数(度)
执行电价(元/度)
第一档
小于等于200
0.55
第二档
大于200小于400
0.6
第三档
大于等于400
0.85