第4章+三角形+单元测试卷（解析版）2023-2024学年北师大版数学七年级下册

这是一份第4章+三角形+单元测试卷（解析版）2023-2024学年北师大版数学七年级下册，共12页。

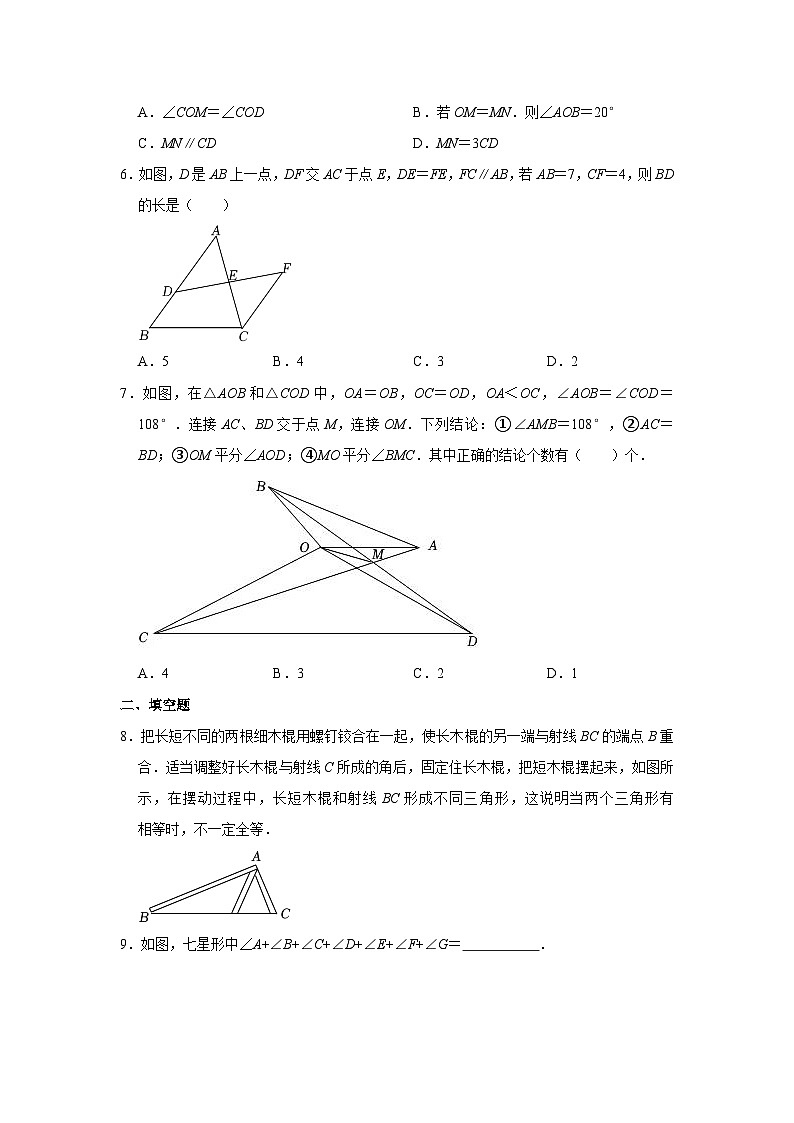
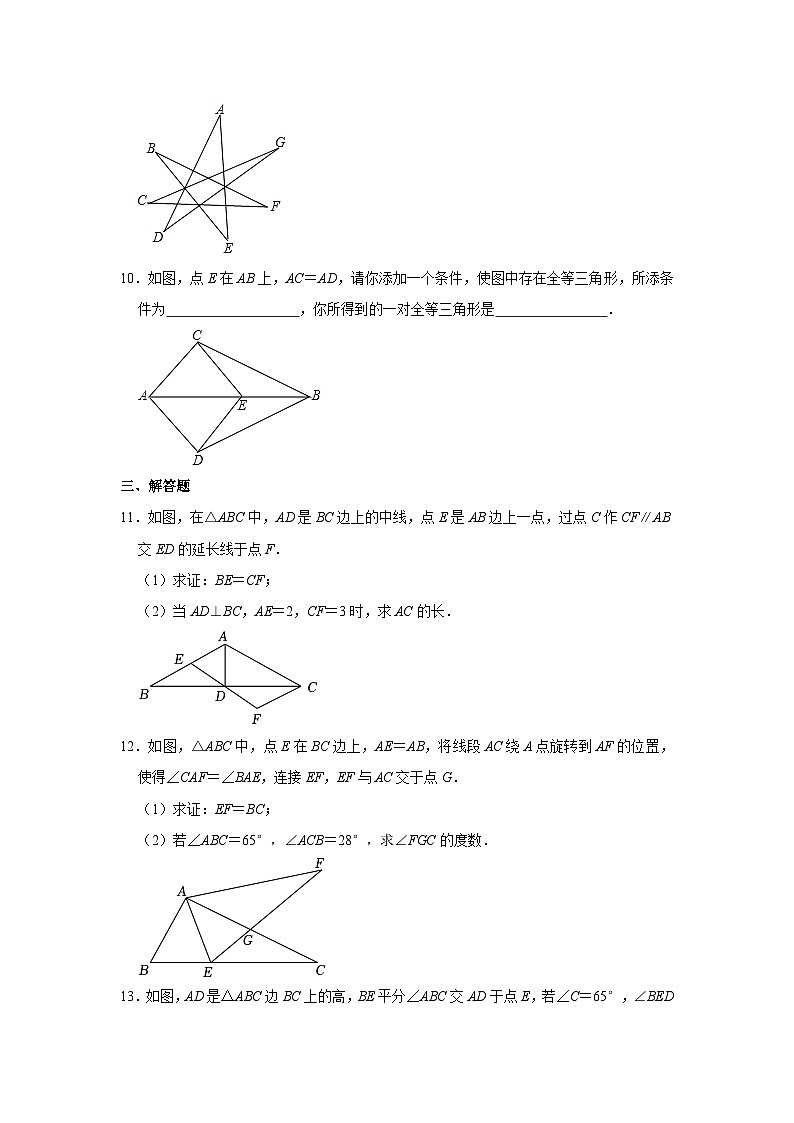
北师大新版七年级下册《第4章 复习课》练习一、选择题1．已知三角形的两边长分别为1和4，第三边长为整数，则该三角形的周长为（　　）A．7 B．8 C．9 D．102．已知n是正整数，若一个三角形的三边长分别是n+2，n+6，3n，则满足条件的n的值有（　　）A．4个 B．5个 C．6个 D．7个3．将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠α的度数是（　　）A．45° B．60° C．75° D．85°4．在△ABC中，若一个内角等于另外两个角的差，则（　　）A．必有一个角等于30° B．必有一个角等于45° C．必有一个角等于60° D．必有一个角等于90°5．已知锐角∠AOB，如图，（1）在射线OA上取一点C，以点O为圆心，OC长为半径作，交射线OB于点D，连接CD；（2）分别以点C，D为圆心，CD长为半径作弧，交于点M，N；（3）连接OM，MN．根据以上作图过程及所作图形，下列结论中错误的是（　　）A．∠COM＝∠COD B．若OM＝MN．则∠AOB＝20° C．MN∥CD D．MN＝3CD6．如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，若AB＝7，CF＝4，则BD的长是（　　）A．5 B．4 C．3 D．27．如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝108°．连接AC、BD交于点M，连接OM．下列结论：①∠AMB＝108°，②AC＝BD；③OM平分∠AOD；④MO平分∠BMC．其中正确的结论个数有（　　）个．A．4 B．3 C．2 D．1二、填空题8．把长短不同的两根细木棍用螺钉铰合在一起，使长木棍的另一端与射线BC的端点B重合．适当调整好长木棍与射线C所成的角后，固定住长木棍，把短木棍摆起来，如图所示，在摆动过程中，长短木棍和射线BC形成不同三角形，这说明当两个三角形有 　 　相等时，不一定全等．9．如图，七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G＝　 　．10．如图，点E在AB上，AC＝AD，请你添加一个条件，使图中存在全等三角形，所添条件为　 　，你所得到的一对全等三角形是　 　．三、解答题11．如图，在△ABC中，AD是BC边上的中线，点E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．（1）求证：BE＝CF；（2）当AD⊥BC，AE＝2，CF＝3时，求AC的长．12．如图，△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G．（1）求证：EF＝BC；（2）若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．13．如图，AD是△ABC边BC上的高，BE平分∠ABC交AD于点E，若∠C＝65°，∠BED＝68°，求∠ABC和∠BAC的度数．14．已知四边形ABCD中，AB＝AD，AB⊥AD，连接AC，过点A作AE⊥AC，且使AE＝AC，连接BE，过A作AH⊥CD于H交BE于F．（1）如图1，当E在CD的延长线上时，求证：①△ABC≌△ADE；②BF＝EF；（2）如图2，当E不在CD的延长线上时，BF＝EF还成立吗？请证明你的结论．15．两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC．（1）请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）；（2）证明：DC⊥BE．参考答案与试题解析一、选择题1．【解答】解：设第三边为x，根据三角形的三边关系，得：4﹣1＜x＜4+1，即3＜x＜5，∵x为整数，∴x的值为4． 三角形的周长为1+4+4＝9．故选：C．2．【解答】解：①若n+2＜n+6≤3n，则，解得：3≤n＜8，∴正整数n有5个：3，4，5，6，7；②若n+2≤3n≤n+6，则，解得：＜n≤3，∴正整数n有2个：2和3；综上所述，满足条件的n的值有6个，故选：C．3．【解答】解：如图，∵∠ACD＝90°、∠F＝45°，∴∠CGF＝∠DGB＝45°，则∠α＝∠D+∠DGB＝30°+45°＝75°，故选：C．4．【解答】解：∵∠A+∠B+∠C＝180°，∠A＝∠C﹣∠B，∴2∠C＝180°，∴∠C＝90°，∴△ABC是直角三角形，故选：D．5．【解答】解：由作图知CM＝CD＝DN，∴∠COM＝∠COD，故A选项正确；∵OM＝ON＝MN，∴△OMN是等边三角形，∴∠MON＝60°，∵CM＝CD＝DN，∴∠MOA＝∠AOB＝∠BON＝∠MON＝20°，故B选项正确；设∠MOA＝∠AOB＝∠BON＝α，则∠OCD＝∠OCM＝，∴∠MCD＝180°﹣α，又∵∠CMN＝∠CON＝α，∴∠MCD+∠CMN＝180°，∴MN∥CD，故C选项正确；∵MC+CD+DN＞MN，且CM＝CD＝DN，∴3CD＞MN，故D选项错误；故选：D．6．【解答】解：∵CF∥AB，∴∠A＝∠FCE，∠ADE＝∠F，在△ADE和△FCE中，，∴△ADE≌△CFE（AAS），∴AD＝CF＝4，∵AB＝7，∴DB＝AB﹣AD＝7﹣4＝3．故选：C．7．【解答】解：∵∠AOB＝∠COD＝108°，∴∠AOB+∠AOD＝∠COD+∠AOD，即∠AOC＝∠BOD，在△AOC和△BOD中，，∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，故②正确；∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OAC＝∠AOB+∠OBD，∴∠AMB＝∠AOB＝108°，故①正确；作OG⊥AC于G，OH⊥BD于H，如图所示，则∠OGA＝∠OHB＝90°，∵△AOC≌△BOD，∴OG＝OH，∴MO平分∠BMC，故④正确；∴∠BMO＝∠CMO，∵∠AMB＝∠DMC，∴∠AMO＝∠DMO，假设OM平分∠AOD，则∠AOM＝∠DOM，在△AMO与△DMO中，，∴△AMO≌△DMO（ASA），∴AO＝OD，∵OC＝OD，∴OA＝OC，而OA＜OC，故③错误；所以其中正确的结论是①②④，共3个．故选：B．二、填空题8．【解答】解：如图所示，在摆动过程中，长短木棍和射线BC形成不同三角形，这说明当两个三角形有两边对应相等且其中一组对应边所对的角相等时，这两个三角形不一定全等．故答案为：两边对应相等且其中一组对应边所对的角．9．【解答】解：由三角形的外角性质得，∠1＝∠B+∠F+∠C+∠G，∠2＝∠A+∠D，由三角形的内角和定理得，∠1+∠2+∠E＝180°，所以，∠A+∠B+∠C+∠D+∠E+∠F+∠G＝180°．故答案为：180°．10．【解答】解：如果添加CE＝DE，∵AC＝AD，AE＝AE，∴△ACE≌△ADE（SSS）本题有其它添加条件的方法．故填CE＝DE（答案不唯一），△ACE≌△ADE．三、解答题11．【解答】（1）证明：∵CF∥AB，∴∠B＝∠FCD，∠BED＝∠F，∵AD是BC边上的中线，∴BD＝CD，在△BDE和△CDF中，，∴△BDE≌△CDF（AAS），∴BE＝CF；（2）解：∵△BDE≌△CDF，∴BE＝CF＝3，∴AB＝AE+BE＝2+3＝5，∵AD⊥BC，BD＝CD，∴AC＝AB＝5．12．【解答】（1）证明：∵∠CAF＝∠BAE，∴∠BAC＝∠EAF．∵将线段AC绕A点旋转到AF的位置，∴AC＝AF．在△ABC与△AEF中，，∴△ABC≌△AEF（SAS），∴EF＝BC；（2）解：∵AB＝AE，∠ABC＝65°，∴∠BAE＝180°﹣65°×2＝50°，∴∠FAG＝∠BAE＝50°．∵△ABC≌△AEF，∴∠F＝∠C＝28°，∴∠FGC＝∠FAG+∠F＝50°+28°＝78°．13．【解答】解：∵AD是BC边上的高，∴∠ADB＝∠ADC＝90°，∴∠BED+∠EBD＝90°，∵∠BED＝68°，∴∠EBD＝22°，∵BE平分∠ABC，∴∠ABC＝2∠EBD＝44°；∵∠ABC+∠BAC+∠C＝180°，∵∠C＝65°，∴∠BAC＝71°．14．【解答】证明：（1）①如图1，∵AB⊥AD，AE⊥AC，∴∠BAD＝90°，∠CAE＝90°，∴∠1＝∠2，在△ABC和△ADE中，∵，∴△ABC≌△ADE（SAS）；②如图1，∵△ABC≌△ADE，∴∠AEC＝∠3，在Rt△ACE中，∠ACE+∠AEC＝90°，∴∠BCE＝90°，∵AH⊥CD，AE＝AC，∴CH＝HE，∵∠AHE＝∠BCE＝90°，∴BC∥FH，∴＝＝1，∴BF＝EF；（2）结论仍然成立，理由是：如图2所示，过E作MN∥AH，交BA、CD延长线于M、N，∵∠CAE＝90°，∠BAD＝90°，∴∠1+∠2＝90°，∠1+∠CAD＝90°，∴∠2＝∠CAD，∵MN∥AH，∴∠3＝∠HAE，∵∠ACH+∠CAH＝90°，∠CAH+∠HAE＝90°，∴∠ACH＝∠HAE，∴∠3＝∠ACH，在△MAE和△DAC中，∵∴△MAE≌△DAC（ASA），∴AM＝AD，∵AB＝AD，∴AB＝AM，∵AF∥ME，∴＝＝1，∴BF＝EF．15．【解答】（1）△ABE≌△ACD．证明：∵△ABC与△AED均为等腰直角三角形，∴AB＝AC，AE＝AD，∠BAC＝∠EAD＝90°．∴∠BAC+∠CAE＝∠EAD+∠CAE．即∠BAE＝∠CAD，在△ABE与△ACD中，，∴△ABE≌△ACD；（2）证明∵△ABE≌△ACD，∴∠ACD＝∠ABE＝45°，又∵∠ACB＝45°，∴∠BCD＝∠ACB+∠ACD＝90°，∴DC⊥BE．