七年级上册3.4 一元一次方程模型的应用示范课ppt课件

这是一份七年级上册3.4 一元一次方程模型的应用示范课ppt课件，共10页。PPT课件主要包含了依题意得，3设未知数，2分析相等关系，1审题，4建立方程模型，5解方程，6检查解得合理性等内容，欢迎下载使用。
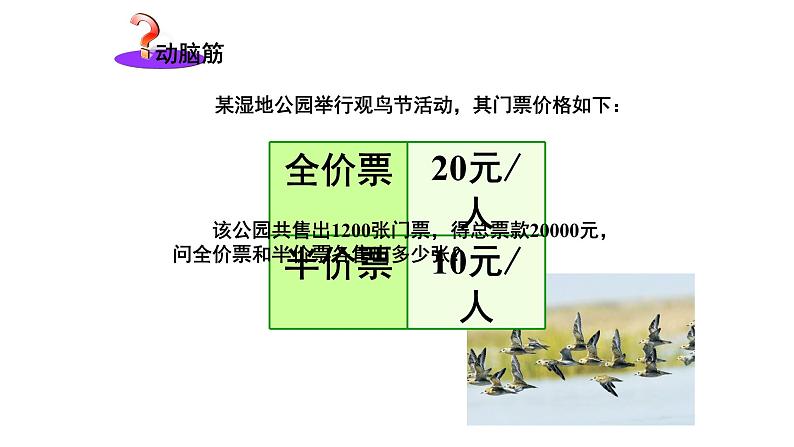
某湿地公园举行观鸟节活动，其门票价格如下：
该公园共售出1200张门票，得总票款20000元，问全价票和半价票各售出多少张？
解：设售出全价票x张，则售出半价票（1200-x）张,
x·20+(1200-x)·10=20000 .去括号，得20x+12000-10x=20000.移项，合并同类项，得10x=8000.即 x=800.半价票为 1200-800=400（张）.因此，全价票售出800张，半价票售出400张.
列一元一次方程解应用题的步骤有：
蕴含的相等关系.关键是要抓住题中关键的字、词、句加以分析，有时候还可借助图、表分析.
反复读题，想象实际问题的真实情景，
弄清其中各种数、量之间的关系.
在认真审题的前提下，找出题中
原方程的解，还要检查是否符合应用题的实际意义.
不但要检查方程的解是否为
例1 某房间里有四条腿的椅子和三条腿的凳子共16个， 如果椅子腿数与凳子腿数的和为60条，有几张椅子 和几条凳子？
分析 本问题中涉及的等量关系有： 椅子数+凳子数=16， 椅子腿数+凳子腿数=60.
解 设有x 张椅子，则有（16-x）条凳子.
根据题意，得4x+ 3(16-x)=60 .
去括号，得 4x+48-3x=60 .
移项，合并同类项，得 x = 12 .
凳子数为16-12=4（条）.
答：有12张椅子，4条凳子.
（1）解 设宽为xcm，则长为（5+x）cm.
根据题意，得2[x+ (5+x)]=60 .
去括号，得 2x+10+2x=60 .
移项，合并同类项，得 4x = 50.
系数化为1，得x=12.5.长为12.5+5=17.5（cm）.
答：长方形的长为17.5 cm.
1.（1）一个长方形的周长是60cm，且长比宽多5cm，求长方形的长；
解 设宽为2xcm，则长为3xcm.
根据题意，得2（2x+3x)=60 .
去括号，得 10x=60 .
系数化为1，得x=6.宽为2x=12（cm）.
答：长方形的宽为12 cm.
（2）一个长方形的周长是60cm，且长与宽的比是 3∶2，求长方形的宽.
2. 足球比赛的记分规则是：胜一场得3分，平一场 得1分，负一场得0分. 某队在某次比赛中共踢了 14场球，其中负5场，共得19分. 问这个队共胜了 多少场.
解 设这个队共胜了x场，则平了（9-x）场.
根据题意，得3x+（9-x)=19 .
去括号，得 3x+9-x=19.
移项，合并同类项，得 2x = 10.
系数化为1，得x=5.
答：这个队共胜了5场.