最新中考数学总复习真题探究与变式训练（讲义） 专题09 二次函数的图象与性质（6大考点）

这是一份最新中考数学总复习真题探究与变式训练（讲义） 专题09 二次函数的图象与性质（6大考点），文件包含专题09二次函数的图象与性质6大考点原卷版docx、专题09二次函数的图象与性质6大考点解析版docx等2份试卷配套教学资源，其中试卷共111页， 欢迎下载使用。
一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。
第三部分 函数
专题09 二次函数的图象与性质（6大考点）
核心考点一 二次函数的图象与性质
例1 （2022·浙江宁波·统考中考真题）点A（m-1，y1），B（m，y2）都在二次函数y=（x-1）2+n的图象上．若y1＜y2，则m的取值范围为（ ）
A．B．C．D．
【答案】B
【分析】根据y1＜y2列出关于m的不等式即可解得答案．
【详解】解：∵点A（m-1，y1），B（m，y2）都在二次函数y=（x-1）2+n的图象上，
∴y1=（m-1-1）2+n=（m-2）2+n，
y2=（m-1）2+n，
∵y1＜y2，
∴（m-2）2+n＜（m-1）2+n，
∴（m-2）2-（m-1）2＜0，
即-2m+3＜0，
∴m＞，
故选：B．
【点睛】本题考查了二次函数图象上点的坐标特征，解题的关键是根据已知列出关于m的不等式．
例2 （2021·江苏常州·统考中考真题）已知二次函数，当时，y随x增大而增大，则实数a的取值范围是（ ）
A．B．C．D．
【答案】B
【分析】根据二次函数的性质，可知二次函数的开口向上，进而即可求解．
【详解】∵二次函数的对称轴为y轴，当时，y随x增大而增大，
∴二次函数的图像开口向上，
∴a-1＞0，即：，
故选B．
【点睛】本题主要考查二次函数的性质，掌握二次函数的开口方向与二次项系数的关系，是解题的关键．
例3 （2022·江苏徐州·统考中考真题）若二次函数的图象上有且只有三个点到x轴的距离等于m，则m的值为________．
【答案】4
【分析】由抛物线解析式可得抛物线对称轴为直线x=1，顶点为（1，-4），由图象上恰好只有三个点到x轴的距离为m可得m=4．
【详解】解：∵，
∴抛物线开口向上，抛物线对称轴为直线x=1，顶点为（1，-4），
∴顶点到x轴的距离为4，
∵函数图象有三个点到x轴的距离为m，
∴m=4，
故答案为：4．
【点睛】本题考查了二次函数图象上点的坐标特征，能够理解题意是解题的关键．
知识点：二次函数的概念及表达式
1.一般地，形如y=ax2+bx+c（a，b，c是常数，a≠0）的函数，叫做二次函数．
2.二次函数解析式的三种形式
（1）一般式：y=ax2+bx+c（a，b，c为常数，a≠0）．
（2）顶点式：y=a（x–h）2+k（a，h，k为常数，a≠0），顶点坐标是（h，k）．
（3）交点式：，其中x1，x2是二次函数与x轴的交点的横坐标，a≠0．
知识点：二次函数的图象及性质
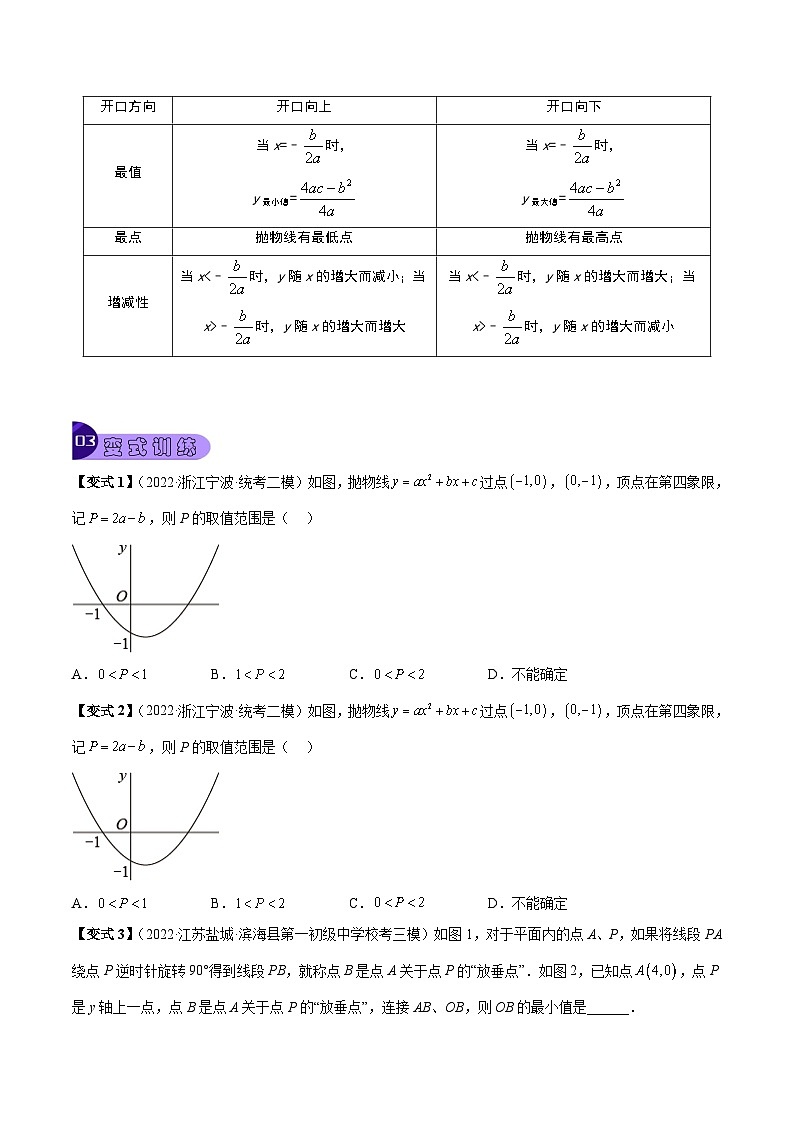
1．二次函数的图象与性质
【变式1】（2022·浙江宁波·统考二模）如图，抛物线过点，，顶点在第四象限，记，则P的取值范围是（ ）
A．B．C．D．不能确定
【答案】B
【分析】根据抛物线经过点(-1,0)、(0,-1)即可得到a-b=1，c=-1，再根据顶点在第四象限，即可求出a的取值范围，则P的取值范围可求．
【详解】∵抛物线过点(-1,0)、(0,-1)，
∴有，且显然a≠0，
∴a-b=1，c=-1，
将抛物线配成顶点式：，
∴顶点坐标为：，
∵抛物线顶点坐标在第四象限，
∴，
∵a-b=1，
∴，
解得：，
∵P=2a-b，a-b=1，
∴P=2a-b=a+a-b=a+1，
∵，
∴，
∴，
故选：B．
【点睛】本题考查了抛物线的图像和性质，根据抛物线经过的点和顶点在第四象限求出的a的取值范围是解答本题的关键．
【变式2】（2022·浙江宁波·统考二模）如图，抛物线过点，，顶点在第四象限，记，则P的取值范围是（ ）
A．B．C．D．不能确定
【答案】B
【分析】根据抛物线经过点(-1,0)、(0,-1)即可得到a-b=1，c=-1，再根据顶点在第四象限，即可求出a的取值范围，则P的取值范围可求．
【详解】∵抛物线过点(-1,0)、(0,-1)，
∴有，且显然a≠0，
∴a-b=1，c=-1，
将抛物线配成顶点式：，
∴顶点坐标为：，
∵抛物线顶点坐标在第四象限，
∴，
∵a-b=1，
∴，
解得：，
∵P=2a-b，a-b=1，
∴P=2a-b=a+a-b=a+1，
∵，
∴，
∴，
故选：B．
【点睛】本题考查了抛物线的图像和性质，根据抛物线经过的点和顶点在第四象限求出的a的取值范围是解答本题的关键．
【变式3】（2022·江苏盐城·滨海县第一初级中学校考三模）如图1，对于平面内的点A、P，如果将线段PA绕点P逆时针旋转90°得到线段PB，就称点B是点A关于点P的“放垂点”．如图2，已知点，点P是y轴上一点，点B是点A关于点P的“放垂点”，连接AB、OB，则OB的最小值是______．
【答案】
【分析】①当P点纵坐标≥0时，过点B作BC⊥y轴于C，由△BPC≌△PAO可得BC=PO，PC=AO，设OP长度为x由两点距离公式建立二次函数，再由二次函数的性质求值即可；②当P点纵坐标＜0时，过点B作BC⊥y轴于C，同理可得OB的表达式，再由二次函数的性质求值即可；
【详解】解：①当P点纵坐标≥0时如图，过点B作BC⊥y轴于C，
∠CBP+∠CPB=90°，∠OPA+∠CPB=90°，则∠CBP=∠OPA，
由旋转的性质可得：PB=PA，
△BPC和△PAO中：∠PBC=∠APO，∠BCP=∠POA=90°，BP=PA，
∴△BPC≌△PAO（AAS），
∴BC=PO，PC=AO，
设OP长度为x，则PC=AO=4，BC=x，B（x，x+4）
∴
∵x≥0，
∴x=0时OB最小，最小值为4，
②当P点纵坐标＜0时，如图，过点B作BC⊥y轴于C，
同理可得△BPC≌△PAO（AAS），BC=PO，PC=AO，
设OP长度为x，则PC=AO=4，BC=x，B（-x，4-x）
∴
∵x＞0，
∴x=2时OB最小，最小值为，
综上所述：OB最小值为，
故答案为：；
【点睛】本题考查了旋转的性质，全等三角形的判定和性质，勾股定理，二次函数的性质；根据P点位置分类讨论是解题关键．
【变式4】（2022·吉林长春·校考模拟预测）定义：我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”．如图，在正方形OABC中，点，点，则互异二次函数与正方形OABC有公共点时m的最大值是__________．
【答案】
【分析】根据抛物线顶点横纵坐标的关系得出抛物线顶点的运动轨迹，结合正方形的位置，则可得到当抛物线经过点B时m取最大值，依此列式求解即可．
【详解】解：∵抛物线顶点坐标为 ,
∴抛物线顶点在直线y= -x上移动，
∵四边形AOBC为正方形，点A（0，2），点C（2，0），
∴点B坐标为，
如图，当抛物线经过点B时，m取最大值，
将代入中，
则，
解得 或（舍去），
故答案为：．
【点睛】本题考查二次函数图象和性质和图象平移的特点，解题关键是掌握二次函数图象与系数的关系及图象平移的特点．
【变式5】（2021·湖北随州·一模）如图，抛物线与轴交于A，B两点点B在点A的右侧，其顶点为C，点P为线段上一点，且过点P作，分别交抛物线于，两点点在点的右侧，连接，．
(1)直接写出A，B，C三点的坐标；用含，的式子表示
(2)猜想线段与之间的数量关系，并证明你的猜想；
(3)若，，求的值．
【答案】(1)点A，B，C的坐标分别为、、
(2)，理由见解析
(3)
【分析】（1），求出x的值，可得点A，B的坐标，令，求出y的值，可得点C的坐标；
（2）根据求出点P的纵坐标，代入解析式，求出点D，E的横坐标,进而求出DE的长度，再根据点A，B的坐标求出AB的长度，即可得出；
（3）当时，求出OP，PC，PD，再通过导角证明，得出，进而得出，代入即可求解．
（1）
解：对于，
令，解得，
令，则，
故点A，B，C的坐标分别为、、；
（2）
解：，理由：
∵，点C在y轴负半轴，
∴，
∴，
则，
故点的坐标为，
当时，则，
解得，
则，
由点A，B的坐标得：，
∴；
（3）
解：当时，
由知，点的坐标为，点C的坐标为，，
∴，，，，
∵，
∴，
又∵，
，
，
∴，即，
∴，
解得．
【点睛】本题主要考查二次函数的图象和性质，有一定的综合性，难度适中，第三问利用三角函数或三角形相似均可得出，解题的关键是熟练掌握二次函数的图象及性质．
核心考点二 与二次函数图象有关的判断
例1 （2021·广西河池·统考中考真题）点均在抛物线上，下列说法正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
【答案】D
【详解】解：由图象，根据二次函数的性质，有
A．若，则，原说法错误；
B．若，则，原说法错误；
C．若，则，原说法错误；
D．若，则，原说法正确．
故选D．
【点睛】本题考查二次函数的图象和性质．
例2 （2021·湖南娄底·统考中考真题）用数形结合等思想方法确定二次函数的图象与反比例函数的图象的交点的横坐标所在的范围是（ ）
A．B．C．D．
【答案】D
【分析】在同一个直角坐标系中画出两个函数的图象，来判断出交点横坐标所在的范围．
【详解】解：在同一个直角坐标系中画出两个函数的图象，如下图：
由图知，显然，
当时，将其分别代入与计算得；
，
，
此时反比例函数图象在二次函数图象的上方，
故选：D．
【点睛】本题考查了二次函数和反比例函数的图象，解题的关键是：准确画出函数的图象，再通过关键点得出答案．
例3 （2020·广西贵港·中考真题）如图，对于抛物线，，，给出下列结论：①这三条抛物线都经过点；②抛物线的对称轴可由抛物线的对称轴向右平移1个单位而得到；③这三条抛物线的顶点在同一条直线上；④这三条抛物线与直线的交点中，相邻两点之间的距离相等．其中正确结论的序号是_______________．
【答案】①②④
【分析】根据抛物线图象性质及配方法解题．
【详解】将分别代入抛物线，，中，可知，这三条抛物线都经过点C，故①正确；
抛物线的对称轴为，
抛物线的对称轴为，可由向右平移1个单位而得到，故②正确；
抛物线的顶点为A
抛物线的顶点为B
抛物线的顶点为C
，
三条抛物线的顶点不在同一条直线上，故③错误；
将分别代入三条抛物线，得0或1，0或2，0或3，
可知，相邻两点之间的距离相等，故④正确，
综上所述，正确的是①②④，
故选：①②④．
【点睛】本题考查二次函数的性质，其中涉及将一般式化为顶点式等知识，是重要考点，难度较易，掌握相关知识是解题关键．
知识点、抛物线的三要素：开口方向、对称轴、顶点.
①决定抛物线的开口方向：
当时，开口向上；当时，开口向下；相等，抛物线的开口大小、形状相同.
②平行于轴(或重合)的直线记作.特别地，轴记作直线.
顶点决定抛物线的位置.几个不同的二次函数，如果二次项系数相同，那么抛物线的开口方向、开口大小完全相同，只是顶点的位置不同.
知识点、求抛物线的顶点、对称轴的方法
(1)公式法：，∴顶点是，
对称轴是直线.
(2)配方法：运用配方法将抛物线的解析式化为的形式，
得到顶点为(,)，对称轴是.
(3)运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，所以对称轴的连线的垂直平分线是抛物线的对称轴，对称轴与抛物线的交点是顶点.
★用配方法求得的顶点，再用公式法或对称性进行验证，才能做到万无一失★
知识点、直线与抛物线的交点
(1)轴与抛物线得交点为()

(2)与轴平行的直线与抛物线有且只有一个交点(,).

(3)抛物线与轴的交点
二次函数的图像与轴的两个交点的横坐标、，是对应一元二次方程
的两个实数根.抛物线与轴的交点情况可以由对应的一元二次方程的根的判别式判定：
①有两个交点抛物线与轴相交；
②有一个交点(顶点在轴上)抛物线与轴相切；
③没有交点抛物线与轴相离.
(4)平行于轴的直线与抛物线的交点
同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时，两交点的纵坐标相等，设纵坐标为，则横坐标是的两个实数根.
(5)一次函数的图像与二次函数的图像的交点，由方程组
的解的数目来确定：
①方程组有两组不同的解时与有两个交点;
②方程组只有一组解时与只有一个交点；③方程组无解时与没有交点.
(6)抛物线与轴两交点之间的距离：若抛物线与轴两交点为，由于、是方程的两个根，故
【变式1】（2022·四川泸州·校考模拟预测）二次函数（）的自变量与函数的部分对应值如下表：
则这个函数图像的顶点坐标是（ ）
A．B．C．D．
【答案】A
【分析】由图表数据可知，函数图像与轴的两个交点为和，故可知图像对称轴为：，即可对照表格得出顶点坐标．
【详解】解：由表可知：当时，；当时，，即函数图像与轴的两个交点为和，
由此可知：图像对称轴为：，对照表格可知：当时，，
即顶点为，
故选：A．
【点睛】本题考查了二次函数的性质，关键是将表格数据转化为点的坐标信息，结合二次函数性质画出草图分析．
【变式2】（2022·山东日照·校考一模）设，，是抛物线上的三点，则，，的大小关系为（ ）
A．B．
C．D．
【答案】A
【分析】把点的坐标分别代入抛物线解析式可求得y1，y2，y3的值，比较大小即可．
【详解】解：∵，，是抛物线上的三点，
∴，，，
∵1＞-2＞-7，
∴，
故选：A．
【点睛】本题主要考查二次函数图象上点的坐标特征，掌握函数图象上点的坐标满足函数解析式是解题的关键．
【变式3】（2021·陕西西安·校考模拟预测）在同一坐标系中，二次函数，，的图象如图，则，，的大小关系为______（用“”连接）
【答案】
【分析】抛物线的开口方向和开口大小由的值决定的，系数绝对值越大，开口越小．
【详解】解：∵抛物线开口都向上，
∴二次项系数都大于0.
二次函数的开口最小，二次函数的开口最大，
，
故答案为：．
【点睛】本题考查了二次函数y=ax2（a≠0）的性质，是基础知识，需熟练掌握．熟练掌握抛物线开口大小与|a|有关，|a|越大图象开口越小，|a|越小图象开口越大是解答本题的关键．
【变式4】（2022·广西·统考二模）如图，抛物线与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则a的取值范围是______．
【答案】
【分析】顶点C是矩形DEFG上（包括边界和内部）的一个动点，当顶点C与D点重合，可以知道顶点坐标为（1，3）且抛物线过（﹣1，0），则它与x轴的另一个交点为（3，0），由此可求出a；当顶点C与F点重合，顶点坐标为（3，2）且抛物线过（-2，0），则它与x轴的另一个交点为（8，0），由此也可求a，然后由此可判断a的取值范围．
【详解】顶点C是矩形DEFG上（包括边界和内部）的一个动点，
当顶点C与D点重合，顶点坐标为（1，3），则抛物线解析式y=a（x﹣1）2+3，
由，解得﹣≤a≤﹣；
当顶点C与F点重合，顶点坐标为（3，2），则抛物线解析式y=a（x﹣3）2+2，
由，解得﹣≤a≤﹣；
∵顶点可以在矩形内部，
∴．
故答案为：
【点睛】本题考查了二次函数图象的性质，矩形的性质，二次函数的平移，掌握二次函数的性质是解题的关键．
【变式5】（2022·河南南阳·统考三模）在平面直角坐标系中，已知抛物线．
(1)抛物线的对称轴为直线_______，抛物线与y轴的交点坐标为_______；
(2)若当x满足时，y的最小值为，求此时y的最大值．
【答案】(1)，
(2)当时，y的最大值为12，当时，y的最大值为
【分析】（1）根据对称轴的表达式计算求值，再令x=0求得y值即可解答；
（2）分两种情况讨论：①当时，抛物线开口向上，可得时y取得最小值，进而可得抛物线解析式，由对称轴x=2可得，x=5时y取得最大值；②当时，抛物线开口向下，可得可得x=5时y取得最小值，x=2时y取得最大值，计算求值即可；
(1)
解：抛物线的对称轴为x=，
令x=0，则y=2，
∴抛物线与y轴的交点坐标为（0，2）；
(2)
解：①当时，抛物线开口向上，
∴时，y取得最小值，
，解得，
∴该抛物线的解析式为，
∵，抛物线的对称轴为x=2，
∴当时，y取得最大值，
；
②当时，抛物线开口向下，
∵，抛物线的对称轴为x=2，
∴当时，y取得最小值，
，解得，
∴该抛物线的解析式为，
当时，y取得最大值，
，
综上所述，当时，y的最大值为12，当时，y的最大值为；
【点睛】本题考查了二次函数的解析式，二次函数的对称性，求二次函数的最值，根据a的正负分类讨论是解题关键．
核心考点三 与系数a、b、c有关的判断
例1 （2022·湖北黄石·统考中考真题）已知二次函数的部分图象如图所示，对称轴为直线，有以下结论：①；②若t为任意实数，则有；③当图象经过点时，方程的两根为，（），则，其中，正确结论的个数是（ ）
A．0B．1C．2D．3
【答案】D
【分析】利用抛物线开口方向得到a＞0，利用抛物线的对称轴方程得到，利用抛物线与y轴的交点位置得到c＜0，则可对①进行判断；利用二次函数当x=-1时有最小值可对②进行判断；由于二次函数与直线y=3的一个交点为（1，3），利用对称性得到二次函数y=ax2+bx+c与直线y=3的另一个交点为（-3，3），从而得到x1=-3，x2=1，则可对③进行判断．
【详解】∵抛物线开口向上，
∴，
∵抛物线的对称轴为直线，即，
∴，
∵抛物线与y轴的交点在x轴下方，
∴，
∴，所以①正确；
∵时，y有最小值，
∴（t为任意实数），即，所以②正确；
∵图象经过点时，代入解析式可得，
方程可化为，消a可得方程的两根为，，
∵抛物线的对称轴为直线，
∴二次函数与直线的另一个交点为，
，代入可得，
所以③正确．
综上所述，正确的个数是3．
故选D．
【点睛】本题考查了二次函数图象与系数的关系：二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时，对称轴在y轴左；当a与b异号时，对称轴在y轴右．常数项c决定抛物线与y轴交点：抛物线与y轴交于（0，c）．
例2 （2022·山东日照·统考中考真题）已知二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，对称轴为，且经过点（-1，0）．下列结论：①3a+b=0；②若点，（3，y2）是抛物线上的两点，则y1