最新中考数学总复习真题探究与变式训练（讲义） 专题36 圆的相关计算与证明（5大类型）

这是一份最新中考数学总复习真题探究与变式训练（讲义） 专题36 圆的相关计算与证明（5大类型），文件包含专题36圆的相关计算与证明5大类型原卷版docx、专题36圆的相关计算与证明5大类型解析版docx等2份试卷配套教学资源，其中试卷共128页， 欢迎下载使用。
一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。
模块三 重难点题型专项训练
专题36 圆的相关计算与证明（5大类型 ）
考查题型一 圆与锐角三角函数的综合
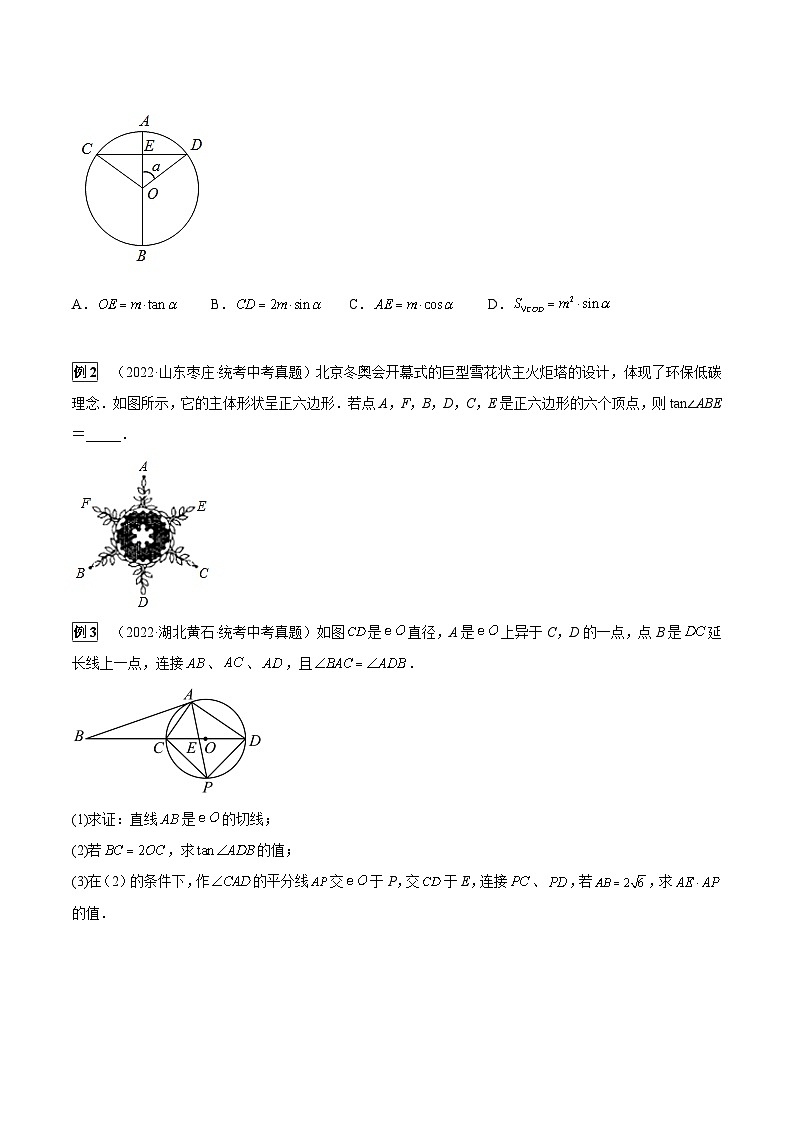
例1 （2021·浙江丽水·统考中考真题）如图，是的直径，弦于点E，连结．若的半径为，则下列结论一定成立的是（ ）
A．B．C．D．
例2 （2022·山东枣庄·统考中考真题）北京冬奥会开幕式的巨型雪花状主火炬塔的设计，体现了环保低碳理念．如图所示，它的主体形状呈正六边形．若点A，F，B，D，C，E是正六边形的六个顶点，则tan∠ABE＝_____．
例3 （2022·湖北黄石·统考中考真题）如图是直径，A是上异于C，D的一点，点B是延长线上一点，连接、、，且．
(1)求证：直线是的切线；
(2)若，求的值；
(3)在（2）的条件下，作的平分线交于P，交于E，连接、，若，求的值．
解题策略一：利用圆的有关性质构造直角三角形
如果圆中存在直径，则可根据直径所对的圆周角是直角构造直角三角形，从而为使用三角函数创造条件.垂径定理和切线的性质也是圆中构造直角的重要依据.
解题策略二：用圆周角的性质把角转化到直角三角形中
借助同孤或等弧所对的圆周角相等或其他相等关系，可把三角函数中涉及的锐角转化为直角三角形中的锐角，然后借助三角函数的定义解答.
总而言之，圆与三角函数都是初中数学知识的重点，也是难点，将这两部分知识综合考查时，难度相对较大。其解题关键在于，找到相关的直角三角形。若没有现成的直角三角形，则需根据所给的条件，合理构造直角三角形，或把角转化到直角三角形中解答。
圆的内容在考察的时候形式多样，不管是哪一种类型都可以随机结合，对于学生而言灵活变通能力要求较高，所以在平时做题时需要多做总结和同类型整理，才能更快融会贯通。
【变式1】（2022·江西·模拟预测）如图，、分别与相切于点、，连接并延长与交于点、，若，，则的值为（ ）
A．B．C．D．
【变式2】（2022·贵州遵义·统考二模）如图，AB为的直径，延长AB到点P，过点P作的切线PC，PD，切点分别为C，D，连接CD交AP于点M，连接BD，AD．若，，则AD的长为（ ）
A．B．C．2D．
【变式3】（2022·广东云浮·校联考三模）如图，是的弦，半径于点D，且，，则_____．
【变式4】（2022·四川广元·统考一模）如图，AB为的直径，点P在AB的延长线上，PC，PD分别与相切于点C，D，连接AC，AD．若，，则______．
【变式5】（2022·山东济宁·校考二模）如图，点是中弦的中点，过点作的直径，是上一点，过点作的切线，与的延长线交于，与的延长线交于点，连接与交于点．
(1)求证：；
(2)若点是的中点，，半径长为6，求长．
考查题型二 圆基本性质的证明与计算
例1 （2022·山东泰安·统考中考真题）如图，四边形中．，，交于点E，以点E为圆心，为半径，且的圆交于点F，则阴影部分的面积为（ ）
A．B．C．D．
例2 （2022·浙江嘉兴·统考中考真题）如图，在扇形中，点C，D在上，将沿弦折叠后恰好与，相切于点E，F．已知，，则的度数为_______；折痕的长为_______．
例3 （2022·辽宁大连·统考中考真题）是的直径，C是上一点，，垂足为D，过点A作的切线，与的延长线相交于点E．
(1)如图1，求证；
(2)如图2，连接，若的半径为2，，求的长．
知识点、圆的对称性
（1）对称中心
圆既是中心对称图形，又是轴对称图形和旋转对称图形。
将圆周绕圆心旋转180°能与自身重合，因此它是中心对称图形，它的对称中心是圆心。将圆周绕圆心旋转任意一个角度都能与自身重合，这说明圆是旋转对称图形。
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。
在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么他们所对应的其余各组量都分别相等。
将整个圆分为等份，每一份的弧对应的圆心角，我们也称这样的弧为的弧。圆心角的度数和它所对的弧的度数相等．
（2）对称轴
经过圆心画任意一条直线，并沿此直线将圆对折，直线两旁的部分能够完全重合，所以圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴，所以圆有无数条对称轴。
（3）垂径定理
1．垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；
几何语言：

垂径定理的几个基本图形：
垂径定理在基本图形中的应用：
2．其它正确结论：
⑴ 弦的垂直平分线经过圆心，并且平分弦所对的两条弧；
⑵ 平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．
⑶ 圆的两条平行弦所夹的弧相等．
3．知二推三：①直径或半径；②垂直弦；③平分弦；④平分劣弧；⑤平分优弧．以上五个条件知二推三．
注意：在由①③推②④⑤时，要注意平分的弦非直径．
4．常见辅助线做法：
⑴过圆心，作垂线，连半径，造，用勾股，求长度；
⑵有弧中点，连中点和圆心，得垂直平分．
【变式1】（2022·广东广州·广州市第一中学校考三模）如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，AC，BC的中点分别是M，N，PQ若MP+NQ=12，AC+BC=18，则AB的长为（ ）
A．B．C．D．
【变式2】（2022·福建福州·福建省福州教育学院附属中学校考模拟预测）如图，的三个顶点、、均在上，且对角线过圆心，与相切于点，若的半径为，则▱的面积为（ ）
A．B．C．D．
【变式3】（2022·辽宁鞍山·模拟预测）如图，为的直径，点是弧的中点，过点作于点，延长交于点，若，，则的直径长为______．
【变式4】（2022·湖南株洲·统考模拟预测）如图，在半径为3的⊙O中，AB是直径，AC是弦，D是的中点，AC与BD交于点E．若E是BD的中点，则AC的长是_______．
【变式5】（2022·贵州铜仁·模拟预测）已知：如图，的直径与弦相交于点，，的切线与弦的延长线相交于点
(1)求证：；
(2)连接，若的半径为，，求线段，的长.
考查题型三 与圆的切线有关的证明与计算
例1 （2022·重庆·统考中考真题）如图，是的直径，C为上一点，过点C的切线与的延长线交于点P，若，则的长为（ ）
A．B．C．D．3
例2 （2022·内蒙古呼和浩特·统考中考真题）已知为⊙的直径且，点是⊙上一点（不与、重合），点在半径上，且，与过点的⊙的切线垂直，垂足为．若，则_____，_______．
例3 （2022·内蒙古·中考真题）如图，是的外接圆，与相切于点D，分别交，的延长线于点E和F，连接交于点N，的平分线交于点M．
(1)求证：平分；
(2)若，，求线段的长．
切线的定义是：一直线若与一圆有且只有一个交点，那么这条直线就是圆的切线。一般如果题目给出有切线，那么我们可以考虑添加过切点的半径，进而连接圆心和切点，利用切线的性质和定理构造出直角或直角三角形，从而使用勾股定理解出一些边角关系。
【变式1】（2022·四川绵阳·东辰国际学校校考模拟预测）如图，直线与x轴、y轴分别交于A、B两点，，与y轴相切于点O，将向上平移m个单位长度，当与直线AB第一次相切时，则m的值是（ ）
A．B．C．D．
【变式2】（2022·浙江宁波·一模）如图，Rt△ABC中，∠ACB=90°，CD⊥AB，AC=10，BC=24，点P是线段CD上一动点，当半径为6的⊙P与△ABC的一边相切时，CP的长为___________．
【变式3】（2022·广东韶关·校考三模）如图，是的直径，是的平分线交于点，过作的切线交的延长线于点．若，，则的长为______．
【变式4】（2022·广东广州·校考二模）如图，已知，，．
(1)在边上求作点，连接，使（要求：尺规作图，不写作法，保留作图痕迹）；
(2)在第（1）问图中，若，
求；
已知经过点的圆与相切于点，求扇形的面积．
考查题型四 圆与相似三角形的综合
例1 （2021·辽宁锦州·统考中考真题）如图，△ABC内接于⊙O，AB为⊙O的直径，D为⊙O上一点（位于AB下方），CD交AB于点E，若∠BDC＝45°，BC＝6，CE＝2DE，则CE的长为（ ）
A．2B．4C．3D．4
例2 （2022·湖南岳阳·统考中考真题）如图，在中，为直径，，为弦，过点的切线与的延长线交于点，为线段上一点（不与点重合），且．
（1）若，则的长为______（结果保留）；
（2）若，则______．
例3 （2022·山东淄博·统考中考真题）已知△ABC是⊙O的内接三角形，∠BAC的平分线与⊙O相交于点D，连接DB．
(1)如图1，设∠ABC的平分线与AD相交于点I，求证：BD=DI；
图1
(2)如图2，过点D作直线DEBC，求证：DE是⊙O的切线；
图2
(3)如图3，设弦BD，AC延长后交⊙O外一点F，过F作AD的平行线交BC的延长线于点G，过G作⊙O的切线GH（切点为H），求证：GF=GH．
图3
我们知道在圆中随便相连就可以形成很多三角形，而圆是轴对称图形，有无数条对称轴，这就造成了圆的一些特殊性质，比如：
（1）直径所对的圆周角为直角；
（2）平分一般弦（不是直径）的直径垂直于弦；
（3）圆的切线与过该点的半径垂直等。
因此，圆中有非常多的直角三角形，且圆中三角形的相似一般是直角三角形的相似。
这些相似包括：A字相似（平行、不平行）；8字相似（平行、不平行）、摄影相似、母子相似等。
【变式1】（2021·贵州遵义·校考模拟预测）如图，在平行四边形中，以对角线为直径的分别交于M，N．若，则的长度为（ ）
A．12B．15C．D．
【变式2】（2022·重庆沙坪坝·重庆南开中学校考三模）如图，点E是⊙O中弦AB的中点，过点E作⊙O的直径CD，P是⊙O上一点，过点P作⊙O的切线与AB延长线交于点F，与CD延长线交于点G，若点P为FG中点，，⊙O的半径长为3则CE的长为（ ）
A．B．C．D．
【变式3】（2023·广西玉林·一模）如图，点在以为直径的半圆上运动点不与点，重合，于点，平分，交于点，交于点若，则______．
【变式4】（2022·陕西西安·校考三模）如图半径为，为直径，弦，点是半圆弧上的动点（不与A、重合），过点作的垂线交的延长线于点，则面积的最大值为______．
【变式5】（2022·广东云浮·校联考三模）如图1，⊙O是的外接圆，是直径，，交⊙O于点E，且．

(1)求证：是⊙O的切线；
(2)若点E为线段的中点，判断以O、A、C、E为顶点的四边形的形状并证明；
(3)如图2，作于点F，连接交于点G，求的值．
考查题型五 扇形面积与圆锥侧面积的综合
例1 （2022·宁夏·中考真题）把量角器和含角的三角板按如图方式摆放：零刻度线与长直角边重合，移动量角器使外圆弧与斜边相切时，发现中心恰好在刻度处，短直角边过量角器外沿刻度处（即，）．则阴影部分的面积为（ ）
A．B．
C．D．
例2 （2022·辽宁朝阳·统考中考真题）如图，在矩形ABCD中，AD＝2，DC＝4，将线段DC绕点D按逆时针方向旋转，当点C的对应点E恰好落在边AB上时，图中阴影部分的面积是_____．
例3 （2022·山东日照·统考中考真题）如图，在Rt△ABC中，∠C=90°，∠B=30°，点D为边AB的中点，点O在边BC上，以点O为圆心的圆过顶点C，与边AB交于点D．
(1)求证：直线AB是⊙O的切线；
(2)若，求图中阴影部分的面积．
知识点、弧长及扇形的面积
设的半径为，圆心角所对弧长为，
（一）弧长的计算
（1）弧长公式：
（2）公式推导：在半径为的圆中，因为的圆心角所对的弧长就是圆周长，所以的圆心角所
对的弧长是即于是的圆心角所对的弧长为
注意：（1）在弧长公式中，表示的圆心角的倍数，不带单位。例如圆的半径，计算的圆心角
所对弧长时，不要错写成
（2）在弧长公式中，已知，中的任意两个量，都可以求出第三个量。
（二）扇形面积的计算
（1）扇形的定义：由组成圆心角的两条半径和圆心角所对的弧围成的图形叫作扇形。
（2）扇形的面积：为扇形所在圆的半径，为扇形的弧长。
（3）公式推导：
①在半径为的圆中，因为360°的圆心角所对的扇形的面积就是圆面积，所以圆心角是的扇形面积是于是圆心角为的扇形面积是
②即其中为扇形的弧长，为半径。
点拨：（1）扇形面积公式与三角形的面积公式有些类似，只需把扇形看成一个曲边三角形，把弧长看成底，半径看成高即可。
（2）在求扇形面积时，可根据已知条件来确定是使用公式还是
（3）已知四个量中任意两个，都可以求出另外两个。
（4）公式中的“”与弧长公式中的“”的意义是一样的，表示“”的圆心角的倍数，计算时不带单位。

知识点、圆锥的侧面积与全面积
（1）圆锥的有关概念：圆锥是由一个底面和一个侧面围面的几何体（如图所示）。连接圆锥顶点和底面圆周上任意一点的线段叫作圆锥的母线，连接顶点与底面圆心的线段叫作圆锥的母线，连接顶点与底面圆心的线段叫作圆锥的高。
圆锥可以看作是一个直角三角形绕它的一条直角边所在的直线旋转一周所形成的图形，故圆锥的母线、高、底面半径恰好构成一个直角三角形，满足。已知任意两个量，可以求出第三个量。

（2）圆锥的侧面展开图（如图1-49-4所示）：沿着圆锥的母线可把圆锥的侧面展开，圆锥的侧面展开图是扇形，这个扇形的半径等于圆锥的母线长，弧长等于圆锥底面圆的周长。
（3）圆锥的侧面积就是弧长为圆锥底面圆的周长、半径为圆锥的母线长的扇形面积，
计算公式为：
圆锥的全面积就是它的侧面积与它的底面积之和，其计算公式为。
【变式1】（2022·宁夏固原·校考一模）如图，在中，，点O在上，经过点A的与相切于点D，交于点E，若则图中阴影部分面积为（ ）
A．B．C．D．
【变式2】（2022·四川乐山·统考二模）如图，在中，，，斜边的两个端点分别在相互垂直的射线和上滑动，给定下列命题，其中正确命题的序号是（ ）．
①若、两点关于对称，则；
②、两点距离的最大值为；
③若平分，则；
④斜边的中点运动路径的长为．
A．①③④B．②③④C．①④D．①②
【变式3】（2022·四川遂宁·校联考一模）如图，在矩形中，，，以为圆心，长为半径画弧交于点，以为圆心，长为半径画弧交的延长线于点，则图中阴影部分的面积是_____．
【变式4】（2022·山东泰安·校考二模）如图，在扇形中，，平分交于点D，点E为半径的中点．若，则阴影部分的面积为________．
【变式5】（2022·河北沧州·统考二模）石家庄市水上公园南侧新建的摩天轮吸引了附近市民的目光．据工作人员介绍，新建摩天轮直径为100m，最低点距离地面1m，摩天轮的圆周上均匀地安装了24个座舱（本题中将座舱视为圆周上的点），游客在距离地面最近的位置进舱，运行一圈时间恰好是13分14秒，寓意“一生一世”．小明从摩天轮的底部出发开始观光，摩天轮转动1周．
(1)小明所在座舱到达最高点时距离地面的高度为 m；
(2)在小明进座舱后间隔3个座舱小亮进入座舱（如图，此时小明和小亮分别位于P、Q两点），
①求两人所在座舱在摩天轮上的距离（弧的长）；
②求此时两人所在座舱距离地面的高度差；
(3)受周围建筑物的影响，当乘客与地面的距离不低于时，可视为最佳观赏位置，求最佳观赏时间有多长（不足一分钟按一分钟记）．
【培优练习】
1．（2021·浙江·九年级自主招生）如图所示，，求的值为（ ）
A．4B．6C．7D．12
2．（2022·浙江·九年级自主招生）如图，是的外接圆，是的直径，D是的中点，连接交于点E，连接，且，若，则的长为（ ）
A．6B．C．D．
3．（2023秋·河北邯郸·九年级统考期末）如图，将量角器和含角的一块直角三角板紧靠着放在同一平面内，使、、在一条直线上，且，过点作量角器圆弧所在圆的切线，切点为，则点在量角器上所对应的锐角度数是（ ）
A．B．C．D．
4．（2023秋·河北承德·九年级统考期末）如图，甲、乙、丙、丁四位同学从四块全等的等腰直角三角形纸板上裁下四块不同的纸板（阴影部分），使得阴影面积尽可能大，他们的具体裁法如下：
甲同学：如图1所示裁下一个正方形，面积记为；
乙同学：如图2所示裁下一个正方形，面积记为；
丙同学：如图3所示裁下一个半圆，使半圆的直径在等腰的直角边上，面积记为；
丁同学：如图所示裁下一个内切圆，面积记为；
则下列判断正确的是（ ）
①；②；③在，，，中，最小
A．①②B．②③C．①③D．①②③
5．（2022秋·河北沧州·九年级统考期末）如图，在中，，，，半径为1的在内平移（可以与该三角形的边相切），则点到上的点的距离的最大值为（ ）
A．B．C．D．
6．（2022秋·河北石家庄·九年级校联考期末）如图，已知为等腰直角三角形，，以点为圆心，为半径作圆，点为上一动点，连接，并绕点顺时针旋转得到，连接，则的最小值是( )
A．B．C．D．
7．（2023秋·安徽合肥·九年级校考期末）如图，中，，，，是平面内一动点，且，取的中点，连接，则线段的最大值为（ ）
A．B．C．D．
8．（2023秋·河北秦皇岛·九年级校联考期末）如图，在半径为2的中，为直径，弦且过半径的中点，为上一动点，于点，当从点出发顺时针运动到点时，点所经过的路径长为（ ）
A．B．C．D．
9．（2022秋·四川广元·九年级校考阶段练习）如图，矩形纸片中，，把它分割成正方形纸片和矩形纸片后，分别裁出扇形和半径最大的圆，恰好能作为同一个圆锥的侧面和底面，则该圆锥的高为______．
10．（2021·浙江·九年级自主招生）如图，在中，，以该三角形的三条边为边向形外作正方形，正方形的顶点E，F，G，M，N都在同一个圆上．记该圆面积为，面积为，则的值是_________．
11．（2022·浙江·九年级自主招生）如图，在半径为1的中，引两条互相垂直的直径和，在上取点C，弦交于P，弦交于Q，则四边形的面积为_________．
12．（2021秋·河南信阳·九年级校考期末）如图，在矩形中，，．将矩形绕点逆时针旋转至矩形的位置，此时边恰好经过点，其中点的运动路径是弧，则图中阴影部分的面积为___________．
13．（2022秋·江苏连云港·九年级校考阶段练习）如图，为的直径，点为上一点，将劣弧沿弦翻折交于点，连接．若点与圆心不重合，，则的度数是______．
14．（2022秋·湖北恩施·九年级校考阶段练习）如图，点在以为直径的半圆上，，，点在上运动，点与点关于对称，于点，并交的延长线于点．下列结论：①；②线段的最小值为；③当时，与半圆相切；④当点从点运动到点时，线段扫过的面积是．其中正确的序号是________．
15．（2022秋·辽宁盘锦·九年级校考期中）如图，是的直径，和是它的两条切线，切于点E，交于点D，交于点C．
(1)求证：；
(2)如果，，F为的中点，连接，求．
16．（2022秋·陕西渭南·九年级统考期末）如图，在中，，点在上，以点为圆心，长为半径的圆与、分别交于点、，且．
(1)求证：是的切线；
(2)若，，求的长．
17．（2023秋·广东江门·九年级校考期末）如图，为的外接圆，，D为与的交点，E为线段延长线上一点，且．
(1)求证：直线是的切线．
(2)若，，求的半径；
(3)在（2）的基础上，点F在上，且，的内心点G在边上，求的长．
18．（2023秋·福建莆田·九年级统考期末）如图，在中，，点D是边的中点，点O在边上，经过点C且与边相切于点E，．
(1)求证：是的切线；
(2)若，，求的半径．
19．（2022秋·辽宁盘锦·九年级校考期中）如图，四边形内接于，是直径，，连接，，过点D的直线与的延长线相交于点E，且．
(1)求的度数．
(2)若，，求，的长．
(3)若，，直接写出的长．
20．（2022秋·广东汕头·九年级统考期末）如图，是的直径，点C是上一点，与过点C的切线垂直，垂足为点D，直线与的延长线相交于点P，G是的内心，连接并延长，交于E，交于点F，连接．
(1)求证：平分；
(2)连接，判断的形状，并说明理由；
(3)若，，求线段的长．
考查类型
考查类型一 圆与锐角三角函数的综合
考查类型二 圆基本性质的证明与计算
考查类型三 与圆的切线有关的证明与计算
考查类型四 圆与相似三角形的综合
考查类型五 扇形面积与圆锥侧面积综合
新题速递