最新中考数学总复习真题探究与变式训练（讲义） 专题37 二次函数的性质综合题（4大类型）

这是一份最新中考数学总复习真题探究与变式训练（讲义） 专题37 二次函数的性质综合题（4大类型），文件包含专题37二次函数的性质综合题4大类型原卷版docx、专题37二次函数的性质综合题4大类型解析版docx等2份试卷配套教学资源，其中试卷共125页， 欢迎下载使用。
一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。
模块三 重难点题型专项训练
专题37 二次函数的性质综合题（4大类型）
考查类型一 交点问题
例1 （2022·山东烟台·统考中考真题）二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，其对称轴为直线x＝﹣，且与x轴的一个交点坐标为（﹣2，0）．下列结论：①abc＞0；②a＝b；③2a+c＝0；④关于x的一元二次方程ax2+bx+c﹣1＝0有两个相等的实数根．其中正确结论的序号是（ ）
A．①③B．②④C．③④D．②③
例2 （2022·湖北荆州·统考中考真题）规定：两个函数，的图象关于y轴对称，则称这两个函数互为“Y函数”．例如：函数与的图象关于y轴对称，则这两个函数互为“Y函数”．若函数（k为常数）的“Y函数”图象与x轴只有一个交点，则其“Y函数”的解析式为______．
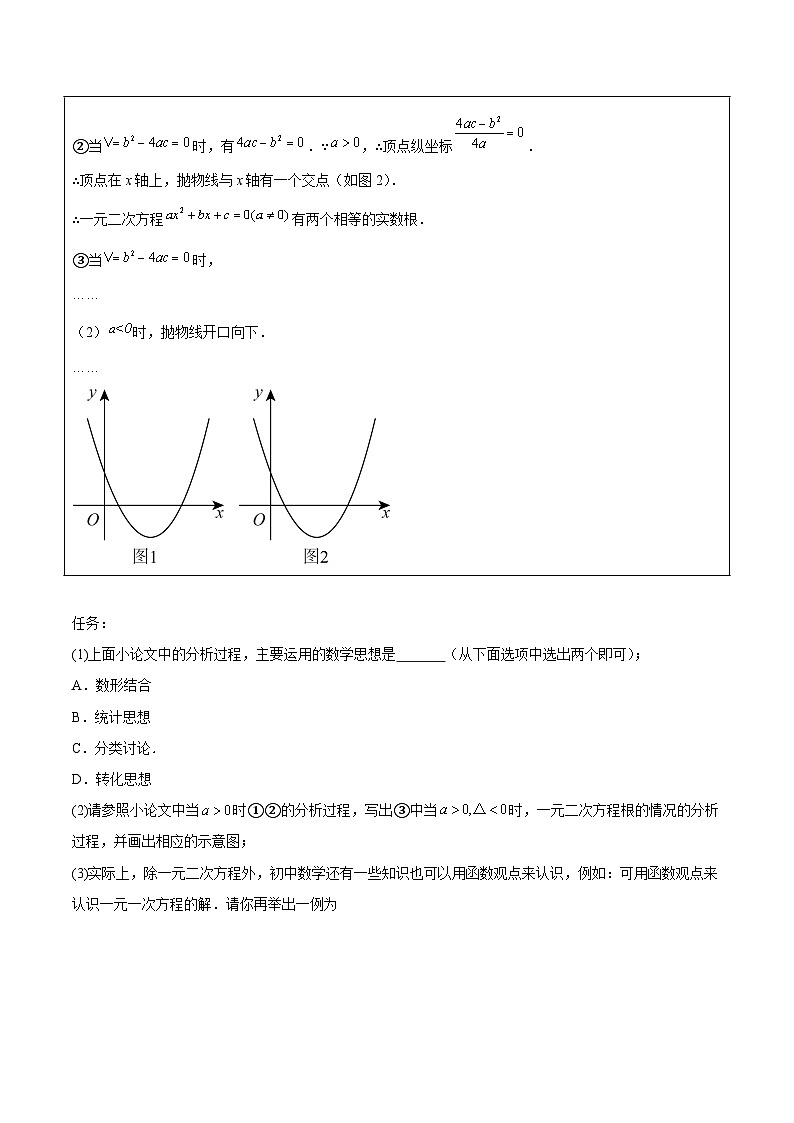
例3 （2022·山西·中考真题）阅读与思考
下面是小宇同学的数学小论文，请仔细阅读并完成相应的任务
任务：
(1)上面小论文中的分析过程，主要运用的数学思想是 （从下面选项中选出两个即可）；
A．数形结合
B．统计思想
C．分类讨论．
D．转化思想
(2)请参照小论文中当时①②的分析过程，写出③中当时，一元二次方程根的情况的分析过程，并画出相应的示意图；
(3)实际上，除一元二次方程外，初中数学还有一些知识也可以用函数观点来认识，例如：可用函数观点来认识一元一次方程的解．请你再举出一例为
二次函数与X轴的交点有三种可能，分别是有两个交点、一个交点和无交点。在初中范围内，二次函数与Y轴始终有交点（当x=0时，y必有一个值）。在实际解题中，与Y轴的交点纵坐标的值，就是函数表达式中c的值。
二次函数与X轴若有两个交点，则求根公式大于0，如果一个交点，则求根公式等于0，如果无交点，则求根公式小于0。通常情况下，二次函数的求解中都是有两个交点。只是要注意，不同的题型，不同的情况下求解方法也不同。总之在求解中要灵活应用各种公式，巧妙应对，解题就变得轻巧。
二次函数与X轴交点的求解方法
以上简要介绍二次函数与X轴的交点，而在实际情况中，更加的复杂，下面从常见的四种情况进行解析：
1、无交点；如果二次函数与X轴无交点，则判别公式b^2-4ac0,k>0则一定与X轴无交点。
2、有一个交点；这种情况下求根公式等于0，函数解析式应该可以进行因式分解，并且是一个完全平方数，作为学生要对x+1,x-1,x+2,x-2等式子的完全平方式非常熟悉，一看就知道是完全平方式。常见的y=x^2+2x+1,或者y=x^2-2x+1都是完全平方式。
3、有两个交点；这种情况下求根公式大于0，通常情况下，二次函数都是与X轴有两个交点。这两个交点也有三种可能，第一种是一个交点在正半轴，一个交点在负半轴；第二种可能是两个都在正半轴；第三种可能是都在负半轴。
4、有交点；这个时候，一定要注意，有交点有两层含义，一层含义是有一个交点，第二层含义是有两个交点。部分同学只注意到有两个交点，疏忽有一个交点也算是有交点，犯错的原因是对题目意思没有理解。
二次函数与Y轴交点的求解方法
函数与Y轴的交点，要么在Y轴的正半轴，要么在Y轴的负半轴，还有一种特别情况，就是过原点，此时的函数解析式的常数项必是0。如果与Y轴的正半轴有交点，则常数项c大于0，如果与Y轴的负半轴有交点，则常数项c小于0。
通常在解题中，会出现这样的题型：
已知某二次函数经过（0，c)，题目中会具体地指出c的值，这个时候，可以把函数解析式y=ax^2+bx+c得c的具体值直接带入解析式中，求解更加方便。
还有根据函数经过Y轴正半轴或者负半轴，可以肯定必定过哪个象限，如果经过Y轴的正半轴，则必定经过第二象限。如果经过Y轴负半轴，则必定经过第三象限。
【变式1】（2022·福建福州·福建省福州教育学院附属中学校考模拟预测）已知抛物线与轴的交点为和，点，是抛物线上不同于，的两个点，记的面积为，的面积为，有下列结论：
①当时，；
②当时，；
③当时，；
④当时，．
其中正确结论的序号是（ ）
A．②③B．①③C．①②③④D．③
【变式2】（2022·福建漳州·统考模拟预测）在平面直角坐标系中，已知函数，，，其中a，b，c是正实数，且满足．设函数，，的图象与x轴的交点个数分别为，，，则下列说法一定正确的是（ ）
A．若，，则B．若，，则
C．若，，则D．若，，则
【变式3】（2022·山东青岛·山东省青岛实验初级中学校考模拟预测）函数（a为常数）的图象与坐标轴只有两个交点，则______．
【变式4】（2022·浙江宁波·校考模拟预测）已知关于的方程的两个根分别是，若点是二次函数的图象与轴的交点，过作轴交抛物线于另一交点，则的长为 _____．
【变式5】（2021·江苏南通·统考一模）已知抛物线y＝x2+2mx+m2﹣1（m是常数）．
(1)求该抛物线与x轴交点坐标及顶点坐标（可用含m的代数式表示）；
(2)将该抛物线先向右平移2个单位长度，再向上平移（2m﹣1）个单位长度，若平移后的抛物线与x轴没有公共点，且当x≤0时，y随x的增大而减小，求m的取值范围；
(3)已知A（1，1），B（3，1），若该抛物线与线段AB只有一个公共点，直接写出m的取值范围．
考查类型二 恒成立问题
例1 （2020·浙江嘉兴·统考中考真题）小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论：①这个函数图象的顶点始终在直线y=-x+1上；②存在一个m的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形；③点A(x1,y1)与点B(x2,y2)在函数图象上，若x12m，则y1